FreeBSD的官方文档和社区的完善程度是所有操作系统里首屈一指的水平，随便对比一下Linux的发行版CentOS、Ubuntu、Arch Linux，macOS，windows，高下立判。唯二缺点是用户少导致软件生态不如Linux（但有兼容层），且其中文资料比较匮乏，因此在这儿记录一下我使用时遇到的问题。

文章中也包含了我对RAID（主要是RAID用到的信息编码和群论）和UPnP、SMB等通用技术的理解。

zfs, ufs

Zettabyte File System

Sun开发的世界上第一个128位文件系统，理论极限是64位文件系统的10^19倍。
zpool是个很有意思的存储管理工具，存储设备都加到zpool里，另外zfs原生支持软RAID-Z。
轻度使用其实ufs就够了，所以除了ssd系统盘另外的盘我都用的ufs。关于zfs只了解了这么多。

Unix File System

FreeBSD的原生文件系统就是UFS(1969)，FreeBSD7之后才支持ZFS(2005)。
除此之外也支持Linux的EXT(Extended file system, 1992)和微软的NTFS(New Technology FileSystem, 1993)等。
跟EXT差不多，有RAID卡不需要软RAID所以基本用的都是顺手的UFS，之后再深度体验ZFS。

GROUP

相比Linux的权限管理，FreeBSD的组是个对系统管理员比较友好的东西，基本就两种操作方式
1.直接用root修改/etc/group操作groups。
2.用pw(8))，pw groupmod wheel -m myuser在某个组里添加某个用户myusesr，或者pw usermod myuser -G wheel,operator把myuser添加进多个组（-g单个组）里。
groups(1)可以直接查看某个用户所在的组，比如groups root，
我的用户在wheel operator video这几个组里。

ports, pkg

在FreeBSD上安装第三方软件一般三种方式，1.FreeBSD Ports 套件（从源代码安装）；2.packages（从预编译的二进制版本安装）；3.从网上搜资源自己编译安装。
绝大多数时候pkg install就够用了，两者各有优势，
Package Benefits

• A compressed package tarball is typically smaller than the compressed tarball containing the source code for the application.
• Packages do not require compilation time. For large applications, such as Firefox, KDE Plasma, or GNOME, this can be important on a slow system.
• Packages do not require any understanding of the process involved in compiling software on FreeBSD.

Port Benefits

• Packages are normally compiled with conservative options because they have to run on the maximum number of systems. By compiling from the port, one can change the compilation options.
• Some applications have compile-time options relating to which features are installed. For example, NGINX® can be configured with a wide variety of different built-in options.
• In some cases, multiple packages will exist for the same application to specify certain settings. For example, NGINX® is available as a nginx package and a nginx-lite package, depending on whether or not Xorg is installed. Creating multiple packages rapidly becomes impossible if an application has more than one or two different compile-time options.
• The licensing conditions of some software forbid binary distribution. Such software must be distributed as source code which must be compiled by the end-user.
• Some people do not trust binary distributions or prefer to read through source code in order to look for potential problems.
• Source code is needed in order to apply custom patches.

大体上package就是默认推荐安装，port是自定义安装，可以自己修改源代码。

packages

关于pkg，以wireshark为例常用的命令有几个，
pkg search wireshark 搜索，
pkg install wireshark 安装，
pkg remove wireshark 删除，
关于更新软件，
pkg upgrade 会更新所有的包，但关于做过自定义配置的package你可能并不想全部更新，比如wireshark遇到问题我用upgrade解决后，v2ray回到原先版本又报panic，另外qbt升级后不再继承web-ui要单独运行nox。这时，可以使用pkg-lock(8)，
pkg lock -a 锁定全部packages，这时被锁定的不会受reinstallation, modification or deletion影响，然后
pkg unlock wireshark 解锁需要更新的几个特定packages，再运行upgrade就可以对特定的软件用pkg更新了。

btw，pkg-remove(8) and pkg-delete(8) are the same thing (remove is an alias for delete).

ports

ports安装软件的基本流程，
cd /usr/ports/net/wireshark 到需要安装的软件的源代码路径，
make install clean 一步完成 make、 make install 和 make clean 这三个分开的步骤的工作。
ports使用fetch(1)下载，设置代理也是对fetch配置环境变量，详细的fetch(3)。
顺带一提，FreeBSD里下载某个文件也是fetch url即可。

注意，尽量别用make deinstall/reinstall，我在解决下面wireshark那个动态库的问题时，因为操作自己下的新版本误用了deinstall/reinstall，把很多包都误卸载了，我推测是因为这个命令会卸载Makefile里的所有包，包括依赖，pkg remove就只会卸载指定包。

Yeah, “make deinstall” uses the information in the port Makefile and pkg-plist to see what to remove. If the version in the Makefile is not identical to the installed version, files can be left behind or accidentally deleted.

“pkg_delete” uses the information in /var/db/pkg, which corresponds to what’s actually on the disk.

“make deinstall” and “make reinstall” should really only be used for testing. “pkg_delete” and “make install” are better, more reliable tools.
phoenix也提到除了测试时尽量不要用。

xorg, gui

跟随官方教程如果遇到xrandr的Can’t open display错误，需要先xinit，DISPLAY变量会由xinit设置(:0)，或者多尝试一下setenv DISPLAY，尽量不要Xorg -configure创建一个新的xorg.conf，xorg可以自动检测大部分参数。
pkg install mate
如果没有自动启动gui的话，在～下创建.xinitrc输入exec mate-session，之后就可以用xinit从cli进入gui（或者直接用exec mate-session）。

中文乱码的话可以不用下文泉驿的字体，直接在/usr/ports的Chinese里make就能解决。
MATE(马黛)的效果可以看下面ddns的那张图。

mount new disk

root@nas:/ # geom part list
root@nas:/ # gpart create -s GPT ada0
The partition scheme is created, and then a single partition is added. To improve performance on newer disks with larger hardware block sizes, the partition is aligned to one megabyte boundaries:
root@nas:/ # gpart add -t freebsd-ufs -a 1M ada0
Depending on use, several smaller partitions may be desired. See gpart(8) for options to create partitions smaller than a whole disk.
The disk partition information can be viewed with gpart show:
root@nas:/home/V2beach/Desktop # gpart show ada0
=>       40  976773088  ada0  GPT  (466G)
         40       2008        - free -  (1.0M)
       2048  976771072     1  freebsd-ufs  (466G)
  976773120          8        - free -  (4.0K)
A file system is created in the new partition on the new disk:
root@nas:/ # newfs -U /dev/ada0p1
/dev/ada0p1: 476939.0MB (976771072 sectors) block size 32768, fragment size 4096
	using 763 cylinder groups of 625.22MB, 20007 blks, 80128 inodes.
	with soft updates
super-block backups (for fsck_ffs -b #) at:
 192, 1280640, 2561088, 3841536, 5121984, 6402432, 7682880, 8963328, 10243776, ...
 An empty directory is created as a mountpoint, a location for mounting the new disk in the original disk’s file system:
root@nas:/ # mkdir /newdisk
root@nas:/ # mount /dev/ada0p1 /newdisk
root@nas:/ # chmod 777 /newdisk

以上是按照https://docs.freebsd.org/en/books/handbook/disks/的做法。
但是这样挂载的硬盘在重启后就不在挂载点上了，而是跑到了/media下面，想一直mount在mount point上就要手动写入fstab，

root@nas:/ # vim /etc/fstab
# Device                Mountpoint      FStype  Options         Dump    Pass#
/dev/gpt/efiboot0               /boot/efi       msdosfs rw              2       2
/dev/nvd0p3             none    swap    sw              0       0
/dev/ada0p1     /newdisk        ufs     rw      2       2
/dev/mfid0p1    /RAID_LSI9271_ST4000VX015       ufs     rw      2       2

proxy

直接pkg install v2ray，
在/etc/rc.conf中加入v2ray_enable=”YES”之后service v2ray start即可。
但注意，直接使用会报版本相关的错，

root@nas:/ # service v2ray start
Starting v2ray.
root@nas:/ # panic: qtls.ClientHelloInfo doesn't match

goroutine 1 [running]:
github.com/marten-seemann/qtls-go1-15.init.0()
	github.com/marten-seemann/qtls-go1-15/unsafe.go:20 +0x132

root@nas:/ # find / -name v2ray
/usr/local/bin/v2ray
/usr/local/etc/v2ray/config.json

上传FreeBSD的v2ray时不小心把macOS的v2ray删掉了，下了个新的改了MEOW.sh（sed36&新版本v2ray要跟run才运行）之后报文件损坏的错误，xattr -cr即可修复。

note: socks port 1081; http port 8001.

dlna

server

root@nas:/ # pkg install minidlna
root@nas:/ # vim /usr/local/etc/minidlna.conf
[minidlna.conf](https://man.freebsd.org/cgi/man.cgi?query=minidlna.conf)
基本只需要修改media_dir=/newdisk
echo 'minidlna_enable="YES"' >> /etc/rc.conf
service minidlna start/rescan

Some facts:

• uPNP protocol uses UDP 1900
• miniDLNA uses TCP 8200 for status web page
• miniDLNA on FreeBSD:
  • service is minidlna
  • process is minidlnad
  • configuration is /usr/local/etc/minidlna.conf
  • log file (default) is /var/log/minidlna.log
  • db directory (default) is /var/db/minidlna/
• minidlnad -R to rescan
• VLC can be used as DLNA client

client

macOS和windows都是下载VLC等支持dlna的播放器，在UPnP里可以搜索到同局域网的dlna服务器。
macOS上SMB协议速度比较慢，之后可能需要尝试NFS，尝试了。

DLNA协议集

DLNA(Digital Living Network Alliance 数字生活联盟)，根据spirespark文档，协议集包括以下部分，

这么看不太直观，对比OSI或者TCP/IP模型就能看的比较清楚，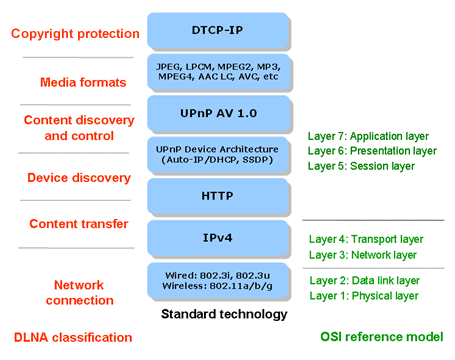

数据链路层802系列协议，网络层IP协议，传输层的TCP和UDP分别支持下面图上的应用层HTTP/UPnP协议。
其中核心是UPnP（Universal Plug and Play 通用即插即用），实现了DLNA的设备发现、控制等基本功能。

UPnP协议集

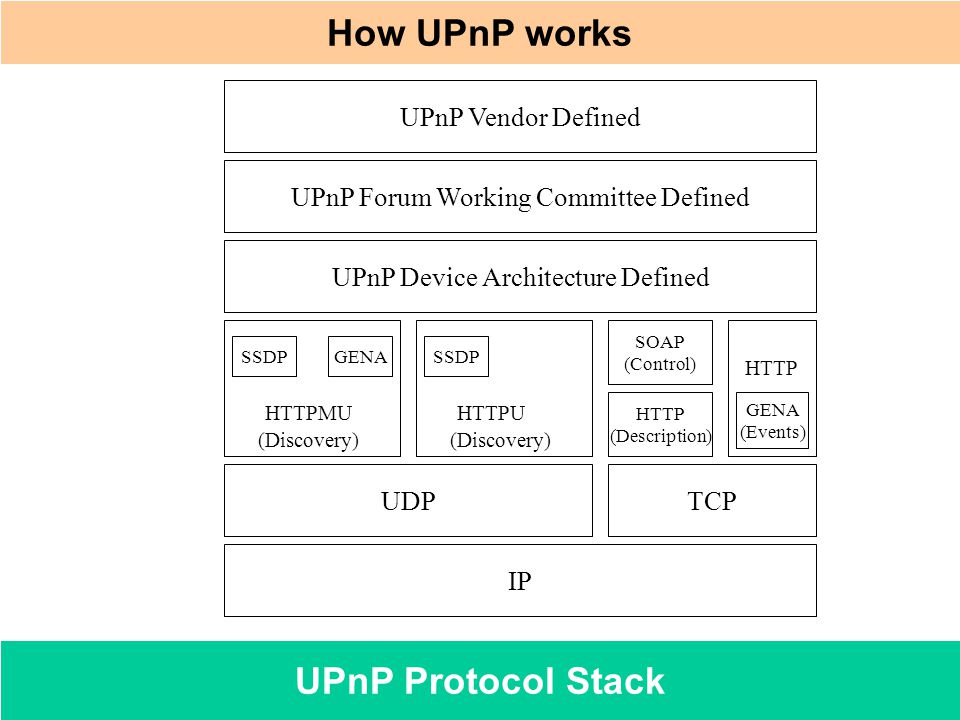
UPnP协议集又包含三个核心协议，SSDP（Simple Service Discovery Protocol 简单服务发现协议）、SOAP（Simple Object Access Protocol 简单对象访问协议）、GENA（Generic Event Notification Architecture 一般事件通知架构）。
根据维基百科的解释（概括得很好的几段我直接搬过来），

UPnP assumes the network runs IP and then leverages HTTP, on top of IP, in order to provide device/service description, actions, data transfer and event notification. Device search requests and advertisements are supported by running HTTP on top of UDP (port 1900) using multicast (known as HTTPMU). Responses to search requests are also sent over UDP, but are instead sent using unicast (known as HTTPU).
UPnP uses UDP due to its lower overhead in not requiring confirmation of received data and retransmission of corrupt packets. UPnP uses UDP port 1900 and all used TCP ports are derived from the SSDP alive and response messages.

UPnP假定网络运行着Internet Protocol并且利用IP之上的HTTP，提供设备或服务的描述、活动、数据交换和事件通知。设备发现请求由HTTPMU实现（UDP1900端口上的广播HTTP请求）；响应由HTTPU（Hypertext Transfer or Transport Protocol over UDP）实现，是单播的，也用UDP。
UPnP用UDP是因为开销较低（不需要确认收到数据且不需要重传损坏的包）。UPnP用UDP1900端口，所有用到的TCP端口都源于SSDP活跃的响应消息。

Conceptually, UPnP extends plug and play—a technology for dynamically attaching devices directly to a computer—to zero-configuration networking for residential and SOHO wireless networks.

概念上UPnP把PnP协议（把设备动态直连计算机的技术，指在電腦加上一個新的外部裝置時，能自動偵測與配置硬體資源（如I/O地址、DMA、IRQ），而不需要重新組態或手動安裝驅動程式。USB、PCIE、SATA/SAS、DVI/HDMI、Thunderbolt都是目前常用的PnP接口）扩展到简单场景的零配置无线网络。

UPnP的Control Points（CPs控制点）使用UPnP控制Controlled Devices（CDs被控制设备），Dynamic Host Configuration Protocol (DHCP) and Domain Name System (DNS) servers are optional and are only used if they are available on the network. DHCP和DNS服务器都是可选的。

UPnP的作用过程如下，

Addressing
The foundation for UPnP networking is IP addressing. Each device must implement a DHCP client and search for a DHCP server when the device is first connected to the network. If no DHCP server is available, the device must assign itself an address. The process by which a UPnP device assigns itself an address is known within the UPnP Device Architecture as AutoIP. If during the DHCP transaction, the device obtains a domain name, for example, through a DNS server or via DNS forwarding, the device should use that name in subsequent network operations; otherwise, the device should use its IP address.

1.寻址，UPnP网络的基础是IP寻址，每个设备都必须实现一个DHCP客户端，并在第一次加入网络时寻找一个DHCP服务器，如果没有可用的DHCP服务器，这个设备必须给自己分配一个地址。这个UPnP设备给自己分配地址的过程叫AutoIP。如果在一个DHCP事务（transaction）中，设备获得了一个域名（比如通过一个DNS服务器或者通过DNS转发），这个设备应该在后续的网络操作中使用这个名字，否则设备应使用它的IP地址。

Discovery
Once a device has established an IP address, the next step in UPnP networking is discovery. The UPnP discovery protocol is known as the Simple Service Discovery Protocol (SSDP). When a device is added to the network, SSDP allows that device to advertise its services to control points on the network. This is achieved by sending SSDP alive messages. When a control point is added to the network, SSDP allows that control point to actively search for devices of interest on the network or listen passively to the SSDP alive messages of devices. The fundamental exchange is a discovery message containing a few essential specifics about the device or one of its services, for example, its type, identifier, and a pointer (network location) to more detailed information.

2.发现，一个设备建立了IP地址之后，在UPnP网络里的下一步是发现。UPnP发现协议是SSDP（简单服务发现协议）。当一个设备加入网络时，SSDP允许设备向网络上的控制点通过发送SSDP活动消息以通知他的服务。当一个控制点加入网络时，SSDP允许控制点主动寻找网络上的设备或者被动监听网络上设备的SSDP活动消息。基本交换是一个包含一些关于设备或服务的重要细节的发现消息，比如它的类型、标识符或者一个指针（网络位置）指向更多细节信息。

Description
After a control point has discovered a device, the control point still knows very little about the device. For the control point to learn more about the device and its capabilities, or to interact with the device, the control point must retrieve the device’s description from the location (URL) provided by the device in the discovery message. The UPnP Device Description is expressed in XML and includes vendor-specific manufacturer information like the model name and number, serial number, manufacturer name, (presentation) URLs to vendor-specific web sites, etc. The description also includes a list of any embedded services. For each service, the Device Description document lists the URLs for control, eventing and service description. Each service description includes a list of the commands, or actions, to which the service responds, and parameters, or arguments, for each action; the description for a service also includes a list of variables; these variables model the state of the service at run time, and are described in terms of their data type, range, and event characteristics.

3.描述，在一个控制点发现了一个设备之后，控制点仍不了解设备，因此控制点要检索发现消息里提供的位置（或URL）里面的描述。UPnP设备描述是XML格式的，包含运营商特定的制造商信息，还包含一系列嵌入式服务。对于每个服务，设备描述又都会进一步提供控制、事件和服务描述的URL。每个服务描述包含一系列命令和变量。

Control
Having retrieved a description of the device, the control point can send actions to a device’s service. To do this, a control point sends a suitable control message to the control URL for the service (provided in the device description). Control messages are also expressed in XML using the Simple Object Access Protocol (SOAP). Much like function calls, the service returns any action-specific values in response to the control message.

4.控制，检索了设备描述之后，控制点会发送一些行动给一个设备的服务。控制点会向（设备描述里提供的）控制URL发送一个恰当的控制消息，控制消息用的是SOAP（简单对象访问协议），也是XML格式。服务在响应控制消息时会返回任何行动特定的值，很像函数调用。

Event Notification
Another capability of UPnP networking is event notification, or eventing. The event notification protocol defined in the UPnP Device Architecture is known as General Event Notification Architecture (GENA). A UPnP description for a service includes a list of actions the service responds to and a list of variables that model the state of the service at run time. The service publishes updates when these variables change, and a control point may subscribe to receive this information. The service publishes updates by sending event messages. Event messages contain the names of one or more state variables and the current value of those variables. These messages are also expressed in XML.

5.事件通知，UPnP网络的另一个能力是事件通知，事件通知协议是GENA（一般事件通知架构）。通过XML格式的事件消息，UPnP网络里的控制点可以随时获得设备上服务的运行时状态变量。

Presentation
The final step in UPnP networking is presentation. If a device has a URL for presentation, then the control point can retrieve a page from this URL, load the page into a web browser, and depending on the capabilities of the page, allow a user to control the device and/or view device status.

6.展示，最后一步是如果一个设备有一个展示URL，控制点会检索这个URL的页面，把页面加载到浏览器中并允许用户通过页面控制设备或者只是查看设备的状态（DLNA只允许通过默认8200端口查看状态）。

NAT traversal
One solution for NAT traversal, called the Internet Gateway Device Protocol (IGD Protocol), is implemented via UPnP. Many routers and firewalls expose themselves as Internet Gateway Devices, allowing any local UPnP control point to perform a variety of actions, including retrieving the external IP address of the device, enumerating existing port mappings, and adding or removing port mappings. By adding a port mapping, a UPnP controller behind the IGD can enable traversal of the IGD from an external address to an internal client.

一种NAT穿透的方法叫IGDP（网关设备协议）通过UPnP实现。很多路由器和防火墙会对网关设备暴露他们自己，这就让本地UPnP控制点能做很多事，包括检索一个设备的公网IP，列举它现存的端口映射，并且增删端口映射。通过增加一个端口映射，一个网关设备背后的UPnP控制者（IGD作为Controlled Device）可以让外网的网关设备穿透到内部设备。

samba

server

root@nas:/ # pkg install samba
root@nas:/ # vim /usr/local/etc/smb4.conf

[global]
workgroup          = WORKGROUP
netbios name       = freebsd-test
server string      = samba
security           = user
wins support       = yes
passdb backend     = tdbsam

# Following is the data directory you want to share.

[SMBshare]
  path = /newdisk
  valid users = V2beach
  public = no
  writable  = yes
  browsable  = yes
  read only = no
  guest ok = no
  create mask = 0755
  directory mask = 0755

root@nas:/home/V2beach/Desktop # pdbedit -a -u V2beach
new password:
retype new password:
Unix username:        V2beach
NT username:          
Account Flags:        [U          ]
User SID:             S-1-5-21-1459039941-1455980450-4236412286-1000
Primary Group SID:    S-1-5-21-1459039941-1455980450-4236412286-513
Full Name:            Hulk Leo
Home Directory:       \\FREEBSD-TEST\v2beach
HomeDir Drive:        
Logon Script:         
Profile Path:         \\FREEBSD-TEST\v2beach\profile
Domain:               FREEBSD-TEST
Account desc:         
Workstations:         
Munged dial:          
Logon time:           0
Logoff time:          Wed, 06 Feb 2036 23:06:39 CST
Kickoff time:         Wed, 06 Feb 2036 23:06:39 CST
Password last set:    Mon, 25 Sep 2023 01:34:38 CST
Password can change:  Mon, 25 Sep 2023 01:34:38 CST
Password must change: never
Last bad password   : 0
Bad password count  : 0
Logon hours         : FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF
root@nas:/home/V2beach/Desktop #

root@nas:/ #  vim /etc/rc.conf
samba_enable="YES "
samba_server_enable="YES"
root@nas:/ # service samba_server start
root@nas:/ # service samba_server status

client

windows

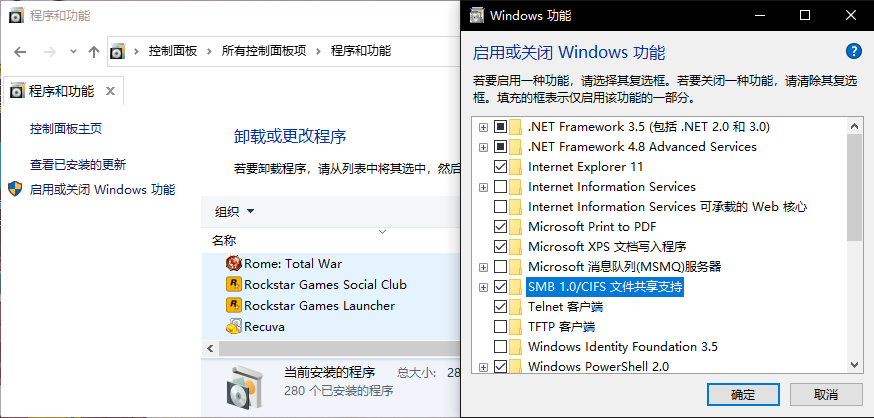
开服务之后在文件窗口输\\192.168.x.x(NAS的IP地址)\SMBshare。

macos

finder里connect to server，连smb://192.168.x.x/SMBshare。

SMB协议

Server Message Block（服务器消息块）总的来说跟DLNA相比使用上的区别有，

1.DLNA只支持AV（Audio/Video）文件共享，而SMB是任何文件的共享，可以说对“Network Attached Storage网络附加存储”来说类SMB的服务是刚需；
2.DLNA看视频比较流畅，SMB有时会卡；
3.DLNA需要支持协议的播放器（VLC），比如potplayer就不支持，而SMB在绝大多数设备上都原生支持。

Server Message Block (SMB) enables file sharing, printer sharing, network browsing, and inter-process communication (through named pipes) over a computer network. SMB serves as the basis for Microsoft’s Distributed File System implementation.
SMB relies on the TCP and IP protocols for transport. This combination allows file sharing over complex, interconnected networks, including the public Internet. The SMB server component uses TCP port 445. SMB originally operated on NetBIOS over IEEE 802.2 - NetBIOS Frames or NBF - and over IPX/SPX, and later on NetBIOS over TCP/IP (NetBT), but Microsoft has since deprecated these protocols. On NetBT, the server component uses three TCP or UDP ports: 137 (NETBIOS Name Service), 138 (NETBIOS Datagram Service), and 139 (NETBIOS Session Service).

SMB支持网络上的文件分享、打印机共享、网络浏览和进程内通信（用命名管道），SMB是微软分布式文件系统实现的基础。
SMB基于TCP/IP协议实现传输，这让SMB能进行复杂的、网络间（包括公网）的文件共享。SMB服务器组件使用TCP445端口，SMB最初在基于IEEE802.2的NetBIOS（NBF）之上实现，之后基于TCP/IP（NetBT），但微软此后放弃了这些SMB协议。NetBT实现中服务器使用UDP/137（NetBIOS 名称服务）、UDP/138（NetBIOS 数据报服务）、TCP/139（NetBIOS 会话服务）。

The NetBIOS API and the SMB protocol are generally used together as follows:

• An SMB client will use the NetBIOS API to send an SMB command to an SMB server, and to listen for replies from the SMB server.
• An SMB server will use the NetBIOS API to listen for SMB commands from SMB clients, and to send replies to the SMB client.

一个SMB客户端会通过NetBIOS API向SMB服务器发送SMB命令， 并且监听SMB服务器的响应；一个SMB服务器会通过NetBIOS API监听SMB客户端的SMB命令，并且向SMB发送响应。
但两者实际上是相互独立的，SMB可以用别的API实现设备间交流，比如用Berkeley Sockets API；NetBIOS这个接口也可以用于实现别的协议。

NFS

NFS也（还记得ZFS吗）由Sun开发，论文Design and Implementation of the Sun Network Filesystem(Sandberg, 1985)。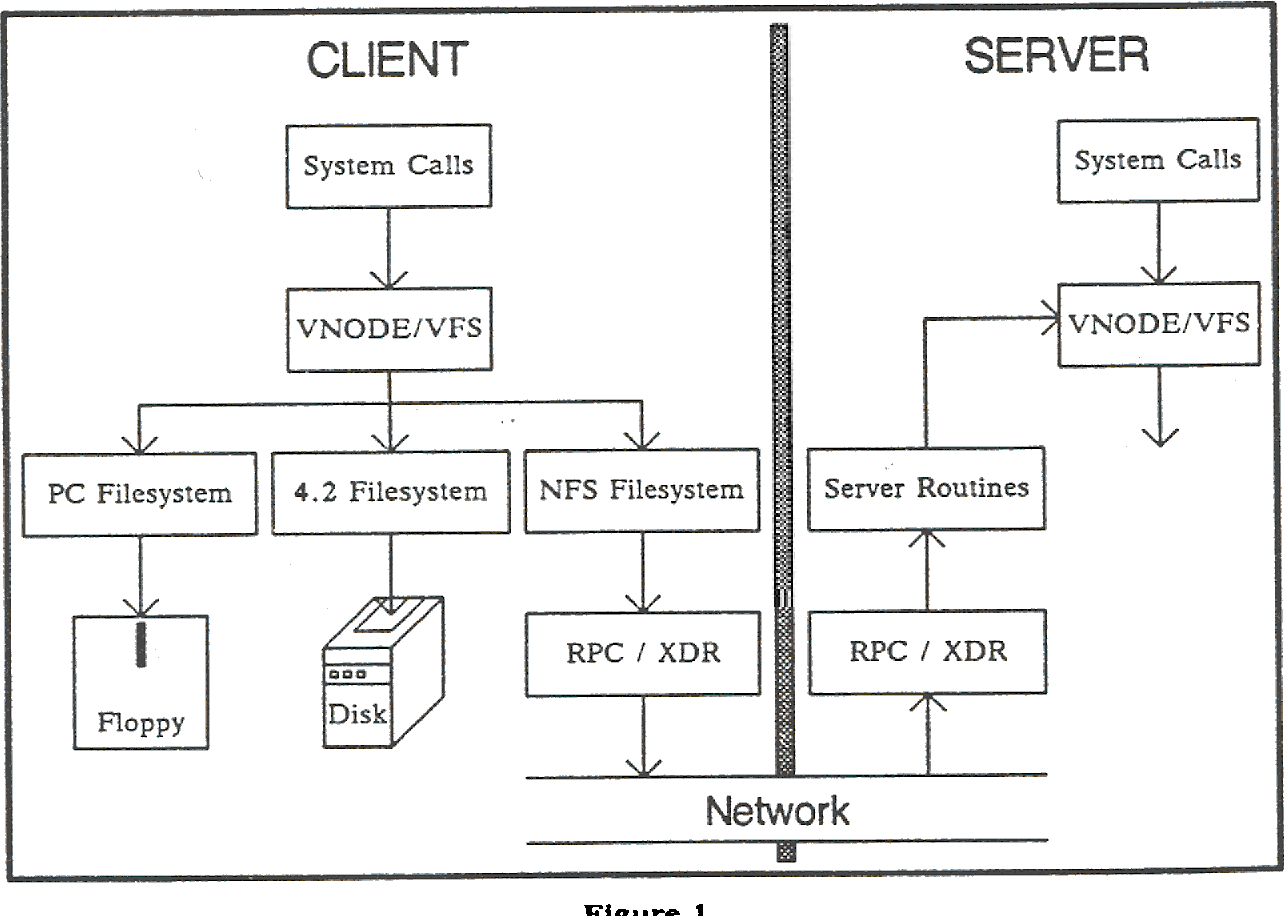

里面提到的Unix 4.2系统指的是BSD4.2，NFS(Network File System)基本上是基于RPC(Remote Procedure Call, 远程过程调用)实现的，另外XDR(External Data Representation, 外部数据表示法)指的是一种标准数据序列化格式，在OSI表示层中实现。

RPC协议

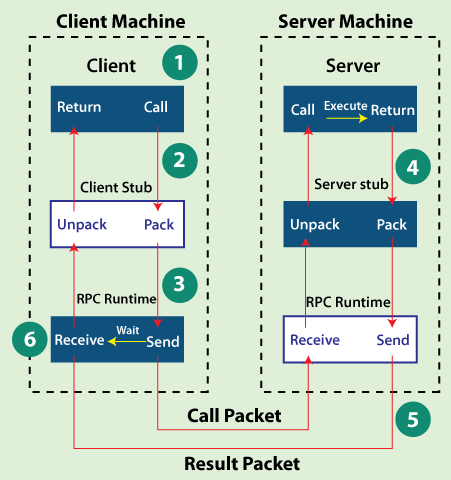
1. 客户端调用客户端stub（client stub）。这个调用是在本地，并将调用参数push到栈（stack）中。
2. 客户端stub（client stub）将这些参数包装，并通过系统调用发送到服务端机器。打包的过程叫 marshalling。（常见方式：XML、JSON、二进制编码）
3. 客户端本地操作系统发送信息至服务器。（可通过自定义TCP协议或HTTP传输）
4. 服务器系统将信息传送至服务端stub（server stub）。
5. 服务端stub（server stub）解析信息。该过程叫 unmarshalling。
6. 服务端stub（server stub）调用程序，并通过类似的方式返回给客户端。

所谓marshal（集结、结集、编码、编组、编集、安整、数据打包、列集）就是把一个对象的内存变成适合存储和发送的数据格式，类似于序列化，比如用JAXB把一个学生对象转成XML文件。
unmarshal解集，即逆过程。
序列化一个对象意味着把它的状态转化为字节流，使这个字节流能反向转化为该对象的一个副本。
术语“marshal”被Python标准库认为与“序列化”同义。但与Java相关的RFC 2713不认为二者是同义：
“marshal”一个对象意味着记录下它的状态与codebase(s)在这种方式，以便当这个marshal对象在被”unmarshalled”时，可以获得最初代码的一个副本，可能会自动装入这个对象的类定义。可以marshal任何能被序列化或远程（即实现java.rmi.Remote接口）。Marshalling类似序列化，除了marshalling也记录codebases。Marshalling不同于序列化是marshalling特别处理远程对象。
——Schema for Representing Java(tm) Objects in an LDAP Directory (RFC 2713)

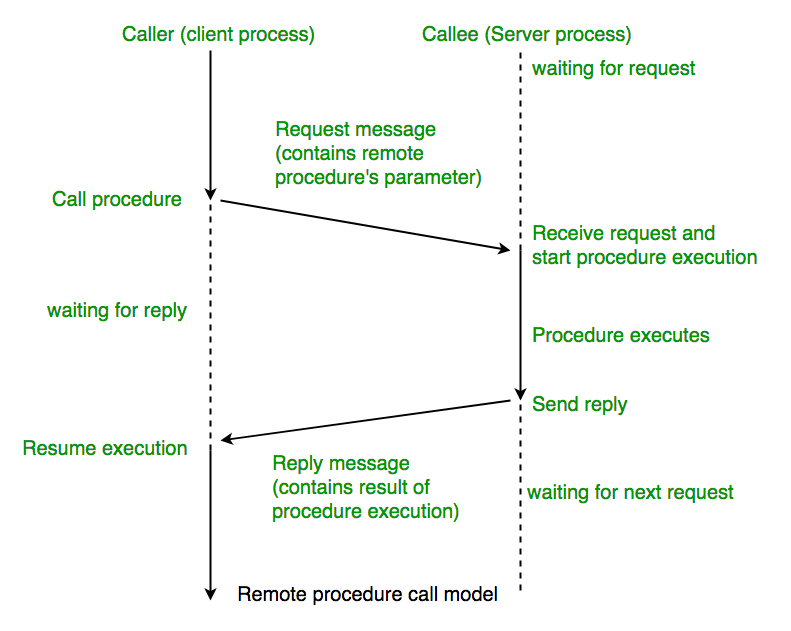
远程过程调用是一个分布式计算的客户端-服务器（Client/Server）的例子，它简单而又广受欢迎。
远程过程调用总是由客户端对服务器发出一个执行若干过程请求，并用客户端提供的参数。
执行结果将返回给客户端。

server

root@nas:/RAID_LSI9271_ST4000VX015 # rm -rf .Trash-1001/
root@nas:/RAID_LSI9271_ST4000VX015 # vim /etc/rc.conf

hostname="nas.v2beach.cn"
ifconfig_em0_ipv6="inet6 accept_rtadv"
create_args_wlan0="country CN regdomain ETSI"
local_unbound_enable="YES"
sshd_enable="YES"
moused_enable="YES"
ntpdate_enable="YES"
ntpd_enable="YES"
powerd_enable="YES"
# Set dumpdev to "AUTO" to enable crash dumps, "NO" to disable
dumpdev="AUTO"
zfs_enable="YES"
kld_list="i915kms"
dbus_enable="YES"
lightdm_enable="YES"
v2ray_enable="YES"
minidlna_enable="YES"
samba_server_enable="YES"
jail_enable="YES"
# NFS configuration
rpcbind_enable="YES"
nfs_server_enable="YES"
nfs_server_flags="-u -t -n 4"
mountd_enable="YES"
mountd_flags="-r"
"/etc/rc.conf" 27L, 642B written

root@nas:/RAID_LSI9271_ST4000VX015 # vim /etc/exports

/RAID_LSI9271_ST4000VX015 -mapall=V2beach -network 192.168.2.0 -mask 255.255.255.0                                                              
"/etc/exports" [New] 1L, 83B written

root@nas:/RAID_LSI9271_ST4000VX015 # rpcbind 
root@nas:/RAID_LSI9271_ST4000VX015 # nfsd -u -t -n 4
root@nas:/RAID_LSI9271_ST4000VX015 # mountd -r
root@nas:/RAID_LSI9271_ST4000VX015 # showmount -e 192.168.2.x
Exports list on 192.168.2.x:
/RAID_LSI9271_ST4000VX015          192.168.2.0
root@nas:/RAID_LSI9271_ST4000VX015 # cat /var/run/mountd.pid 

MacOS client

sudo mount -o nolocks,resvport,locallocks -t nfs 192.168.2.x:/RAID_LSI9271_ST4000VX015 /Users/v2beach/nas

-o后用其他的参数)也可以把nas挂载到macOS上，但跟smb速度相仿，不过似乎相对稳定，用SMB传数据断了好几次，不过也可能是路由器出问题重启了（因为断传的时候网也断了）。

iOS文件备份，sync

从照片里通过smb存储到nas太慢，改smb的配置后变更慢了，只好尝试了两个软件。
resilio sync是个P2P的网盘，潜力挺大但是跟我自动备份照片的主需求不太匹配；
photo sync相当好用，一方面速度很快而且支持的连接设备和功能都很全，另一方面我很喜欢跟iOS照片一样按天分类的功能。

Android文件备份，sync

用photosync一直报rename和null之类的错，
看了半天v2ex选用了syncthing，也是个P2P的文件传输软件，FreeBSD里可以直接用pkg install syncthing安装，Android如果没有Google Play可以从GitHub获取，相当好用。

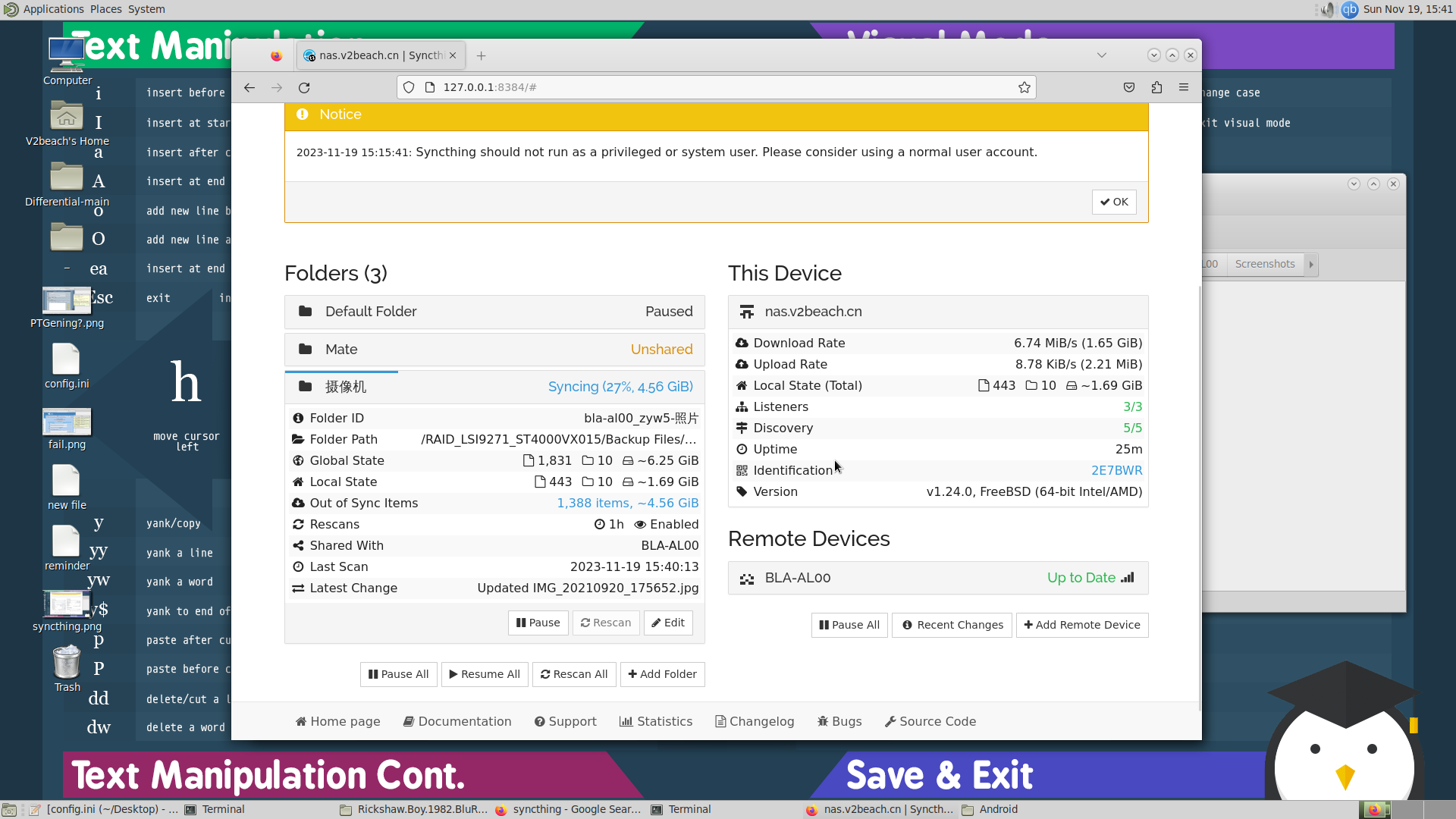相册, album, gallery

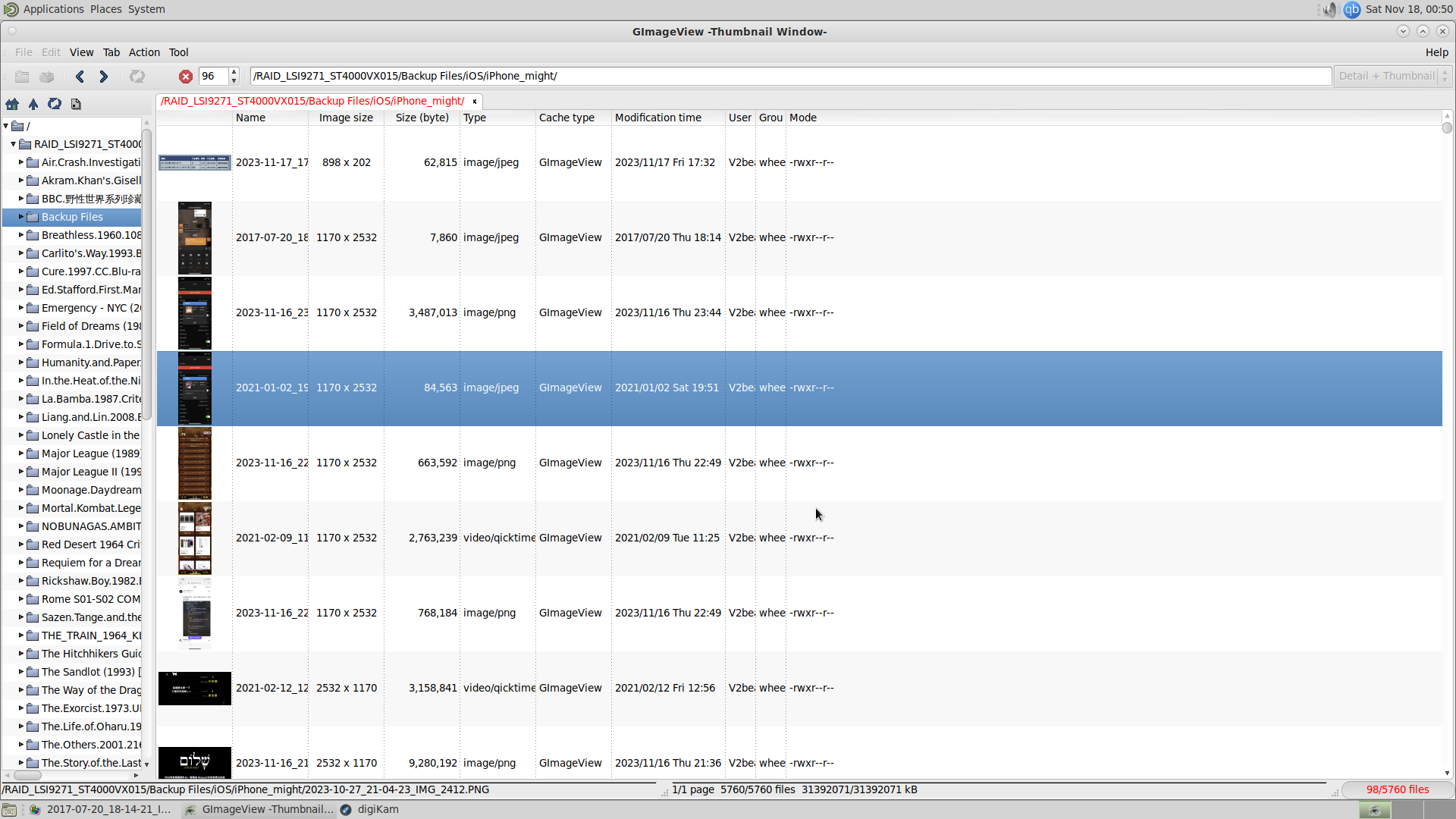
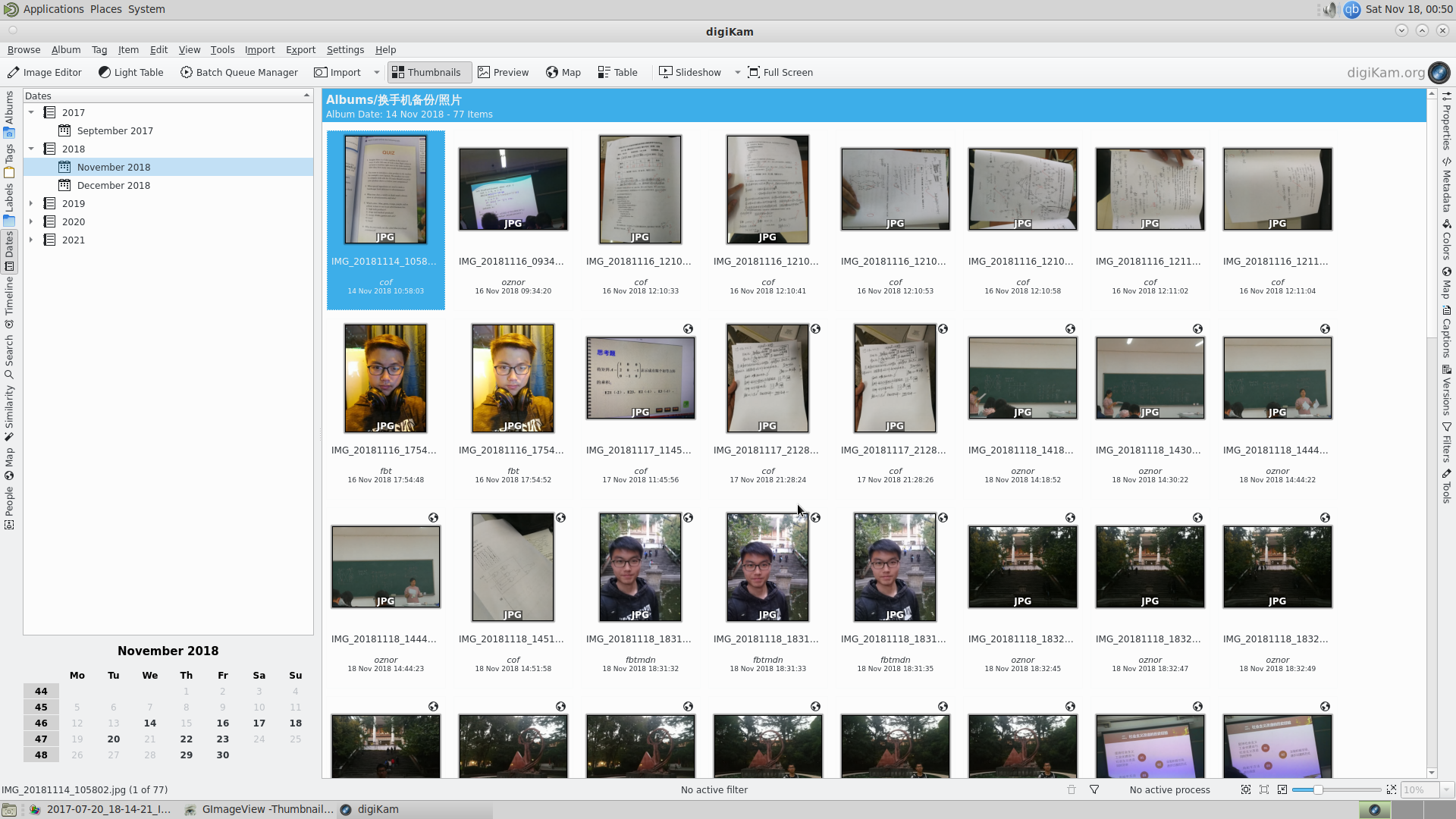
测试了很多软件，其中三个比较好用，geeqie可以批量操作图片，GImageView是相当轻量的图片管理，但没有我想要的按天分类，
最后找到了digiKam，比较重量级，不过比较符合我的需求。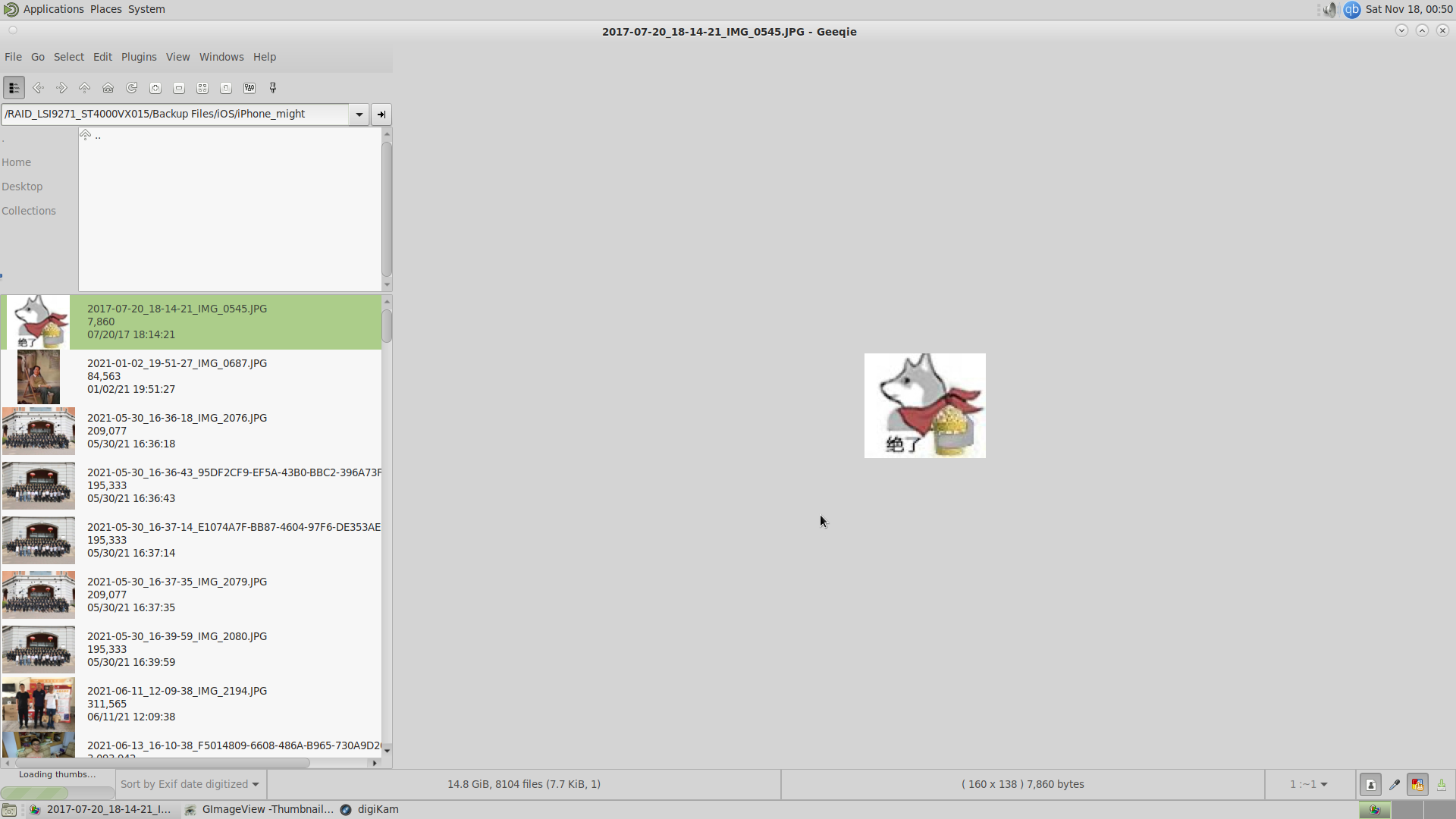

ipv6

只要是作为“网络附加存储”存在，就总有远程连接的需求，虽然只在内网使用是完全可以的。
我没有ipv4的公网ip，如果想远程访问nas还可以用ddns，但是我觉得很冗杂，其实之前我就用过向日葵和parsec，体验挺一般。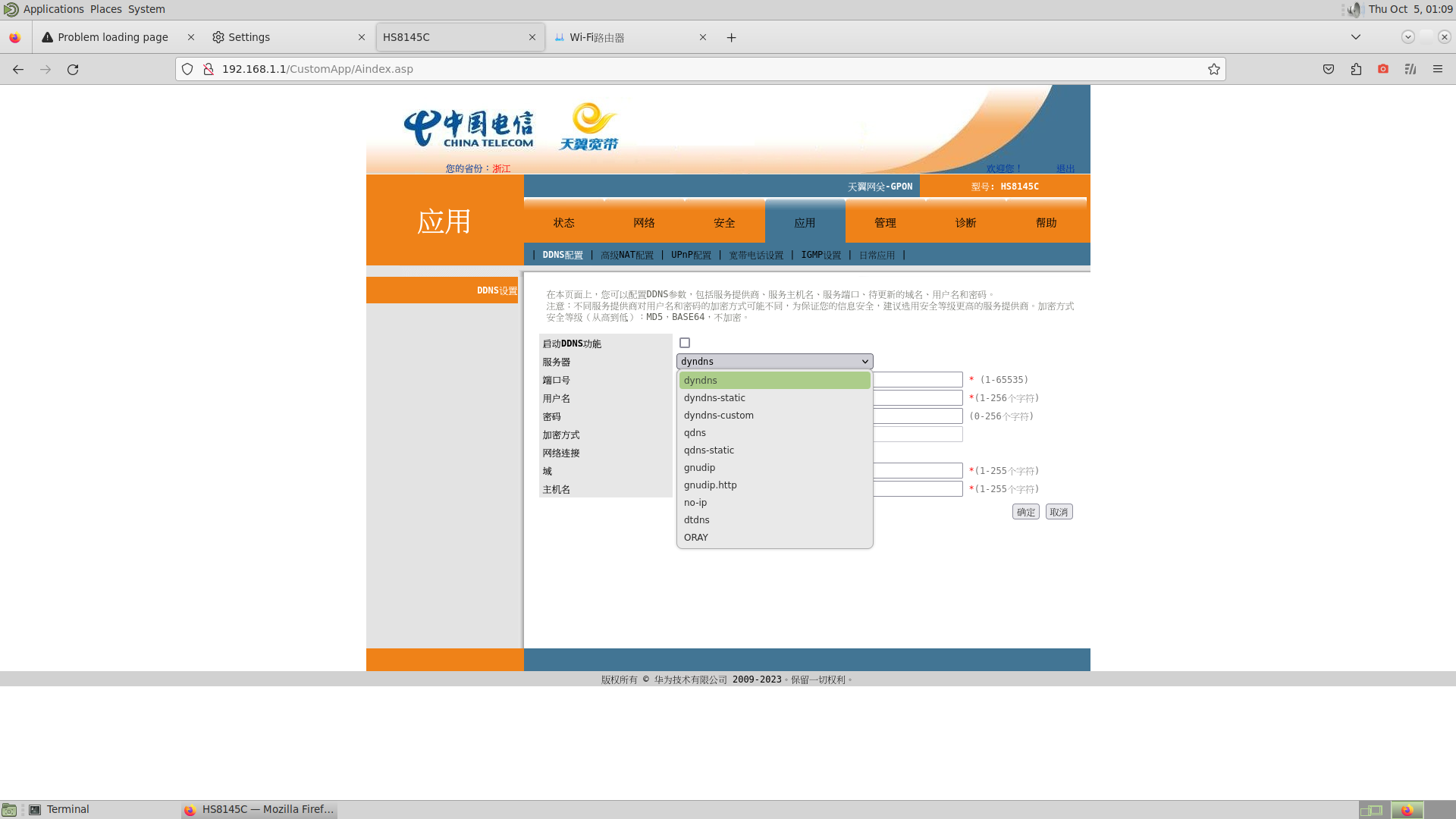

自然而然地我选择尝试给nas配一个ipv6，看到的教程里都需要光猫改桥接后用支持ipv6的路由器分配地址，所以我先鼓捣起了光猫。

一开始死活找不到复杂配置的入口，直接访问网关ip就只能访问到简化设置，后来才发现是在8080端口，但useradmin的权限也相当有限，大部分功能都配置不了，而管理员用户的密码在联网的一瞬间就变成动态分配了，这时没别的办法，只能重置光猫用默认密码进设置（telecomadmin nE7jA%5m），改桥接并开启telnet（Hw9aH%6c），但没用。
1.桥接需要路由器pppoe拨号，运营商不给宽带账户密码；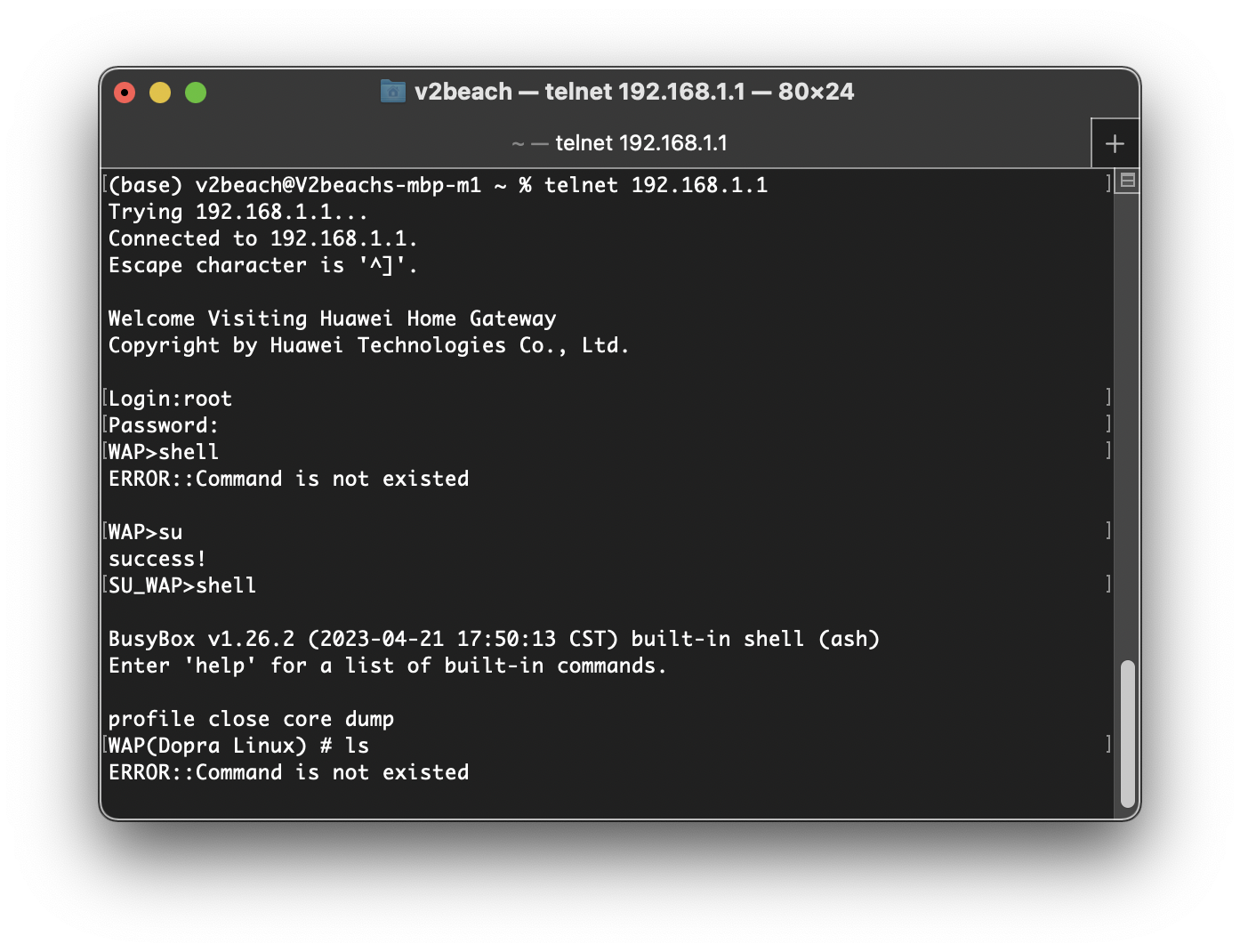

2.telnet是阉割版，几乎任何命令都用不了，用华为的enable软件使能失败，也就是说我不能通过cli获得管理员密码，每次我想设置光猫都要先捅屁股重置它。
但后来不知道是因为我改了一下出租屋的组网（把我房间的路由器直连到了光猫上，而不是再连另一个路由器），

还是我在路由器里改了ipv6的DHCP并关了防火墙，nas分配到了有效的ipv6，访问外网也可以用ipv6了，但向内的流量并不能通，局域网下是可以的。

v2ex有个很类似的问题，目前我还没解决。

jail

thick jail (classic)

a jail only needs a hostname, a root directory, an IP address, and a userland.

jail需要一个名字，一个根目录，一个IP地址和一个用户区。

IP address

jail有三种组网方式，1.Host Networking Mode (IP Sharing)跟宿主用同一个IP，2.Virtual Networks (VNET)获得独立网络栈，3.The netgraph system分别定义jail和宿主间、jails之间怎么网络交流，一般来说inherit就够用了。

userland, root directory

root@nas:/ # setenv D /usr/jail/vim-adventure
root@nas:/ # mkdir -p $D 
root@nas:/ # cd /usr/src
root@nas:/ # make buildworld 
--------------------------------------------------------------
>>> World build completed on Wed Sep 27 14:21:17 CST 2023
>>> World built in 14389 seconds, ncpu: 4
--------------------------------------------------------------
root@nas:/ # make installworld DESTDIR=$D 
root@nas:/ # make distribution DESTDIR=$D 
root@nas:/ # mount -t devfs devfs $D/dev

或者直接下载base，

fetch https://download.freebsd.org/ftp/releases/amd64/amd64/13.2-RELEASE/base.txz -o /usr/local/jails/media/13.2-RELEASE-base.txz
tar -xvf /usr/local/jails/media/13.2-RELEASE-base.txz -C /usr/jail/vim-adventure/

hostname, configuration

/etc/jail.conf或者/etc/jail.conf.d/，
比如下面我这个配置，

vim-adventure { 
  # STARTUP/LOGGING
  exec.start = "/bin/sh /etc/rc"; 
  exec.stop = "/bin/sh /etc/rc.shutdown"; 
  exec.consolelog = "/var/log/jail_console_${name}.log"; 

  # PERMISSIONS
  allow.raw_sockets; 
  exec.clean; 
  mount.devfs; 

  # HOSTNAME/PATH
  host.hostname = "${name}"; 
  path = "/usr/jail/${name}"; 

  # NETWORK
  ip4 = inherit; 
  ip6 = inherit;
  interface = em0; 
}

root@nas:/ # jexec 1 tcsh
root@nas:/ # node bin/www.js
  Listening on port 80

写这篇文章之前没多久，github上vim-adventures的逆向代码就被删除了，我本地的代码等过阵子录视频的时候传到站里。（2023-11-18）

thin jail

thin jail更轻量，官方文档给了几种实现方式，
1.Creating a Thin Jail Using OpenZFS Snapshots;
2.Creating a Thin Jail Using NullFS;
3.Creating a VNET Jail;
4.Creating a Linux Jail.
等试过哪个之后就回来补充哪个。

代码

jail基本上是chroot的加强版，官方文档讲得挺详细了，有时间再把我的理解整理出来。
最热门的容器技术docker在FreeBSD上的原生实现目前还有很多问题，但通过Linux二进制兼容层似乎可以运行。最初的FreeBSD版docker就是依赖 zfs与jail的。

wireshark

ld-elf.so.1 Undefined symbol _ZN11QToolButton13checkStateSetEv@Qt_5
根据forum，可以直接更新pkg upgrade解决问题。

Private Tracker

qbittorrent

qbt直接pkg install就能用了，我本来用的是4.5.4，但由于上面的问题，pkg upgrade完变成4.5.5，gui里没有了web-ui选项，想用webui要手动启动nox。（直接命令行qbittorrent-nox）
cli配置方法~/.config/qBittorrent/qBittorrent.conf

ptpp

虽然下架了，issue里提供的FireFox安装途径仍有效，
简单来说就是去开发者中心提交一个新add-on，选on your own提交离线的插件，不用提交源代码，很快就能过审，之后直接把xpi文件拖进浏览器就行了。

iyuu

从iyuu的repo下载源码之后简单弄下环境和配置文件就能运行了，

root@nas:/ # fetch https://github.com/ledccn/IYUUAutoReseed/archive/refs/heads/master.zip
root@nas:/ # unzip master.zip
root@nas:/ # pkg install php
root@nas:/ # vim config/config.php
root@nas:/ # php iyuu.php

ISO(BDMV)

FreeBSD不支持windows打包的ISO，dlna也读不到这些文件，其实BDMV在FreeBSD上本来就不能整体播放，我一般是在STREAM里找最大的m2ts文件播放，问题是跟常用字幕对不上。
解决方法是windows里通过SMB协议直接把BDMV和ISO拖到播放器里播放。

root@nas:/ # mdconfig -a -t vnode -f some.iso (or -u 0)
md0
root@nas:/ # mount -t cd9660 /dev/md0 /mnt
root@nas:/ # man tar | less +/9660
root@nas:/ # tar -tf/-xf file.iso
root@nas:/ # file - < /dev/md0
/dev/stdin: data
root@nas:/ # file -s /dev/md0
/dev/md0: data

PTGen, Differential

PTGen是个为PT网站上传资源提供格式化简介生成的接口，由他基于这位Rhilip的PT-help开发（也是PTPP和AutoSeed的开发者），这哥们居然也用的是Vultr。
Differential是个更简化操作的工具，是位狗家的兄弟写的。

差速器是汽车上的一种能使左、右轮胎以不同转速转动的结构。使用同样的动力输入，差速器能够输出不同的转速。就如同这个工具之于PT资源，差速器帮你使用同一份资源，输出不同PT站点需要的发种数据。

主要是需要从ports装mono。
连下载带编译需要装大几个小时（光pillow就个把小时），从官网fetch和building过程都太慢，相比预编译的packages这ports自己编译慢得离谱了。
所以还是选择package了，因为差速器dft用的是python，还要下python和python package manager。

root@nas:/usr/ports/lang/mono # make install clean (太慢)
root@nas:/usr/ports/lang/mono # make all-depends-list (太多)
root@nas:/ # pkg install mono ffmpeg mediainfo
root@nas:/ # pkg install python
The following 2 package(s) will be affected (of 0 checked):
New packages to be INSTALLED:
            python: 3.9_3,2
            python3: 3_3
Number of packages to be installed: 2
2 KiB to be downloaded.
root@nas:/ # pkg install py39-pip
root@nas:/ # pip install --no-build-isolation Differential --proxy http://127.0.0.1:8001

1. setuptools报错，明明pip list里有但检索不到，因此需要—no-build-isolation强制不装依赖。
2. 我用的图床是用Chevereto搭的imgbb。
3. rhilip的ptgen要绕过cloudflare检测，ptgen.lgto.workers.dev 则只能通过浏览器访问，也许是关闭了ICMP之类的服务，因此要在differential/plugins/base.py(/usr/local/lib/python3.9/site-packages)里（config.ini也能改）把ptgen_url改成second_ptgen_url: str的这个https://ptgen.caosen.com ，也就是手动调一下顺序（第一个报错并不会自动尝试第二个ptgen_url），或者另找一个/自己在cloudflare搭一个改上。
4. 同样的问题也出现在短网址服务上，网站用requests连不通lg.to/new，use_short_url改成false。这里是报错示例，config.ini我放在桌面上了。
5. 配完之后发现并不能自动填充，需要自行安装easy_upload和auto_feed_js，我选择的是easy_upload，需要装Tampermonkey以应用Typescript脚本，配好后目前是挺好用的。
6. 最后提一个我在FreeBSD上老犯的错，因为在CLI里我通常偷懒用root，这时运行dft是在root权限下启动firefox，会发现跟普通用户下的同一个软件不一样（插件和cookie之类的都不见了），这是因为不同用户的同一个application有不同的设置，V2beach@nas:~ % firefox或dft就好了。

问题5	配好后	问题6

GEOM, RAID

GEOM在handbook里叫模块化磁盘变换框架，FreeBSD里不用ZFS的话其实还可以用GEOM组RAID，所以在这提一嘴。
GEOM还直接支持用ggated(8)远程使用设备，不知相比SMB和DLNA效果如何，有待尝试。
然后分别记录一下各种RAID（Redundant Array of Independent Disks 容错式磁盘阵列），

RAID0, 1

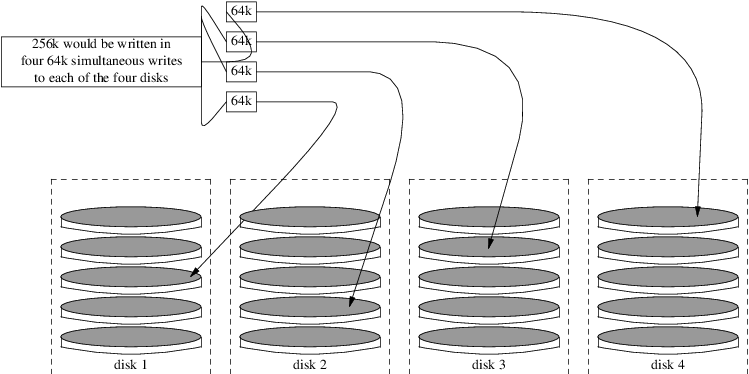
RAID0是把数据平均分散到各设备上，数据并行读写，是效率最高的RAID，也没有数据冗余，但正因如此安全性也是最差的，一个硬盘坏了可能所有数据就都不再可用了。
RAID1是镜像mirror，直接复制一份数据，我目前用的就是RAID1，硬RAID的配置很简单，在之前有提过。
RAID2用到了汉明码（Hamming Code ECC），海明码是一种ECC（Error Correction Code 纠错码），在此之前我想先回顾一下计算机网络里学过的冗余校验（Redundancy check）。

Redundancy check, Checksum, Parity bit/Check bit

Redundancy check(冗余校验)

冗余校验是一段数据中用于错误检测Error Detection和错误校正Error Correction的附加数据。
校验和是种最简单的冗余校验方式，CRC(cyclic redundancy check)循环冗余校验是经典的冗余校验方式。
以下内容主要基于维基百科，英文的比中文的要完善很多。

Checksum(校验和)

包括校验码，校验位等，其中校验码（Check digit）通常是一组数字的最后一位，由前面的数字通过某种运算得出，用以检验该组数字的正确性。比如中华人民共和国的身份证号码，一共十八位，第十八位的计算方式是，
1.计算17位数字各位数字与对应的加权因子的乘积S；
2.计算$\frac{S}{11}$的余数，$T=S\ mod\ 11$；
3.计算$\frac{12-T}{11}$的余数R，如果R=10，校验码为字母“X”；如果R≠10，校验码为数字“R”。

General topic

• Algorithm
• Check digit
• Damm algorithm
• Data rot
• File verification
• Fletcher's checksum
• Frame check sequence
• cksum
• md5sum
• sha1sum
• Parchive
• Sum (Unix)
• SYSV checksum
• BSD checksum
• xxHash

Error correction

• Hamming code
• Reed–Solomon error correction
• IPv4 header checksum

Hash functions

• List of hash functions
• Luhn algorithm
• Parity bit
• Rolling checksum
• Verhoeff algorithm

File systems

• ZFS – a file system that performs automatic file integrity checking using checksums

Related concepts

• Isopsephy
• Gematria
• File fixity

Parity bit(奇偶校验)/Check bit(校验位)

奇偶校验位Parity bit是校验和Checksum的一种，也是最简单的错误检测码Error Detecting Code。
维基百科里有个例子，

In mathematics parity can refer to the evenness or oddness of an integer, which, when written in its binary form, can be determined just by examining only its least significant bit.

在数学里parity指的是一个整数的奇偶性，当一个数被写成二进制格式时可以仅看它的least significant bit最低有效位（LSB，就是权值2^0最后那位，相对应的是M(most)SB最高有效位，就是有符号二进制采用反码或补码形式的负数里，最高的表示正负的那位，1是负数0是正数）。

The parity bit ensures that the total number of 1-bits in the string is even or odd. Accordingly, there are two variants of parity bits: even parity bit and odd parity bit. In the case of even parity, for a given set of bits, the bits whose value is 1 are counted. In the case of even parity, for a given set of bits, the bits whose value is 1 are counted. If that count is odd, the parity bit value is set to 1, making the total count of occurrences of 1s in the whole set (including the parity bit) an even number. If the count of 1s in a given set of bits is already even, the parity bit’s value is 0. In the case of odd parity, the coding is reversed. Even parity is a special case of a cyclic redundancy check (CRC), where the 1-bit CRC is generated by the polynomial x+1.

奇偶校验位确保整个二进制数的“1”有偶数个或者奇数个。因此有两种变体：偶数校验位和奇数校验位。偶数校验位是如果二进制数原本有奇数个1，那就在LSB上补一个1让整个二进制数的1有偶数个，如果原本就有偶数个1，那只需要补一个0，保持偶数个；奇数校验位反之。
偶数校验位是一种循环冗余校验CRC，一个特例，通过多项式 x + 1 得到1位CRC。

For example, suppose two drives in a three-drive RAID 5 array contained the following data:

比方说现在有个三磁盘组的RAID5，

Drive 1: 01101101
Drive 2: 11010100
01101101 XOR 11010100 = 10111001

所以，

Drive 3: 10111001

第三个磁盘存的是前两个磁盘的异或值10111001，诶？异或跟奇偶校验位是怎么扯上关系的呢？

Parity bits are written at the rate of one parity bit per n bits, where n is the number of disks in the array.
奇偶校验位按每n位（n是磁盘的个数）一个的速度被写入。

实际上磁盘1和磁盘2按位对应计算偶数校验位（even parity bit）的结果就是磁盘3存入的XOR异或值。再多一些磁盘组RAID5也是一样的偶数校验位值。

In electronics, transcoding data with parity can be very efficient, as XOR gates output what is equivalent to a check bit that creates an even parity, and XOR logic design easily scales to any number of inputs. XOR and AND structures comprise the bulk of most integrated circuitry.

在电子元件里，因为异或门XORgate的输出相当于偶数校验位，所以计算是非常高效的，并且XOR可以轻易地扩展到所有输入上，XOR异或门和AND与门构成了大多数集成电路的大部分。

RAID里奇偶校验不光做错误检测，还可以错误校正，比如RAID5的磁盘最多可以坏一个，剩下的盘可以推导出坏盘的数据，还以上面的三盘为例，

Drive 1: 01101101
Drive 2: 11010100
Drive 3: 10111001

如果盘1坏了，那Drive2 XOR Drive3 = 11010100 XOR 10111001 =
01101101 = Drive1，可以复原盘1数据。

即$A\oplus{B}=C\Rightarrow{A}\oplus{C}=B$这里简单展开一下。

operational rule of Boo-lean algebra，布尔运算律

Y = A’ · B + A · B’ = A XOR B
XOR (/ˌɛks ˈɔːr/, /ˌɛks ˈɔː/, /ˈksɔːr/ or /ˈksɔː/), EOR, EXOR, $\oplus$, $\nleftrightarrow$, $\not \equiv $. Exclusive or.

distributive law proof，(A+B)·C=A·C+B·C和A+B·C=(A+B)·(A+C)，布尔代数分配律，


Unfortunately, the only proof of a distributive law in Boolean algebra is that very law written down, since it is an independent axiom of BA which cannot be proven through another law.

根据恒等律：X ⊕ 0 = X，归零律：X ⊕ X = 0，和反演律：(A · B)’ = A’ + B’；(A + B)’ = A’ · B’（数学归纳法），得到XOR的结合律。

所以$A \oplus C = A \oplus (A \oplus B) = (A \oplus A) \oplus B = 0 \oplus B = B$，就得到了上面的公式。
本来我是觉得证分配律需要用吸收律就把证明都写了下，结果写完发现没球关系，也懒得删了就放这吧。

absorption law proof，A·(A+B)=A（对偶定律，A+A·B=A）布尔代数吸收律，
看了一下很多证明都依赖于下面的distributivity，分配律的证明又依赖于吸收律，证了个寂寞，所以我比较喜欢这位的思路，用min和max定义AND和OR。

与操作就是求0和1中的较小值，或操作就是求0和1中的较大值，所以$A·(A+B)$就变成了$min(A,max(A,B))$，
当A小于B时，当A等于B时，当A大于B时都如下所示，

两个变量比较好分类讨论，三个变量就有点麻烦了。

Hamming Code

汉明码基本上是加强版奇偶校验码，设计是十分巧妙的。

By contrast, the simple parity code cannot correct errors, and can detect only an odd number of bits in error.

对比下，简单的奇偶校验不能校正错误，而且只能检测奇数个位的错误。
汉明码会分别对数据里不同的位分组，计算多次奇偶校验码，让每一位由多个校验码控制，这样虽然增加了redundancy但大大降低了检测不出错误的概率，而且由于能定位到错的是哪一位，就有了错误校正的能力。
$2^r-r-1$长度的数据上会附加长度为r的汉明码。

以7位二进制数据1011001为例，需要4位（$2^4-4-1=7$）汉明码，选择偶校验，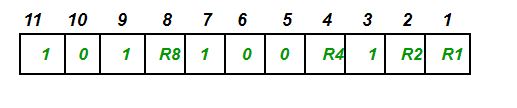

二进制第一位是1的由R1存储校验码，第3、5、7、9、11位由于有4个1，R1=3⊕5⊕7⊕9⊕11=0，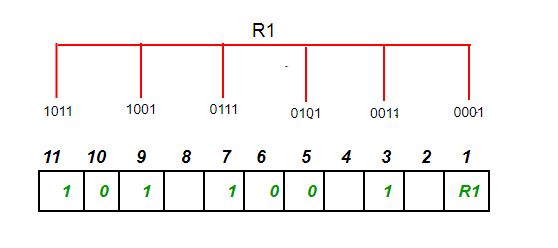

二进制第二位是1的由R2存储校验码，R2=3⊕6⊕7⊕10⊕11=1，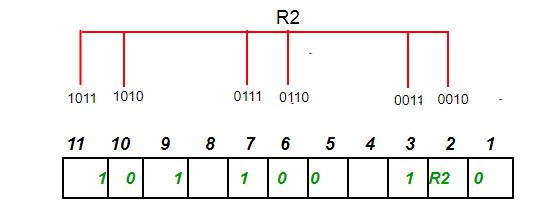

二进制第三位是1的由R4($2^{3-1}$)存储校验码，R4=1，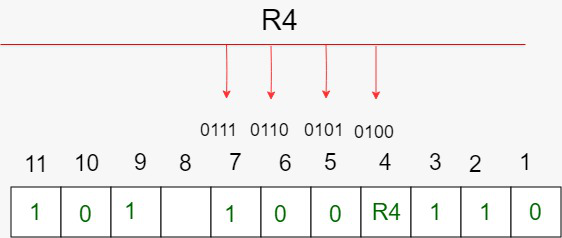

二进制第四位是1的由R8($2^{4-1}$)存储校验码，R8=9⊕10⊕11=0，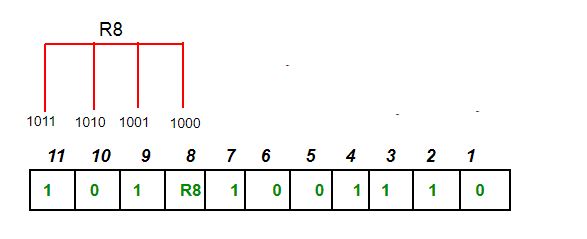

最后得到1011001被偶校验汉明编码的数据1010 1001 110。上面的校验位和数据位对应情况可以直接看下表，来自wikipedia。

群论Galois Field (i.e. Finite Field)域

上面提到过，偶数校验位实际是通过多项式 x + 1 得到1位CRC的循环冗余校验，那在探索CRC之前必须学一下GF有限域。
在学习的时候遇到了一些困难，首先是定义和性质，看得我云里雾里，分别看了维基百科、知乎和这篇文章的翻译出处Channel Codes: Classical and Modern（之后找个地方上传一下这些资源）之后，仍然没有搞清楚定义和性质的推导，不过好在对有限域的运算理解了一些，这已经足够大概理解CRC了。

以下定义将直接摘抄自Channel Codes: Classical and Modern，这本书是美籍华人Adjunct Professor林舒和William E. Ryan的著作（2009年）。

Field

一个基本概念——

Definition 2.2. Let S be a set with a binary operation ∗. The operation is said to be commutative if, given any two elements, a and b, in S, the following equality holds:
a∗b = b∗a. (2.2)
We also say that ∗ satisfies the commutative law, if (2.2) holds.

如果一个二元操作∗（不是乘法，任意的二元操作）在S上对任意元素都满足a∗b = b∗a，我们就说二元操作∗是可交换的，也说∗满足交换律。

2.3 Fields
In this section, we introduce an algebraic system with two binary operations, called a field. Fields with finite numbers of elements, called finite fields, play an important role in developing algebraic coding theory and constructing error-correction codes that can be efficiently encoded and decoded. Well-known and widely used error-correction codes in communication and storage systems based on finite fields are BCH (Bose–Chaudhuri–Hocquenghem) codes and RS (Reed–Solomon) codes, which were introduced at the very beginning of the 1960s. Most recently, finite fields have successfully been used for constructing low-density parity-check (LDPC) codes that perform close to the Shannon limit with iterative decoding.

在信道编码的2.3节中，在介绍完2.1集合和二元运算(Sets and Binary Operations)、2.2群(Groups)之后，开始讲解有两个二元运算的代数系统——域。包含有限元素的域叫做有限域（galois），有限域在代数编码理论的发展中、在构建能高效编解码的错误校正编码中扮演了重要角色。在通信和存储系统中，基于有限域的广为人知的错误校正码有BCH码、RS码，都是在六十年代早期被发明的。最近，有限域被成功地用在构建通过迭代解码、性能接近香农极限的低密度奇偶检测（LDPC）码上。

2.3.1 Definitions and Basic Concepts
Definition 2.8. Let F be a set of elements on which two binary operations, called addition ‘‘+’’ and multiplication ‘‘·,’’ are defined. F is a field under these two operations, addition and multiplication, if the following conditions (or axioms) are satisfied.

1. F is a commutative group under addition +. The identity element with respect to addition + is called the zero element (or additive identity) of F and is denoted by 0.
2. The set F\\{0} of nonzero elements of F forms a commutative group under multiplication ·. The identity element with respect to multiplication · is called the unit element (or multiplicative identity) of F and is denoted by 1.
3. For any three elements a, b, and c in F, $a·(b+c) = a·b+a·c$ The equality is called the distributive law, i.e., multiplication is distributive over addition.

定义和基本概念。设F是一个两个二元运算（加和乘）上的集合。在满足以下情况（或公理）时这个F是加和乘运算下的域，

1. F是个加法的交换群。与加法相关的恒等元（identity element）被称为F的零元或加法单位元，用0表示。
2. 集合F\\{0}（the set that contains the elements in X but not in Y is called the difference between X and Y and is denoted by X\\Y）即没有0元素的F构成了乘法的交换群。乘法相关的恒等元叫做单位元或乘法单位元，用1表示。
3. 对于F内的任意三个元素a，b，c，$a·(b+c) = a·b+a·c$满足分配律，乘法可以分配到加法上。

From the definition, we see that a field consists of two groups with respect to two operations, addition and multiplication. The group with respect to addition is called the additive group of the field, and the group with respect to multiplication is called the multiplicative group of the field. Since each group must contain an identity element, a field must contain at least two elements. Later, we will show that a field with two elements does exist. In a field, the additive inverse of an element a is denoted by ‘‘−a,’’ and the multiplicative inverse of a is denoted by ‘‘a−1,’’ provided that a ̸= 0. From the additive and multiplicative inverses of ele- ments of a field, two other operations, namely subtraction ‘‘−’’ and division ‘‘÷,’’ can be defined.
A field is simply an algebraic system in which we can perform addition, subtraction, multiplication, and division without leaving the field.

根据定义，可以发现一个域包含两个关于二元操作的群，加法和乘法。关于加法的叫做域的加法群，关于乘法的叫域的乘法群。因为每个群必须包含一个恒等元（单位元），所以一个域至少包含两个元素{0, 1}。之后会证明两个元素的域确实存在。在域中，加法的a反过来记作“-a”，乘法的a反过来记作“a-1”（a均不等于0），从这两个相反（逆运算）可以得到subtraction ‘‘−’’ 减和division ‘‘÷” 除操作。$a − b \triangleq a + (−b)$，很明显a-a=0；$a ÷ b \triangleq a · (b−1)$，很明显a÷a=1。
域就是可以在域中的任意元素上做加减乘除运算，结果仍在域内的代数系统。

Definition 2.9. The number of elements in a field is called the order of the field. A field with finite order is called a finite field.
Definition 2.10. Let F be a field. A subset K of F that is itself a field under the operations of F is called a subfield of F. In this context, F is called an extension field of K. If K ̸= F, we say that K is a proper subfield of F. A field containing no proper subfields is called a prime field.
Definition 2.11. Let F be a field and 1 be its unit element (or multiplicative identity). The characteristic of F is defined as the smallest positive integer λ such that $\sum_{i=1}^\lambda 1=\underbrace{1+1+\cdots+1}_\lambda=0$ where the summation represents repeated applications of addition + of the field. If no such λ exists, F is said to have zero characteristic, i.e., λ = 0, and F is an infinite field.
Theorem 2.4. The characteristic λ of a finite field is a prime.

定义，域里元素的数量叫做域的阶order，阶数有限的域叫有限域。
定义，设F是一个域，F的子集K如果是满足F的操作的域那就叫F的子域。如果K不等于F，K就是一个恰当的子域。一个不包含任何恰当子域的域就叫素数域。
定义，设F是一个域而且1是乘法单位元，F的特征characteristic被定义为满足公式 $\sum_{i=1}^\lambda 1=\underbrace{1+1+\cdots+1}_\lambda=0$ 的最小正整数λ，其中的累加是重复域F里的加法操作。如果不存在这样的λ，F被称作有0特征，即λ=0且F是一个无线域。
定理，有限域的特征λ是一个素数。

构造扩展域（extenstion field）所需的不可约多项式（Irreducible Polynomial），本原多项式（Primitive Polynomial），还有群（Groups）论的概念之后再细讲。
重要的是下面的这几段，关于有限域和有限域上的多项式——

Finite Fields

2.3.2 Finite Fields
The rational-, real- and complex-number fields are infinite fields. In error-control coding, both theory and practice, we mainly use finite fields.
Let p be a prime number. In Section 2.2.2, we have shown that the set of inte- gers, {0, 1, . . ., p − 1}, forms a commutative group under modulo-p addition $\boxplus$. We have also shown that the set of nonzero elements, {1, 2, . . ., p − 1}, forms a commutative group under modulo-p multiplication $\boxdot$. Following the definitions of modulo-p addition and multiplication and the fact that real-number multiplication is distributive over real number addition, we can readily show that the modulo-p multiplication is distributive over modulo-p addition. Therefore, the set of integers, {0, 1, . . ., p − 1}, forms a finite field GF(p) of order p under modulo-p addition and multiplication, where 0 and 1 are the zero and unit elements of the field, respectively. The following sums of the unit element 1 give all the elements of the field:
$1, \quad \sum_{i=1}^2 1=2, \quad \sum_{i=1}^3 1=1 \boxplus 1 \boxplus 1=3, \quad \ldots, \quad \sum_{i=1}^{p-1} 1=p-1, \quad \sum_{i=1}^p 1=0$
Since p is the smallest positive integer such that $\sum_{i=1}^p 1=0$, the characteristic of the field is p. The field contains no proper subfield and hence is a prime field.

有理数、实数和复数域都是无限域。在错误控制编码的理论和实践中，我们常用的都是有限域。
设p是一个素数（不是素数的待会儿会讨论到），在群的小节里这本书讨论过，

1. 整数集{0, 1, . . ., p − 1}构成模p加法（modulo-p addition $\boxplus$）的交换群，
2. 还有无零元素集合{1, 2, . . ., p − 1}构成模p乘法（modulo-p multiplication $\boxdot$）交换群。
3. 模p就是运算后对p取模，比如modulo-7的$1 \boxplus 9 = 10\ mod\ 7 = 3$。根据模运算定义和实数中乘法满足对加法的分配律的基本事实，可以证明模p乘法对模p加法也满足分配率。

三个条件都满足了，这个{0, 1, . . ., p − 1}就构成了阶数为p的有限域GF(p)，0和1分别是域上的加法单位元和乘法单位元。
接下来的累加就是域里的所有元素：
$1, \quad \sum_{i=1}^2 1=2, \quad \sum_{i=1}^3 1=1 \boxplus 1 \boxplus 1=3, \quad \ldots, \quad \sum_{i=1}^{p-1} 1=p-1, \quad \sum_{i=1}^p 1=0$，
因为p是最小的满足$\sum_{i=1}^p 1=0$的正整数，因此p是这个域的特征（即λ=p）。这个域不包含任何恰当的子域因此是一个素数域。

需要记住特征就是要用来模运算的数，阶数是域的元素数。

Example 2.8. Consider the special case for which p = 2. For this case, the set {0, 1} under modulo-2 addition and multiplication as given by Tables 2.6 and 2.7 forms a field of two elements, denoted by GF(2).
Note that {1} forms the multiplicative group of GF(2), a group with only one element. The two elements of GF(2) are simply the additive and multiplicative identities of the two groups of GF(2). The additive inverses of 0 and 1 are themselves. This implies that 1 − 1 = 1 + 1. Hence, over GF(2), subtraction and addition are the same. The multiplicative inverse of 1 is itself. GF(2) is commonly called a binary field, the simplest finite field. GF(2) plays an important role in coding theory and is most commonly used as the alphabet of code symbols for error-correction codes.

GF(2)

关于CRC要用到的GF(2)，正好书里有个例子。
p=2的时候，在modulo-2加和乘操作下的集合{0,1}结果如下，

构成了一个包含两个元素的域，记为GF(2)。
{1}构成了GF(2)的乘法群，只有一个元素的群。GF(2)的两个元素就是GF(2)的两个群的加法单位元和乘法单位元。0和1的加法就是减法的结果，如1-1=1+1。因此，在GF(2)上的加法addition和减法subtraction操作是一样的，1的乘法的相反（逆运算）也是它自己，1乘1等于1除1。GF(2)通常被叫做二元域，也是最简单的有限域。GF(2)在编码理论里扮演了重要角色，并最常被用于ECC的编码符号字母表。
同理可以算出来在GF(5)上的modulo-5运算结果，两个对称矩阵。这里原书写错了。

现在讨论一下阶数不是素数的域。

We have shown that, for every prime number p, there exists a prime field GF(p). For any positive integer m, it is possible to construct a Galois field $GF(p^m)$ with $p^m$ elements based on the prime field GF(p) and a root of a special irreducible polynomial with coefficients from GF(p). This will be shown in a later section. The Galois field $GF(p^m)$ contains GF(p) as a subfield and is an extension field of GF(p). A very important feature of a finite field is that its order must be a power of a prime. That is to say that the order of any finite field is a power of a prime.

对素数p，都有一个素数域GF(p)。对任何正整数m，都可以构建一个基于素数域GF(p)的包含$p^m$个元素的有限域$GF(p^m)$，和一个由GF(p)构成系数的特殊不可约多项式的根。（之后的章节才继续讨论，这个我在本文也不展开了。）有限域$GF(p^m)$包含子域GF(p)，是一个GF(p)的扩展域。有限域一个很重要的特性是阶数一定要是素数的幂，任何有限域的阶数都是素数的幂。

Definition 2.12. Let a be a nonzero element of a finite field GF(q). The smallest positive integer n such that $a^n = 1$ is called the order of the nonzero field element a.
Theorem 2.5. Let a be a nonzero element of order n in a finite field GF(q). Then the powers of a, $a^n=1, a, a^2, \ldots, a^{n-1}$ form a cyclic subgroup of the multiplicative group of GF(q).
Theorem 2.6. Let a be a nonzero element of a finite field GF(q). Then $a^{q−1} = 1$.
Theorem 2.7. Let n be the order of a nonzero element a in GF(q). Then n divides q − 1.
Definition 2.13. A nonzero element a of a finite field GF(q) is called a primitive element if its order is q − 1. That is, $a^{q−1} = 1,a,a2, …,a^{q−2}$ form all the nonzero elements of GF(q).

定义，设a是有限域GF(q)的非零元素，能使$a^n = 1$的最小的正整数n叫做非零域元素a的阶。
定理，设a是阶为n的有限域GF(q)上的非零元素，a的幂构成了GF(q)乘法群的一个循环子群。
定理，设a是有限域GF(q)的非零元素，则$a^{q−1} = 1$。
定律，设n是有限域GF(q)上非零元素a的阶，那么n能整除q-1即(q-1) mod n = 0。比如GF(5)上2的阶是4，$2^4=16\ mod\ 5 = 1$，4 mod 4 = 0。证明都在书上，我就不贴了。
定义，有限域GF(q)的非零元素a如果阶是q - 1则被称作本原元。即$a^{q−1} = 1,a,a2, …,a^{q−2}$构成了GF(q)的所有非零元素。

Polynomials over Finite Fields

2.5 Polynomials over Finite Fields
In this section, we consider polynomials with coefficients from a finite field GF(q), which are used in error-control coding theory. A polynomial with one variable (or indeterminate) X over GF(q) is an expression of the following form:
$a(X) = a_0 + a_1X + …, a_nX^{n}$
where n is a non-negative integer and the coefficients $a_i$, 0 ≤ i ≤ n, are elements of GF(q). The degree of a polynomial is defined as the largest power of X with a nonzero coefficient. For the polynomial a(X) above, if $a_n \neq 0$, its degree is n; if $a_n = 0$, its degree is less than n. The degree of a polynomial $a(X) = a_0$ with only the constant term is zero. We use the notation deg(a(X)) to denote the degree of polynomial a(X). A polynomial is called monic if the coefficient of the highest power of X is 1 (the unit element of GF(q)). The polynomial whose coefficients are all equal to zero is called the zero polynomial and denoted by 0.

在这里我们只考虑在错误控制编码理论中使用的，使用有限域GF(q)的元素作为系数的多项式。一个GF(q)上的只有一个变量X的多项式形式如$a(X) = a_0 + a_1X + …, a_nX^{n}$，n是非负整数，系数$a_i$是GF(q)的元素。多项式的阶被定义为非零系数的X的最大的幂次（不太喜欢把域的阶order和多项式的阶degree写成一样，所以之后都用英文）。对于前面的多项式a(X)，如果$a_n \neq 0$，degree就是n，如果$a_n = 0$，degree就小于n。只有一个常数项的多项式$aX = a_0$的degree是0。我们使用deg(a(X))来表示a(X)的degree。当X最高幂次是1时多项式被称为首一多项式（即GF(q)的乘法单位元），如果多项式的所有系数都是0那就叫0多项式并且用0表示。

接下来分别说一下多项式的四则运算。The arithmetic of polynomials is governed by familiar rules, such as addition, subtraction, multiplication, and division.

对于这样两个多项式，$a(X)=a_{0}+a_{1} X+\cdots+a_{n} X^{n}, \quad b(X)=b_{0}+b_{1} X+\cdots+b_{m} X^{m}$——

Addition

Multiplication

$a(X) \cdot b(X)=c_{0}+c_{1} X+\cdots+c_{k} X^{k}+\cdots+c_{n+m} X^{n+m}$
$c_{k}=\sum_{\substack{i+j=k, 0 \leq i \leq n, 0 \leq j \leq m}} a_{i} \cdot b_{j}$

we can readily verify that the polynomials over $\operatorname{GF}(q)$ satisfy the following conditions.

1. Associative laws. For any three polynomials $a(X), b(X)$, and $c(X)$ over $\mathrm{GF}(q)$,

1. Commutative laws. For any two polynomials $a(X)$ and $b(X)$ over $\operatorname{GF}(q)$,

1. Distributive law. For any three polynomials $a(X), b(X)$, and $c(X)$ over $\mathrm{GF}(q)$,

In algebra, the set of polynomials over $\operatorname{GF}(q)$ under polynomial addition and multiplication defined above is called a polynomial ring over $\mathrm{GF}(q)$.

Subtraction

Subtraction of $b(X)$ from $a(X)$ is carried out as follows:

where $a_{i}-b_{i}=a_{i}+\left(-b_{i}\right)$ is carried out in $\operatorname{GF}(q)$ and $-b_{i}$ is the additive inverse of $b_{i}$.

Division

Definition 2.19. A set $\mathcal{R}$ with two binary operations, called addition + and multiplication $\cdot$, is called a ring, if the following axioms are satisfied.

1. $\mathcal{R}$ is a commutative group with respect to + .
2. Multiplication “.” is associative, i.e., $(a \cdot b) \cdot c=a \cdot(b \cdot c)$ for all $a, b, c \in \mathcal{R}$.
3. The distributive laws hold: for $a, b, c \in \mathcal{R}, a \cdot(b+c)=a \cdot b+a \cdot c$ and $(b+c) \cdot a=b \cdot a+b \cdot a$.

The set of all polynomials over $\operatorname{GF}(q)$ defined above satisfies all three axioms of a ring. Therefore, it is a ring of polynomials. The set of all integers under real addition and multiplication is a ring. For any positive integer $m \geq 2$, the set $\mathcal{R}=$ $\{0,1, \ldots, m-1\}$ under modulo- $m$ addition and multiplication forms a ring (the proof is left as an exercise). In Section 2.3, it was shown that, if $m$ is a prime, $\mathcal{R}=$ $\{0,1, \ldots, m-1\}$ is a prime field under modulo- $m$ addition and multiplication.

定义，如果一个有两个二元运算加+和乘·的集合$\mathcal{R}$叫做一个环Ring，要以下几个公理。

1. $\mathcal{R}$是一个加法的交换群。
2. 集合的任意元素间的乘法满足结合律。
3. 集合的任意元素间的运算满足分配率。

GF(q)的所有多项式的集合满足以上三个环的功力，因此GF(q)的所有多项式是一个多项式环。所有实数整数的加法和乘法是一个环。对于任意的正整数$m \geq 2$，在modulo-m加法和乘法下的集合$\mathcal{R}= \{0,1, \ldots, m-1\}$构成一个环。在上面讨论过，如果m是一个素数，$\mathcal{R}= \{0,1, \ldots, m-1\}$就是一个modulo-m加法和乘法运算下的素数域。

（这里简单提一下，在抽象代数里最先学群论，因为群的概念最大，环次之，域最小，一个环一定是一个群，一个域一定是一个环，所谓环可能指的是域里的运算始终指回域本身的这种现象，知乎有很多有趣的解释比如ring其实指团伙。）

Let $a(X)$ and $b(X)$ be two polynomials over $\operatorname{GF}(q)$. Suppose that $b(X)$ is not the zero polynomial, i.e., $b(X) \neq 0$. When $a(X)$ is divided by $b(X)$, we obtain a unique pair of polynomials over $\mathrm{GF}(q), q(X)$ and $r(X)$, such that

$a(X)=q(X) \cdot b(X)+r(X)$where $0 \leq \operatorname{deg}(r(X))<\operatorname{deg}(b(X))$ and the polynomials $q(X)$ and $r(X)$ are called the quotient and remainder, respectively. This is known as Euclid’s division algorithm. The quotient $q(x)$ and remainder $r(X)$ can be obtained by ordinary long division of polynomials. If $r(X)=0$, we say that $a(X)$ is divisible by $b(X)$ (or $b(X)$ divides $a(X))$.

$a(X)=q(X) \cdot b(X)+r(X)$其中$0 \leq \operatorname{deg}(r(X))，<\operatorname{deg}(b(X))$，多项式$q(X)$和$r(X)$分别被称为商和余，即欧几里得除法，$q(X)$和$r(X)$可以由多项式的长除算得。如果$r(X)$，我们就说$b(X)$整除$a(X)$，即$a(X)$ mod $b(X)$ = 0。
除法比较复杂所以演算一个书上的例子。

Example 2.13. Let $a(x)=3+4 X+X^{4}+2 X^{5}$ and $b(X)=1+3 X^{2}$. Suppose we divide $a(X)$ by $b(X)$. Using long division,

定理和性质就不再讨论了，理解CRC需要的知识现在都具备了。

Cyclic Redundancy Check

Introduction

A cyclic redundancy check (CRC) is an error-detecting code commonly used in digital networks and storage devices to detect accidental changes to digital data. Blocks of data entering these systems get a short check value attached, based on the remainder of a polynomial division of their contents.
CRCs are so called because the check (data verification) value is a redundancy (it expands the message without adding information) and the algorithm is based on cyclic codes. CRCs are popular because they are simple to implement in binary hardware, easy to analyze mathematically, and particularly good at detecting common errors caused by noise in transmission channels. Because the check value has a fixed length, the function that generates it is occasionally used as a hash function.

循环冗余校验是一个通常用于数字的网络和存储设备的错误校验码，来检测偶然的数据变化。根据某个多项式和数据内容做除法的余数，进入这些系统的数据块会被附加一个短的校验值。
循环冗余校验这个名字来自于，1.这个附加的校验值是冗余的（扩增了消息但没有增加信息）；2.算法基于循环码。CRCs由于易于在二进制硬件上实现、易于从数学上分析并且在检测常见的、由传输通道中的噪声造成的错误时尤其有效而被广泛使用。由于校验值是固定长度的，生成校验值的函数偶尔被用作哈希函数。

Specification of a CRC code requires definition of a so-called generator polynomial. This polynomial becomes the divisor in a polynomial long division, which takes the message as the dividend and in which the quotient is discarded and the remainder becomes the result. The important caveat is that the polynomial coefficients are calculated according to the arithmetic of a finite field, so the addition operation can always be performed bitwise-parallel (there is no carry between digits).
In practice, all commonly used CRCs employ the finite field of two elements, GF(2). The two elements are usually called 0 and 1, comfortably matching computer architecture.

CRC码需要定义一个生成多项式。这个多项式作为多项式长除的除数，消息本身作为被除数，商被舍弃而余数作为结果。一个重要的警告是，多项式系数是根据有限域的运算方式计算的，因此加法运算始终可以按位并行执行（数字之间没有进位，因为进位的要被模运算消除掉）。
在实践中所有常用的循环冗余检测都基于两个元素的有限域GF(2)，这两个元素通常是0和1，跟计算机架构很舒服地匹配了。

CRCs are specifically designed to protect against common types of errors on communication channels, where they can provide quick and reasonable assurance of the integrity of messages delivered. However, they are not suitable for protecting against intentional alteration of data.
an attacker can edit a message and recompute the CRC without the substitution being detected.
unlike cryptographic hash functions, CRC is an easily reversible function, which makes it unsuitable for use in digital signatures.

CRC是为了保护常见的通信通道的错误被特别设计的，可以快速地确保消息传递的完整。但是CRC对于有意修改的数据是不适用的。攻击者可以修改一个消息并且重新计算CRC（知道固定的多项式）并不会被检测到替换。
CRC不像密码学哈希函数，CRC很容易翻过来计算，所以不能用于数字签名。

Computation, modulo-2 division(模二除法)

为什么用多项式算CRC？

这是个重要的问题。
关于为什么用多项式算余数而不是直接用二进制数计算，一种解答是“多项式表示循环冗余校验过程比较方便”，我的理解是，

1. 用多项式可以直接根据x的power幂次判断1分别处在第几位；
2. 打个比方，现在要计算101 mod 11(modulo-2 division)，
   2.1 GF(2)上只有{0,1}这两个单位元，不存在101和11这两个元素，所以如果你要计算101模二除以11，实际上跟GF(2)没什么关系。而$x^2+1$和$x+1$这两个多项式可以在GF(2)上计算，因为x取{0,1}实际上用modulo-2 addition和modulo-2 multiplication结果还是在{0,1}里；
   2.2 为什么非要用模二除？模二除不需要退位，因此可以用XOR计算，相当高效。但实际上模二除跟正常除法的商和余数都是没关系的。A polynomial over GF(2) can be represented as a string of bits. An integer can be represented as a string of bits. There the similarity ends. They are two entirely different beasts. 这个通过下面那段（来自asecuritysite的）代码计算101和11的例子就一目了然了。

Binary form:	101  divided by  11
Decimal form:	5  divided by  3

x**2+1
x+1

Divide operation:

Result is	11
Remainder is	0
Working is	

 11 
--- 
101
11
--
 11
 11
 --
  0

import struct
import sys
val1='1010'
val2='110'

if (len(sys.argv)>1):
  val1=str(sys.argv[1])

if (len(sys.argv)>2):
  val2=str(sys.argv[2])


def showpoly(a):
  str1 = ""
  nobits = len(a)
  for x in range (0,nobits-2):
    if (a[x] == '1'):
      if (len(str1)==0):
        str1 +="x**"+str(nobits-x-1)	
      else: 
        str1 +="+x**"+str(nobits-x-1)
  if (a[nobits-2] == '1'):
    if (len(str1)==0):
      str1 +="x"
    else:
      str1 +="+x"

  if (a[nobits-1] == '1'):
    str1 +="+1"
  print(str1)
	

def toList(x):
  l = []
  for i in range (0,len(x)):
    l.append(int(x[i]))
  return (l)

def toString(x):
  str1 =""
  for i in range (0,len(x)):
    str1+=str(x[i])
  return (str1)

def divide(val1,val2):
  a = toList(val1)
  b = toList(val2)
  working=""
  res=""
  while len(b) <= len(a) and a:
    if (a[0] == 1):
      del a[0]
      for j in range(len(b)-1):
        a[j] ^= b[j+1]
      if (len(a)>0):
        working +=toString(a)
        res+= "1"
      else:
        del a[0]
        working +=toString(a)
        res+="0"
  print("Result is\t",res)
  print("Remainder is\t",toString(a))
  return 

print("Binary form:\t",val1," divided by ",val2)
print("Decimal form:\t",int(val1,2)," divided by ",int(val2,2))
print("")

showpoly(val1)
showpoly(val2)

print("\nDivide operation:\n")

divide(val1,val2)

所以用多项式计算CRC。
11不可以在GF(2)而x+1可以在GF(2)对吗？

Example

To compute an n-bit binary CRC, line the bits representing the input in a row, and position the (n + 1)-bit pattern representing the CRC’s divisor (called a “polynomial”) underneath the left end of the row.
In this example, we shall encode 14 bits of message with a 3-bit CRC, with a polynomial x^3 + x + 1. The polynomial is written in binary as the coefficients; a 3rd-degree polynomial has 4 coefficients (1x^3 + 0x^2 + 1x + 1). In this case, the coefficients are 1, 0, 1 and 1. The result of the calculation is 3 bits long, which is why it is called a 3-bit CRC. However, you need 4 bits to explicitly state the polynomial.

要计算n位CRC（CRC-n-XXX），把比特表示列在一行里，并把n+1位的CRC除数多项式放在下一行的最左侧。
在例子里，我们用3位CRC编码14位消息（11010011101100），用的是$x^3 + x + 1$。多项式系数用二进制表示，一个3阶多项式有4个系数$(1x^3 + 0x^2 + 1x + 1)$。在例子里系数分别是1, 0, 1, 1。计算的结果是3位长度的，但是需要4位来明确地表示多项式。

This is first padded with zeros corresponding to the bit length n of the CRC. This is done so that the resulting code word is in systematic form. Here is the first calculation for computing a 3-bit CRC:

所谓的模二除法其实跟上文的模二加法模二乘法一个意思，在长除的时候模二除法不需要借位（退位减），因此可以直接用XOR计算。

11010011101100 000 <--- input right padded by 3 bits
1011               <--- divisor (4 bits) = x³ + x + 1
------------------
01100011101100 000 <--- result

The algorithm acts on the bits directly above the divisor in each step. The result for that iteration is the bitwise XOR of the polynomial divisor with the bits above it. The bits not above the divisor are simply copied directly below for that step. The divisor is then shifted right to align with the highest remaining 1 bit in the input, and the process is repeated until the divisor reaches the right-hand end of the input row. Here is the entire calculation:

这种算法每一步都作用于除数正上方的位。迭代的结果是多项式除数与上面对应位的按位异或。不在除数上方的位直接复制到下方。然后将除数右移以与输入中剩余的最高 “1” 位对齐，并重复该过程，直到除数到达输入行的右端。 这是整个计算过程：

11010011101100 000 <--- input right padded by 3 bits
1011               <--- divisor
01100011101100 000 <--- result (note the first four bits are the XOR with the divisor beneath, the rest of the bits are unchanged)
 1011              <--- divisor ...
00111011101100 000
  1011
00010111101100 000
   1011
00000001101100 000 <--- note that the divisor moves over to align with the next 1 in the dividend (since quotient for that step was zero)
       1011             (in other words, it doesn't necessarily move one bit per iteration)
00000000110100 000
        1011
00000000011000 000
         1011
00000000001110 000
          1011
00000000000101 000
           101 1
-----------------
00000000000000 100 <--- remainder (3 bits).  Division algorithm stops here as dividend is equal to zero.

Since the leftmost divisor bit zeroed every input bit it touched, when this process ends the only bits in the input row that can be nonzero are the n bits at the right-hand end of the row. These n bits are the remainder of the division step, and will also be the value of the CRC function (unless the chosen CRC specification calls for some postprocessing).
The validity of a received message can easily be verified by performing the above calculation again, this time with the check value added instead of zeroes. The remainder should equal zero if there are no detectable errors.

因为最左边的除数位会让任何碰到的输入位变成0，当它处理结束时仅剩的1就是这行最右侧的n位CRC校验值了。这n位就是模二除的余数，也是CRC方程的值（除非选择的CRC需要做后处理），
收到的消息的有效性可以通过简单地重复上面的计算过程验证，这次附加的n位不是0，是之前计算的余数。如果没有可检测的错误，这次计算的余数应该等于0，像下面的演示一样。

11010011101100 100 <--- input with check value
1011               <--- divisor
01100011101100 100 <--- result
 1011              <--- divisor ...
00111011101100 100

......

00000000001110 100
          1011
00000000000101 100
           101 1
------------------
00000000000000 000 <--- remainder

RAID2, 3, 4, 5, 6

经过上面这一大堆啰嗦的前置知识，终于可以搞懂RAID2了——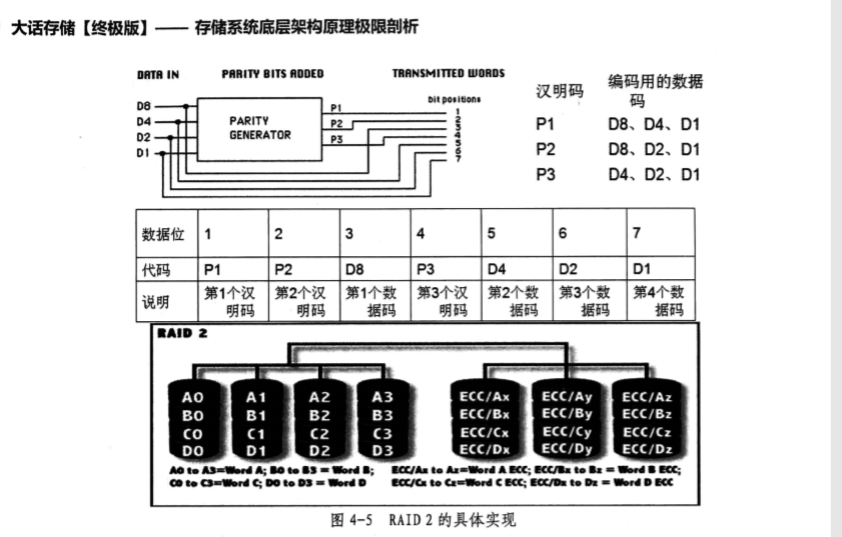




RAID3使用上面提到的奇偶校验代替了汉明码，所以只需要一个校验盘做错误校正和检测。
RAID4跟RAID3几乎相同，只是RAID4是按数据块而不是像RAID3一样按位访问。
RAID5和RAID-Z1类似，相比RAID3的单独一个校验盘，RAID5将校验位分散到了各个盘上。

RAID6和RAID-Z2类似，相比RAID5只是多了一位校验位，双重奇偶校验。

Reference

https://en.wikipedia.org
https://forums.freebsd.org
https://docs.freebsd.org/en/books/handbook/
https://docs.freebsd.org/zh-cn/books/handbook/
https://man.freebsd.org/cgi/man.cgi
https://docs.freebsd.org/en/books/arch-handbook/
https://book.bsdcn.org
Channel Codes