#include <iostream>
#include <string>
#include <vector>
#define VERTEX 13
using namespace std;
struct AdjacencyMatrix {
string vertex[VERTEX];
int edges[VERTEX][VERTEX];
int isTraversed[VERTEX] = { 0 };
vector<int> path;
vector<pair<vector<int>, int>> pathcost;
};
class Solution {
public:
void createGraph(AdjacencyMatrix &graph) {
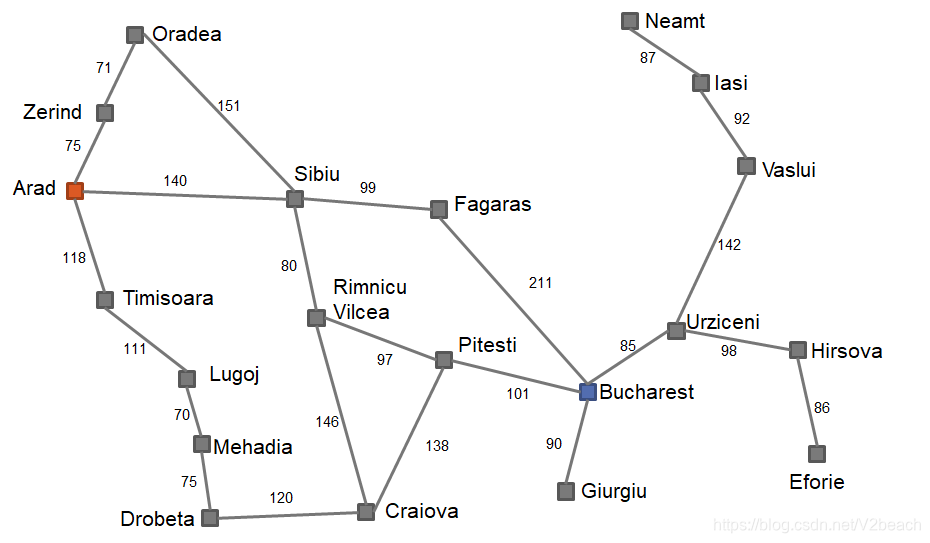
int map[VERTEX][VERTEX] = { { 0, 75, -1,118, -1, -1, -1,140, -1, -1, -1, -1, -1 },
{ -1, 0, 71, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1 },
{ -1, -1, 0, -1, -1, -1, -1,151, -1, -1, -1, -1, -1 },
{ -1, -1, -1, 0,111, -1, -1, -1, -1, -1, -1, -1, -1 },
{ -1, -1, -1, -1, 0, 70, -1, -1, -1, -1, -1, -1, -1 },
{ -1, -1, -1, -1, -1, 0, 75, -1, -1, -1, -1, -1, -1 },
{ -1, -1, -1, -1, -1, -1, 0, -1, -1,120, -1, -1, -1 },
{ -1, -1, -1, -1, -1, -1, -1, 0, 80, -1, 99, -1, -1 },
{ -1, -1, -1, -1, -1, -1, -1, -1, 0,146, -1, 97, -1 },
{ -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1,138, -1 },
{ -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1,211 },
{ -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0,101 },
{ -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0 }
};
for (int i = 0; i < VERTEX; i++)
for (int j = 0; j < VERTEX; j++)
if (map[i][j] != -1)
map[j][i] = map[i][j];
memcpy(graph.edges, map, sizeof(map));
graph.vertex[0] = "Arad";
graph.vertex[1] = "Zerind";
graph.vertex[2] = "Oradea";
graph.vertex[3] = "Timisoara";
graph.vertex[4] = "Lugoj";
graph.vertex[5] = "Mehadia";
graph.vertex[6] = "Drobeta";
graph.vertex[7] = "Sibiu";
graph.vertex[8] = "Rimnicu-Vilcea";
graph.vertex[9] = "Craiova";
graph.vertex[10] = "Fagaras";
graph.vertex[11] = "Pitesti";
graph.vertex[12] = "Bucharest";
}
void outputGraph(AdjacencyMatrix &graph) {
for (int i = 0; i < VERTEX; i++)
for (int j = 0; j < VERTEX; j++)
if (graph.edges[i][j] > 0)
cout << graph.vertex[i] << " -> " << graph.vertex[j] << " : " << graph.edges[i][j] << endl;
}
int nextOutdegree(AdjacencyMatrix graph, int interrupt, int loc) {
for (int index = interrupt + 1; index < VERTEX; index++) {
if (graph.edges[loc][index] > 0 && graph.isTraversed[index] == 0)
return index;
}
return -1;
}
int computePathCost(AdjacencyMatrix graph) {
int cost = 0, index = 0;
for (; index < graph.path.size() - 1; index++)
cost += graph.edges[graph.path[index]][graph.path[index + 1]];
cost += graph.edges[graph.path[index]][12];
return cost;
}
int minimumPathCost(vector<pair<vector<int>, int>> pathcost) {
int minIndex = 0, index = 1;
for (; index < pathcost.size(); index++)
if (pathcost[minIndex].second >= pathcost[index].second)
minIndex = index;
return minIndex;
}
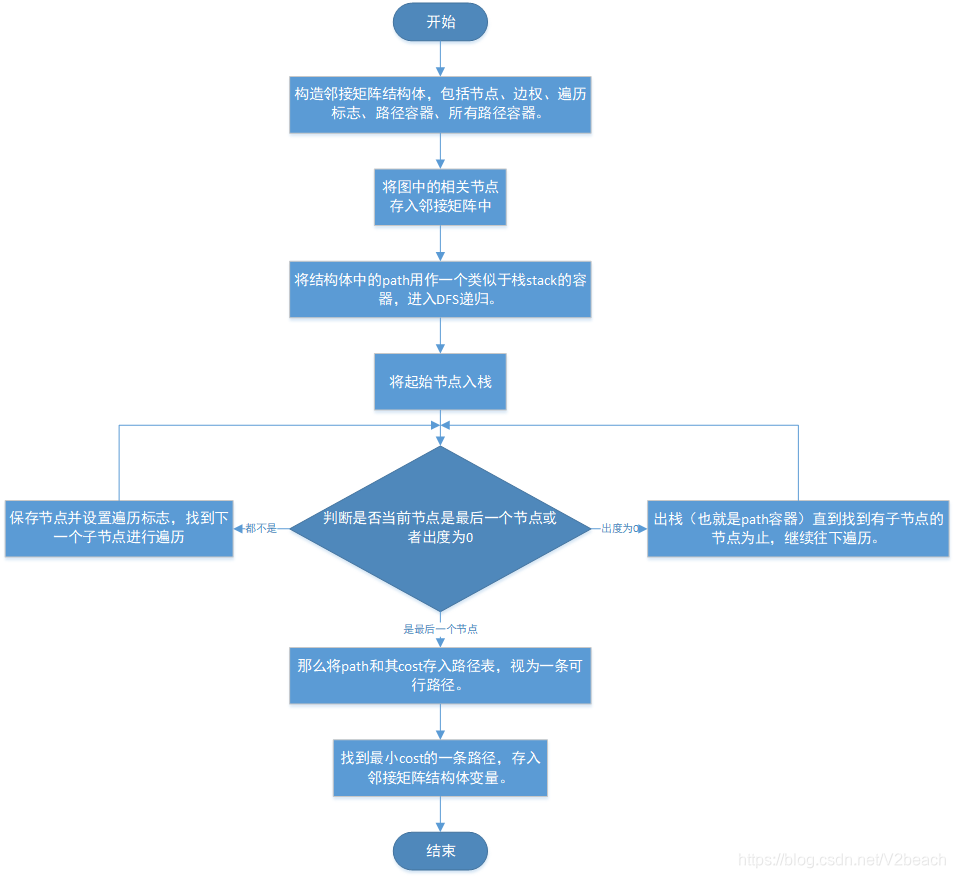
void depthFirstSearch(AdjacencyMatrix &graph, int start, int end) {
int loc = 0, cost = 0;
graph.isTraversed[start] = 1;
graph.path.push_back(start);
while ((loc = nextOutdegree(graph, loc, start)) != -1) {
if (loc == end) {
cout << "Path: ";
for (int cur = 0; cur < graph.path.size(); cur++) {
cout << graph.vertex[graph.path[cur]] << " ";
cost = computePathCost(graph);
graph.pathcost.push_back(pair<vector<int>, int>(graph.path, cost));
}
cout << graph.vertex[end] << ", Cost: " << cost << endl;
break;
}
depthFirstSearch(graph, loc, end);
graph.path.pop_back();
graph.isTraversed[loc] = 0;
}
}
};
int main(int argc, char *argv[]) {
int start = 0, end = 12, index = 0;
AdjacencyMatrix graph;
Solution sol;
sol.createGraph(graph);
sol.outputGraph(graph);
sol.depthFirstSearch(graph, start, end);
index = sol.minimumPathCost(graph.pathcost);
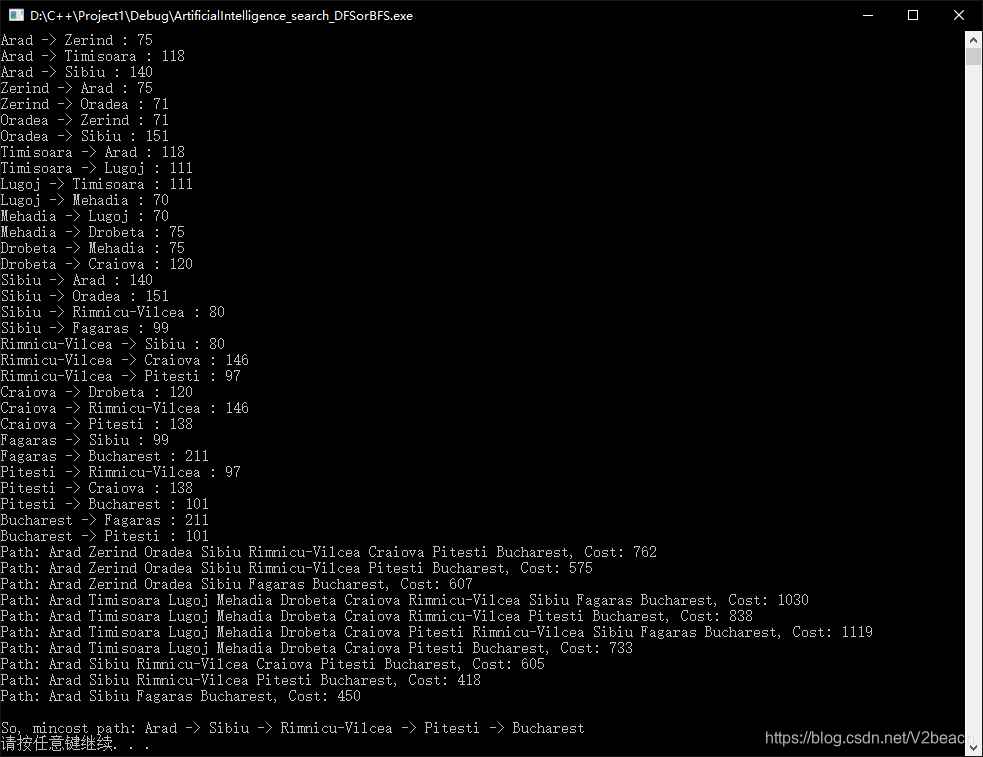
cout << endl << "So, mincost path: ";
for (int cur = 0; cur < graph.pathcost[index].first.size(); cur++)
cout << graph.vertex[graph.pathcost[index].first[cur]] << " -> ";
cout << graph.vertex[end] << endl;
vector<int>().swap(graph.path);
system("pause");
return 0;
}
|