二项分布 (Binomial Distribution)

Part Ⅰ

X~B(n,p)

分布律：$P(X=k) = {n\choose k}p^kq^{n-k}，k = 0,1,2,..,n，q = 1-p$
期望：
$$
EX = \sum_{k=0}^n k {n\choose k}p^kq^{n-k} \
= \sum_{k=1}^n k {n\choose k}p^kq^{n-k} \
= \sum_{k=1}^n k {\frac{n!}{k!(n-k)!}}p^kq^{n-k} \
= np\sum_{k=1}^n {\frac{(n-1)!}{(k-1)!(n-k)!}}p^{k-1}q^{(n-1)-(k-1)} \
= np\sum_{k=1}^n{n-1\choose k-1}p^{k-1}q^{(n-1)-(k-1)}\
= np[{n-1\choose 0}p^0q^{n-1}+{n-1\choose 1}p^1q^{n-2}+…+{n-1\choose n-1}p^{n-1}q^0] \
= np
$$
方差：$DX = EX^2-(EX)^2$
计算EX^2：
$$
EX^2 = \sum_{k=1}^nk^2{n\choose k}p^kq^{n-k}, k = 0,1,2,..,n,q = 1-p\
= \sum_{k=1}^n[k(k-1)+k]{n\choose k}p^kq^{n-k}\
= \sum_{k=1}^nk(k-1){n\choose k}p^kq^{n-k} + \sum_{k=1}^nk{n\choose k}p^kq^{n-k}\
其中，
\sum_{k=1}^nk{n\choose k}p^kq^{n-k} = EX = np\
\sum_{k=1}^nk(k-1){n\choose k}p^kq^{n-k} \
= \sum_{k=1}^nk(k-1){\frac{n!}{k!(n-k)!}}p^2p^{k-2}q^{n-k} \
= \sum_{k=2}^nk(k-1){\frac{n!}{k!(n-k)!}}p^2p^{k-2}q^{n-k} \
$$注：特别注意这里k=1时项为0，所以可以从k=2开始计算。$$\
= \sum_{k=1}^n{\frac{n(n-1)(n-2)!}{(k-2)!(n-k)!}}p^2p^{k-2}q^{[(n-2)-(k-2)]} \
= n(n-1)p^2\sum_{k=2}^n{\frac{(n-2)!}{(k-2)!(n-k)!}}p^{k-2}q^{[(n-2)-(k-2)]}\
= n(n-1)p^2\sum_{k=2}^n{n-2\choose k-2}p^{k-2}q^{[(n-2)-(k-2)]}\
= n(n-1)p^2 \
\rightarrow EX^2 = n(n-1)p^2+np \ $$$$
\rightarrow DX = EX^2-(EX)^2 = np-np^2 = np(1-p)
$$

Part Ⅱ 0-1分布

X~B(1,p)

也可以从上式直接推导得到

泊松分布 (Poisson’s Distribution)

X~P($\lambda$)

分布律：$P(X=k)=\frac{\lambda ^{k}e^{-\lambda }}{k!}$
期望：
$$
E(X)=\sum_{k=0}^{\infty }k\cdot \frac{\lambda ^{k}e^{-\lambda }}{k!} \ $$$$
因为k=0时，
k⋅λke−λk!=0 \ $$$$
E(X)=\sum_{k=1}^{\infty }k\cdot \frac{\lambda ^{k}e^{-\lambda }}{k!} \ $$$$
E(X)=\sum_{k=1}^{\infty }k\cdot \frac{\lambda ^{k}e^{-\lambda }}{k!}=\sum_{k=1}^{\infty } \frac{\lambda ^{k}e^{-\lambda }}{(k-1)!}=\sum_{k=1}^{\infty } \frac{\lambda ^{k-1}\lambda e^{-\lambda }}{(k-1)!}=\lambda e^{-\lambda }\sum_{k=1}^{\infty } \frac{\lambda ^{k-1}}{(k-1)!} \ $$$$
用到泰勒展开式：e^{x}=1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+…+\frac{x^{n}}{n!}+…=\sum_{k=1}^{\infty } \frac{x ^{k-1}}{(k-1)!} \ $$$$
E(X)=\lambda e^{-\lambda }\sum_{k=1}^{\infty } \frac{\lambda ^{k-1}}{(k-1)!}=\lambda e^{-\lambda }e^{\lambda }=\lambda
$$
方差：$DX = EX^2-(EX)^2$
计算EX^2：
$$
E(X^2)=\sum_{k=0}^{\infty }k^2 \cdot \frac{\lambda ^{k}e^{-\lambda }}{k!}=\lambda e^{-\lambda} \sum_{k=1}^{\infty } \frac{k \lambda ^{k-1}}{(k-1)!}=\lambda e^{-\lambda} \sum_{k=1}^{\infty } \frac{(k-1+1) \lambda ^{k-1}}{(k-1)!} \ $$$$
=\lambda e^{-\lambda} (\sum_{m=0}^{\infty } \frac{m \cdot \lambda ^{m}}{m!}+\sum_{m=0}^{\infty } \frac{ \lambda ^{m}}{m!}) (m=k-1) \ $$$$
=\lambda e^{-\lambda} ( \lambda \cdot \sum_{m=1}^{\infty } \frac{\lambda ^{m-1}}{(m-1)!}+\sum_{m=0}^{\infty } \frac{ \lambda ^{m}}{m!}) \ $$$$
=\lambda e^{-\lambda}(\lambda e^{\lambda}+e^\lambda)=\lambda(\lambda+1) \ $$$$
\rightarrow D(X)=E(X^2)-(E(X))^2=\lambda(\lambda+1)-\lambda^2=\lambda
$$

均匀分布 (Uniform Distribution)

X~U(a,b)

推导较为简单。

正态分布 (Normal Distribution)

X~N(μ,σ)

概率密度函数：$f_X(x) =\frac{1}{\sigma\sqrt{2\pi}}\exp\left{-\frac{(x-\mu)^2}{2\sigma^2}\right}$


期望：$E(x) = \mu\int_{-\infty}^{+\infty}\mathcal{N}(x|\mu’ = 0, \sigma^2)dx = \mu$

方差：$\Rightarrow V(X) = \sigma^2\frac{4}{\sqrt{\pi}}\frac 12 \frac {\sqrt \pi}{2} = \sigma^2$

指数分布 (Exponential Distribution)https://blog.csdn.net/saltriver/article/details/53982885)

X~Γ(1,β)

概率密度函数：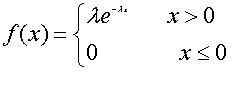
期望：
$$
E(X)=\int_{-\infty }^{\infty }|x|f(x)dx=\int_{0}^{\infty }xf(x)dx=\int_{0}^{\infty }x\cdot\lambda e^{-\lambda x}dx=\frac {1} {\lambda}\int_{0}^{\infty }\lambda xe^{-\lambda x}d\lambda x \
令u=λx，E(X)=\frac {1} {\lambda}\int_{0}^{\infty }ue^{-u}du=\frac {1} {\lambda}[(-e^{-u}-ue^{-u})|(\infty,0)]=\frac {1} {\lambda} \
$$
方差：$DX = EX^2-(EX)^2$
计算EX^2：
$$
E(X^2)=\int_{-\infty }^{\infty }|x^2|f(x)dx=\int_{0}^{\infty }x^2f(x)dx=\int_{0}^{\infty }x^2\cdot\lambda e^{-\lambda x}dx \
E(X^2)=\frac {1} {\lambda^2}\int_{0}^{\infty }\lambda x \lambda xe^{-\lambda x}d\lambda x \
令u=λx，E(X^2)=\frac {1} {\lambda^2}\int_{0}^{\infty }u^2e^{-u}du=\frac {1} {\lambda^2}[(-2e^{-u}-2ue^{-u}-u^2e^{-u})|(\infty,0)]=\frac {1} {\lambda^2}\cdot 2=\frac {2} {\lambda^2} \
\rightarrow D(X)=E(X^2)-(E(X))^2=\frac {2} {\lambda^2}-(\frac {1} {\lambda})^2=\frac {1} {\lambda^2}
$$