SSL certificate

2025-03-09 22:02:09 42 分钟读完 (大约 6320 个字)

Categories:

technology

Tags: Certificate, Encryption, Hash

Secure Sockets Layer（安全套接字层）技术上已经被弃用，只是习惯上仍如此称呼，现在用的技术是更高效有效的Transport Layer Security（TLS，传输层安全）。本文除了分析协议全过程外还涉及证书申请和证书内容、加密算法和哈希算法。

协议总览

[客户端] ------> [服务器]
   Client Hello  ------>  Server Hello + 证书
   验证证书
   生成 Pre-Master Secret
   使用公钥加密  ------>  私钥解密 + 会话密钥生成
   [加密数据传输]

握手阶段

SSL/TLS Handshake

1. 客户端Hello

client向server发送一个Hello消息，包括：

支持的SSL/TLS版本
支持的加密算法（AES，chacha？，RSA，DES？等 gcm呢？
随机数client random用于生成密钥
其他扩展信息如SNI（Server Name Indication，服务器名称指示），如果一个ip上有多个服务可以用SNI指定域名

2. 服务器Hello

server向client回复一个Hello消息，包括：

确认使用的SSL/TLS版本
确认的加密算法
随机数server random用于生成密钥
服务器的SSL/TLS证书（certificate）

3. 客户端对服务器的证书验证

Certificate Verification :

检查证书是否由受客户端信任的CA签发
检查证书是否已过期
检查证书的域名与目标服务器是否匹配

所以证书实际上只有在一台设备第一次访问服务器时会用到，验证过公钥可靠性之后，客户端保存下来公钥，只要公钥没被server改变也没被client删掉，证书就不再参与加密过程了。

证书内容

.pem, .crt文件里的-----BEGIN CERTIFICATE-----, ..., -----END CERTIFICATE-----看起来是乱码通常是 Base64 编码的 ASN.1（二进制）数据，二进制易于存储传输。
根据 X.509 标准，用openssl x509 -in example.crt -text -noout命令解码后证书中包含以下信息：

版本号（Version）：证书使用的 X.509 版本（如 v3）。
序列号（Serial Number）：证书的唯一标识号。
签名算法（Signature Algorithm）：用于签名的算法（如 RSA）。
颁发机构（Issuer）：签发证书的 CA（证书颁发机构）。
有效期（Validity）：证书的起始日期和过期日期。
主体（Subject）：证书所属实体（如网站域名）。
公钥信息（Public Key）：包含公钥及其算法。
扩展字段（Extensions）：包括用途等。
签名（Signature）：由 CA 用其私钥生成，用于验证证书的真实性。

按适用范围分类有三种：

单域名证书：保护单个域名，如 example.com，不适用于 sub.example.com；
多域名证书（SAN 证书，Subject Alternative Name）：允许多个不同域名共享一个证书，如 a.com、b.net、c.org；
泛域名证书（Wildcard Certificate）：适用于主域名及所有子域名，例如 *.example.com 可用于：www.example.com、mail.example.com、blog.example.com，但不支持二级以上子域名（如 a.b.example.com）。

ACME协议

ACME协议的工具有：

Certbot（Let’s Encrypt 官方推荐）
acme.sh（轻量级 Shell 脚本实现）
LEGO（Go 语言实现）

Let’s Encrypt的官网是不能申请证书的，完全通过 ACME client 操作，官方提供的是 certbot。

ACME（Automatic Certificate Management Environment，自动证书管理环境）是一种用于自动化管理TLS/SSL证书的协议，由Let’s Encrypt和Internet Security Research Group (ISRG) 开发并由 IETF（Internet Engineering Task Force）标准化，定义在 RFC 8555。

这里选用 acme.sh ，因为我希望尽量轻量而且一步到位完全自动，想要在我阿里云 CDN + OSS 的架构上自动申请证书要先回忆一下我到底是怎么搭建博客的。

首先hexo生成的是静态网站，这个static不是说没有Javascript的动态交互，而是说没有数据库操作，服务端只提供html等资料，部署在OSS（Object Storage Service）就跟存在网盘或者图床上的资源差不多性质。
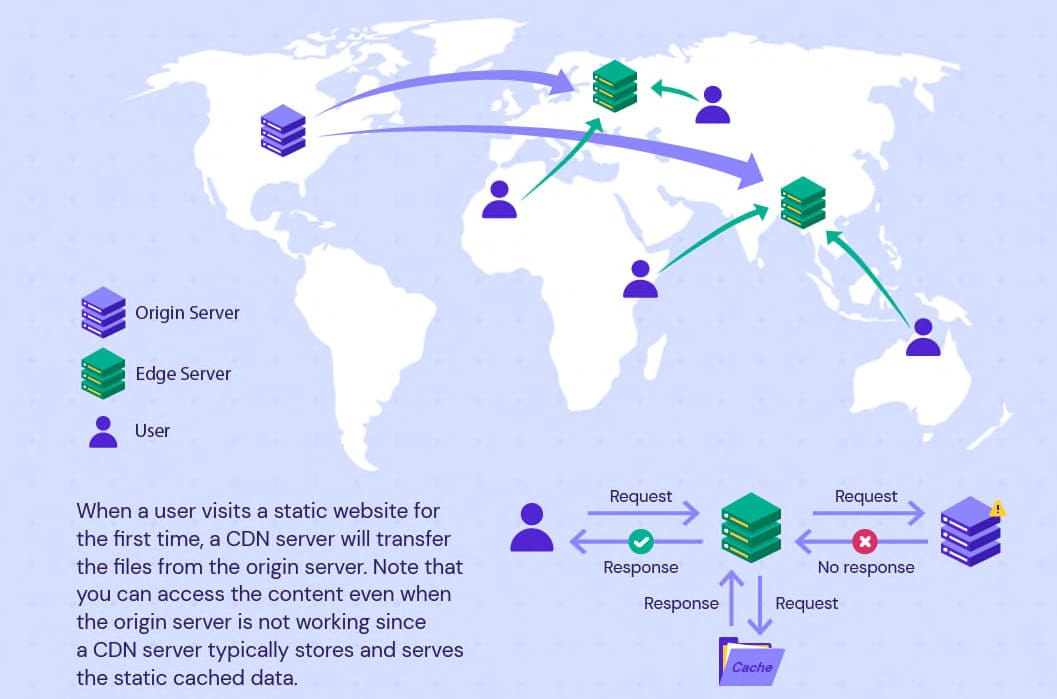
然后我用CDN（Content delivery network）提升访问速度，以本网站的 wiki 为例，
- 阿里云 CDN 服务的 Edge Servers 域名是 wiki.v2beach.cn.w.kunlunaq.com，wiki 本身通过阿里云 DNS 的 CNAME（域名→域名）映射到这个域名，这个域名再映射到下图所示的多个边缘服务器。
- 如果 CDN 上没有缓存，会进行回源访问 v2beach.github.io:443 这个 GitHub Pages 源站，如果是 blog.v2beach.cn 的 CDN blog.v2beach.cn.w.kunlunca.com 上缓存不命中则是回源到 blog-v2beach-cn.oss-cn-chengdu.aliyuncs.com:443 这个 oss 原址上，试图将静态资源缓存到 CDN。

所以实际上我需要的是将申请到的证书再上传到阿里云证书管理服务，并部署到 CDN 上。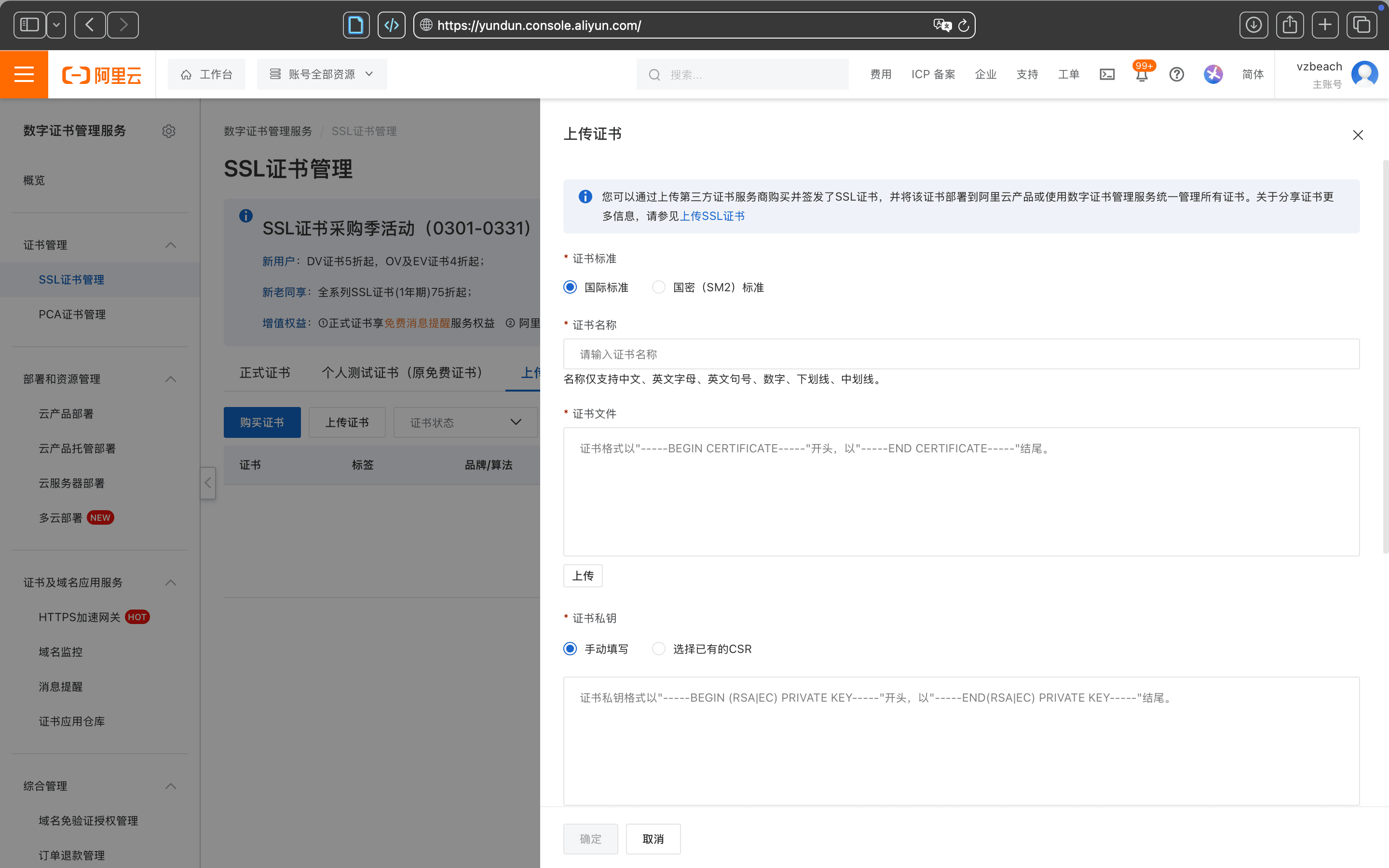

好在七八年前的这个 issue 里有人已经写过了 deploy/ali_cdn：
安装阶段 acme.sh 做了这些操作：

Create and copy acme.sh to your home dir ($HOME): ~/.acme.sh/. All certs will be placed in this folder too.
Create alias for: acme.sh=~/.acme.sh/acme.sh.
Create daily cron job to check and renew the certs if needed.
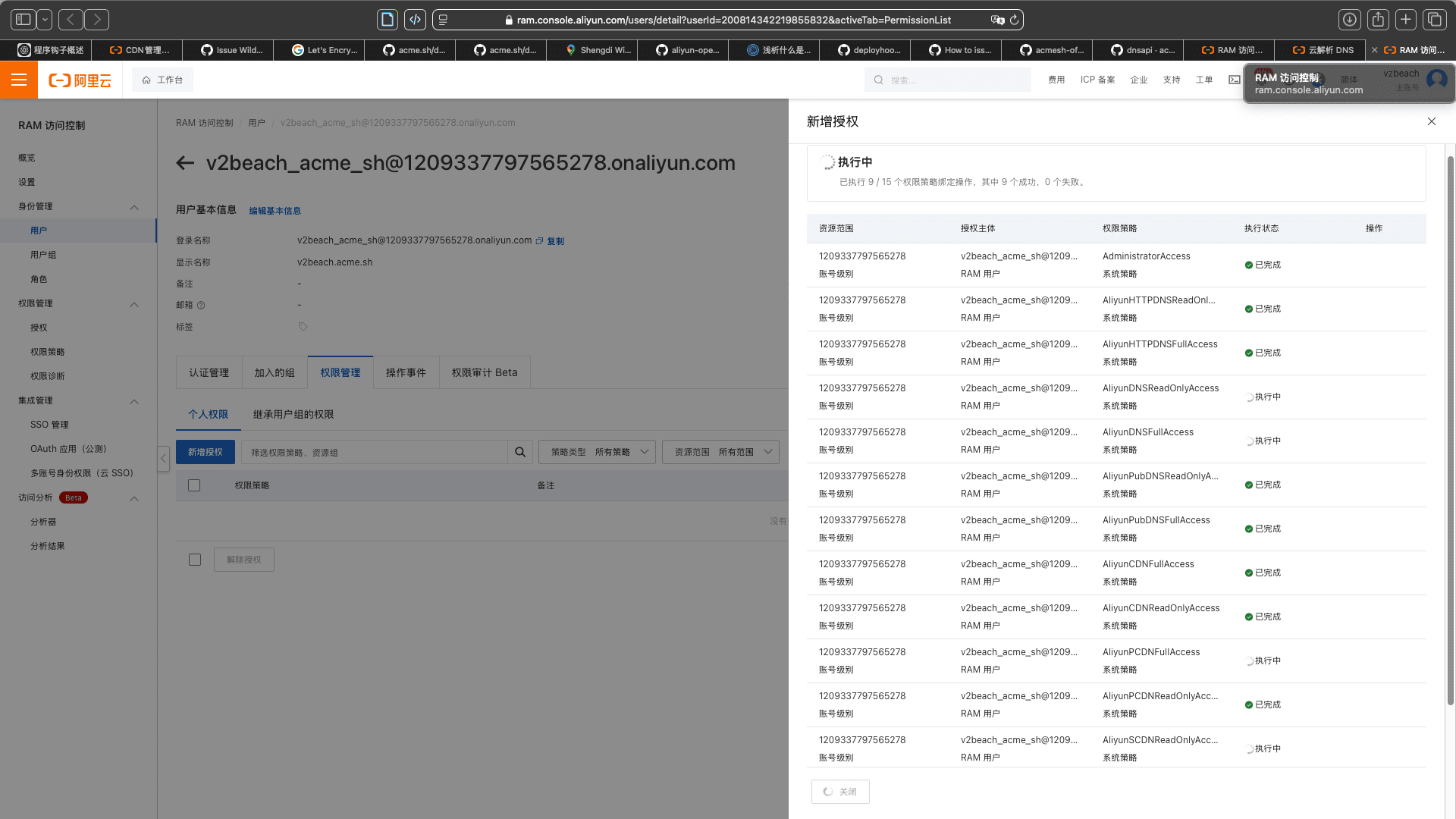
然后就可以 issue certs（签发证书）了，根据 How to issue a cert 和在阿里云 DNS 添加 txt 记录从而自动签发的 api

这两步阿里云 api 要申请权限。

./acme.sh --issue --dns dns_ali -d 'v2beach.cn' -d '*.v2beach.cn'

为主域名和子域名一块申请泛域名证书。
之后在阿里云 CDN 部署证书，根据 deplothooks 文档，

export DEPLOY_ALI_CDN_DOMAIN="blog.v2beach.cn wiki.v2beach.cn"
./acme.sh --deploy -d 'v2beach.cn' --deploy-hook ali_cdn

这里部署的域名是被加速的域名，而不是 Edge Servers CNAME 域名。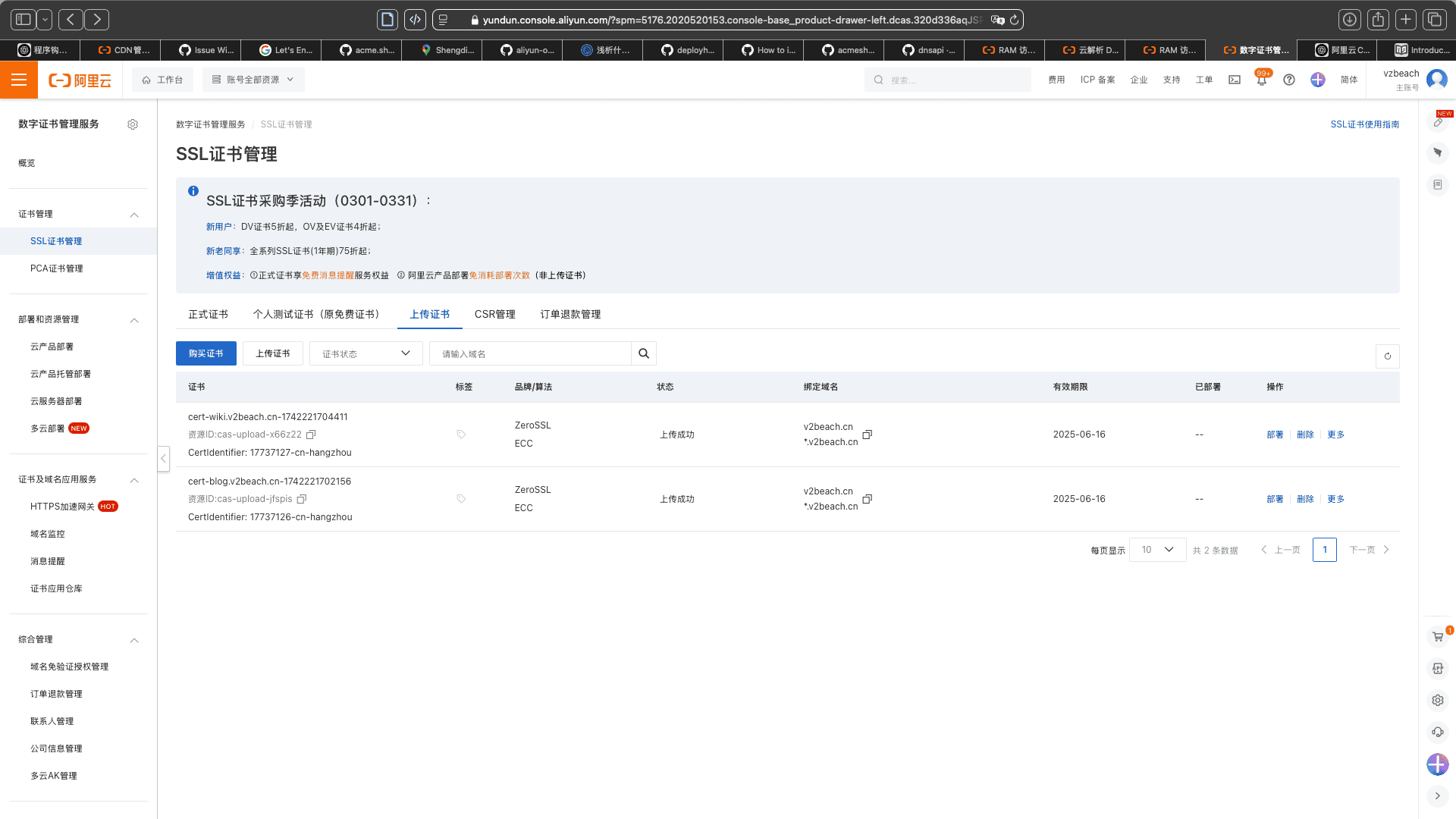
完成，希望自动配置的 cron 任务顺利更新

原来 cron 定时任务这个单词跟 chrono ark 是同一个词源，都是来自希腊语的时间。

本来想用 Docker 管理，但离开商汤后两年没用了，手生没办法还是用 git 操作了。

Let’s Encrypt证书内容

证书签发过程中除了上面证书内容里说的.pem, .crt之外还会有.key文件（即私钥），公钥已经包含在证书文件里了。
这个密钥是在 server hello 里跟 client 传证书时数字签名用的。

[Mon Mar 17 22:14:34 CST 2025] Your cert is in: /Users/v2beach/.acme.sh/v2beach.cn_ecc/v2beach.cn.cer
[Mon Mar 17 22:14:34 CST 2025] Your cert key is in: /Users/v2beach/.acme.sh/v2beach.cn_ecc/v2beach.cn.key
[Mon Mar 17 22:14:34 CST 2025] The intermediate CA cert is in: /Users/v2beach/.acme.sh/v2beach.cn_ecc/ca.cer
[Mon Mar 17 22:14:35 CST 2025] And the full-chain cert is in: /Users/v2beach/.acme.sh/v2beach.cn_ecc/fullchain.cer

每个证书都包含证书链，证书链里每一个证书（Root CA，Intermediate CA）都要被验证通过，否则证书验证失败。

[服务器证书]  <-- 由 [中间 CA] 签发
[中间 CA]  <-- 由 [根 CA] 签发
[根 CA]  <-- 由 操作系统/浏览器 预置信任

根 CA 采用分层架构是为了极大降低根 CA 私钥使用频率，中间 CA 被攻破的情况下会受中间人攻击的服务器大大减少。

根 CA 只用于签发中间 CA 证书，签发频率极低（可能几年才用一次）。
根 CA 私钥存储在离线环境（HSM 设备），并且通常处于冷存储，无法通过网络访问，极大降低了攻击面。即使根 CA 被攻破，攻击者仍然需要物理访问HSM 设备（Hardware Security Module，硬件安全模块是一种专门用于存储和保护加密密钥的硬件设备），否则无法使用私钥进行签发。
相比之下，如果根 CA 直接签发每一个终端证书，私钥必须频繁使用，暴露在在线环境的风险更大。

openssl x509 -in /Users/v2beach/.acme.sh/v2beach.cn_ecc/v2beach.cn.cer -noout -text 翻译二进制证书，基本符合上面证书内容部分列举的内容。

4. 生成各种密钥

随机生成预主密钥 (Pre-Master Secret)；
用Pre-Master Secret和client random以及server random共同生成主密钥 (Master Secret)；
用Master Secret派生出一系列会话密钥 (Session Key)。

生成Session Key本身的过程用非对称加密传输随机数密钥，这个Session Key进而用于数据传输的对称加密。

为什么费劲两轮加密？第一次非对称加密是想办法在不直接传输密钥的情况下让客户端和服务器得到相同密钥，因为如果直接传输约定的密钥，只需截获这个信息和加密算法（通过任何渠道——截获Hello，穷举，从密钥反推都可以得到加密算法），第三方破译信息甚至伪装成客户端或服务器也就轻而易举了。之后的对称加密则是在确保密钥不泄漏的情况下进行安全的数据传输了。

如果用RSA传输Pre-Master Secret

Client: [客户端随机生成 48 Bytes Pre-Master Secret] → [使用服务器公钥（Server Hello中获得）加密] → [发送给服务器]
Server: [用私钥解密] → [获得 Pre-Master Secret]

很自然地提问，为什么SSL/TLS中不角色互换，让服务端随机生成PMS，而客户端保存私钥提供公钥？

客户端私钥容易丢失；
RSA私钥解密计算开销大（$c^d \mod n$），pc或许可以承受，移动端就加重设备负担；
chatgpt说会加大MITM风险（Man-In-The-Middle，中间人攻击）？可是中间人攻击应该是从server Hello就拦截掉了，向client伪造自己是server。向server伪造自己是client，按我的理解MITM攻击跟谁存私钥关系不大。

算法细节总结在下文Rivest–Shamir–Adleman。

举例来说，假如p=2，q=3，公钥指数e=5，计算只需要这三个数字。

$n = 2 \times 3=6$ ；
$\varphi(6) = (2 - 1) \times (3 - 1)=2$ ，跟6互质的有1和5；
选择互质的e=5， $\gcd(5, \varphi(6)) = 1$ ；
寻找这样一个d， $5 \times d \equiv 1 \mod 2$ ，这个私钥指数可以是…, -1, 1, 3, 5, 7, …，任何一个都可以解密，但一般选最小正整数这里即1，减少运算量；
公钥即（6, 5），私钥即（6, 1）。

假设要加密的明文M=3（M一般要设定0到n之间，否则会解密出错，所以p和q一般设置很大），加密过程：$C=3^5 \mod 6=3$；解密过程：$M=3^1 \mod 6=3$。
发现n过小的时候C=M，所以n甚至会设置为2048位的大数。
经验1. $0<M<n$ ；2. $n>10^{1024}$ 。

涉及参数分别是$p, q，n，\phi(n)，e\rightarrow d$，其中，n是要公开（不加密，明文）发送给客户端的，e是选定的跟n组成公钥一起公开，最后密文C是公开的，其他所有数字都是保密的。

如果用ECDH生成Pre-Master Secret

双方各自生成一个私钥（私密）和一个公钥（可公开）。
双方交换各自的公钥，用对方的公钥和自己的私钥，分别用椭圆曲线和一个基点（不是焦点，是曲线上的点）计算出相同的 Pre-Master Secret。

Client: [生成私钥 a] → [计算公钥 A = g^a mod p] → [发送 A]
Server: [生成私钥 b] → [计算公钥 B = g^b mod p] → [发送 B]
双方计算：Pre-Master Secret = B^a mod p = A^b mod p

PRF生成Master Secret

基于一段数字PMS生成另一段随机数字MS，但要求得知seed（Key）的情况下就能得到生成数字MS。

PRF (Pseudo-Random Function，伪随机函数) 在 TLS1.2 和 SSL 里用的是 MAC 和 HMAC，在 TLS1.3 里用的是安全优化后的 HKDF（HMAC-based Key Derivation Function）。

以HMAC(Hash-based Message Authentication Code)为例：

$\text{HMAC}(Key, Message) = Hash((Key \oplus \text{opad}) \parallel Hash((Key \oplus \text{ipad}) \parallel Message))$

$ \oplus $ ：按位异或 (XOR) 运算
$ \parallel $ ：表示字符串连接 (Concatenation)
pad ：填充常量（值为 0x…，与哈希块大小相同）

PRF(Secret, Label, Seed)=P_hash(Secret, Label + Seed)

Secret：Pre-Master Secret 或 Master Secret
Label：一个ASCII字符串标签，表示当前正在生成的密钥类型（如 “master secret”、”key expansion” 等）
Seed：由客户端和服务器在 TLS 握手时交换的两个随机数 (ClientHello.random + ServerHello.random)
P_hash()：基于 HMAC 的递归扩展函数

总之就是按某种神秘复杂固定算法，能得到一个一一对应的map，即（Message，Key）对应哈希得到的唯一值。关于哈希算法之前一直没有细想过，为了不影响整体观感我在下文整理一些Hash算法。

PRF生成Session Key

用上述算法生成连接过程中SSL/TLS所需其他加密密钥。

5. 握手结束

双方使用会话密钥对“握手完成（Handshake Finished）”消息加密并发送，以确认握手成功。
根据RFC2246：

finished_label
           For Finished messages sent by the client, the string "client
           finished". For Finished messages sent by the server, the
           string "server finished".

之后与握手结束过程相同继续进行对称加密的数据交换。

加密算法

本质

将转为数字（比如直接转成定长的ASCII码拼起来）的信息，结合另一段数字（密钥），用具备某种数学性质的算法转换成一段乱码。
对于对称加密（Symmetric Encryption）来说相对简单，只需要一个互逆的数学变换$f$，满足：
- 其中K是密钥key，P是明文plaintext，C是密文ciphertext。比如最简单的例子，加减（$f=+, f^{-1}=-$）乘除（$f=\times , f^{-1}=\div $），或者异或XOR（$f=f^{-1}=\oplus $，因为$A\oplus A=0, A\oplus 0=A$）。
非对称加密（Asymmetric Encryption）则需要一个“单向陷门函数（One-way Trapdoor Function）”，说人话就是正向好计算，逆向如果没有密码就非常难算：
- 单向函数是已知x和f很容易计算f(x)，但已知f和f(x)很难反推出x。
- 陷门函数是用一个数学后门Key，能很容易用f和f(x, key)反推出x。
- f 就是易计算但难逆的数学函数（如大整数分解、椭圆曲线问题）。

比如在RSA中的单向陷门函数是$f(x) = x^e \mod n$，陷门trapdoor就是用通过欧拉函数得到的解密指数（私钥指数）d 求解$g(x)=y^d \mod n$。注意，对称算法是可逆函数$f, f^{-1}$，非对称算法不是f的可逆函数而是另一个相关函数g。

非对称

以SSL/TLS为例（服务端存私钥）的应用：

加密数据，client用server的公钥a加密b得到c并传输，server用私钥d解密c得到信息b；
- 加密任何单向数据，SSL/TLS里client加密发送Pre Master Secret用于生成后续密钥。
数字签名，server用私钥d加密b得到c并传输，client用server的公钥a解密c得到信息b，一方面能验证身份真实性（因为公钥a能解开就证明是公钥a对应server发送的信息），另一方面数字签名都会附加用SHA-256等哈希函数把信息b映射成e，用于客户端用同样的SHA-256映射信息b为f，通过e==f验证数据完整性。
- SSL/TLS里“服务器Hello”内包含的证书就需要数字签名，一开始的server Hello是没加密的，通过验证身份能避免伪造server。
- 邮件需要数字签名验证发件人身份和邮件内容完整，但是邮件是隐私，需要额外加密邮件内容。
- 软件需要数字签名验证制作者身份和软件内容完整，软件是公开内容一般不需要加密安装包等。

RSA的可逆性让它可被用做上述两种用途，client用server的公钥加密传输预主密钥，server用私钥数字签名证书传给client，只用一套公钥私钥，即key1加密key2可以解密，key2加密key1也可以解密。

那么一定存在其他加密算法只能key1加密key2解密，反之不行。

比如ElGamal分别有加密和数字签名两种用法，一样是在SSL/TLS中server存私钥这个例子，但一套密钥只能用于加密传输或数字签名一种用途，若用于加密传输就是client用server的公钥加密server收到后解密，若用于数字签名就是server用私钥加密client收到证书后解密验证。公钥若用来加密就不能反过来用同对私钥加密。

因为算法不可逆，反过来用密钥key2加密会导致key1无法解密（得用个key3解密）。

Rivest–Shamir–Adleman

这里R、S、A分别代表创造算法的三个人。

数学原理：

选择两个大素数 $p$ 和 $q$，计算它们的乘积： $n = p \times q$ ；
计算 $n$ 的欧拉函数（在数论中，对正整数n，欧拉函数φ(n)是小于或等于n的正整数中与n互质的数的数目。例如φ(8) = 4，因为1,3,5,7均和8互质。）： $\varphi(n) = (p - 1) \times (q - 1)$ ；
选择一个公钥指数 $e$，通常选择一个小的整数，使得 $e$ 与 $\varphi(n)$ 互质： $\gcd(e, \varphi(n)) = 1$ ；
计算私钥指数 $d$，满足： $e \times d \equiv 1 \mod \varphi(n)$ ，即求解： $d≡e^{−1} mod φ(N)$ ；
这样就得到公钥：$(n, e)$ 和私钥：$(n, d)$。

加密过程：$encrypted = message^e mod n$；
解密过程：$message = encrypted^d mod n$。

对称

AES

Advanced Encryption Standard，高级加密标准是一种分组加密算法，工作方式如下：

输入：固定长度的明文分组（128 位，即 16 字节）和密钥（128、192 或 256 位）。
加密过程：
经过多轮字节替换（SubBytes）、行移位（ShiftRows）、列混合（MixColumns）和轮密钥加（AddRoundKey）操作。
轮数取决于密钥长度：
AES-128：10 轮
AES-192：12 轮
AES-256：14 轮
其中，MixColumns 在最后一轮中被省略。
输出：加密后的密文（同样是 128 位）。

justmysocks-ss的gcm（Galois/Counter Mode）只是AES增加功能的特殊模式。

ChaCha20

ChaCha20 是一种流加密算法，基于Hash函数（MD5，SHA）和异或操作，不同于 AES 的分组加密。

输入：
256 位密钥（32 字节）
96 位随机数（Nonce）（12 字节）
计数器（32 位，避免重复）
加密过程：
以 512 位（64 字节）为单位生成伪随机密钥流。
明文和密钥流按位异或（XOR）。
通过 20 轮四分之一轮函数（Quarter Round）变换密钥流，确保扩散性。
输出：和明文长度相同的密文。

Hash

Hash 之所以叫 Hash 就是打碎、混合原本信息，转为定长值，用于超快的 O(1) 数组索引读操作，或达到保证数据完整安全的效果。

SHA-1/SHA-256, MD5 都是注重安全性的哈希算法，不只要求Key和Value一一对应，而且要求算法不可逆，即已知算法本身和Value，非常难计算回Key。使用时比如将密码转为 MD5，数据库里存的只有 MD5 所以不怕泄漏，密码明文传到服务器计算 MD5 进而跟数据库匹配的过程由 HTTPS 保证安全。

而平常我用的Hash Table，如C++的STL，map是红黑树，unordered_map是FNV-1a/MurmurHash等低安全性可逆的高效算法，python dict早期也用FNV-1a，现用SipHash（未进行fact check）。

MD5

Message Digest Algorithm 5，字面意思是消息摘要，可以把任何信息转换成128-bit（16 字节）。
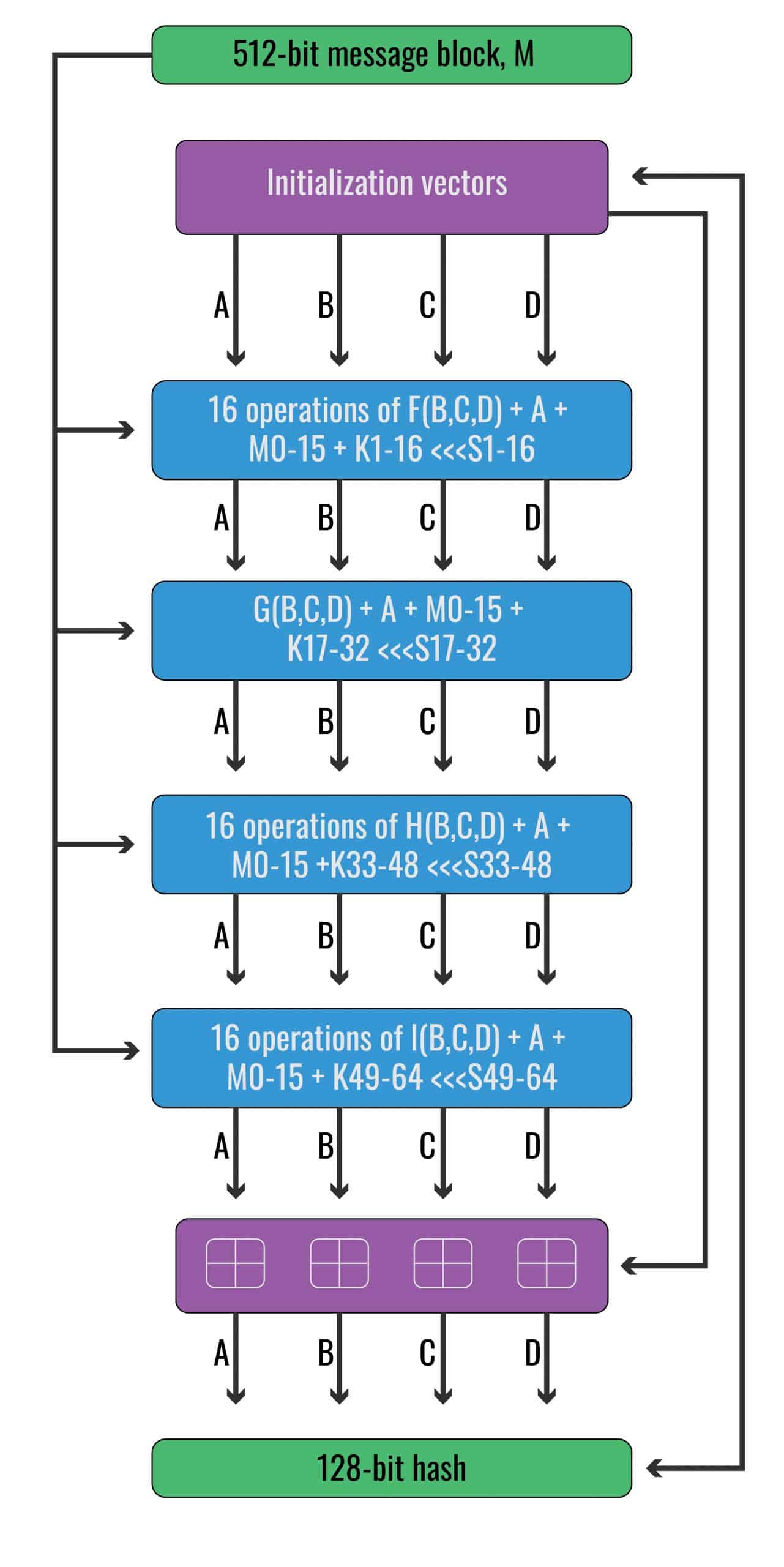
哈希算法的4个步骤：

用填充（Padding）等方式，将数据的二进制形式长度补齐到 ≡ 0 mod 512 整除，然后把数据拆分成一堆 512 bits 的 blocks。

初始化 MD5 缓冲区（都是从右边低字节开始存的，即小端序 Little Endian）：

A = 0x67452301，小端序01234567
B = 0xefcdab89，跟A连着的89abcdef，设置成这个随机初始值纯粹是看起来舒服
C = 0x98badcfe，是B的倒序fedcba98
D = 0x10325476，是A的倒序76543210

每个 512-bit block 计算时都被分成 16 份 32-bit 子块：
- 对 16 个子块共做 4 轮循环，64 次运算；
- 每次运算的公式为 A = B + ((A + F(B,C,D) + M[i] + T[i]) <<< s)，意思是运算时只有寄存器 A 被写了，运算完后（A，B，C，D）寄存器值会右移为（D，Anew，B，C）；
- T 是 64 个 32-bit 常数，M 是 16 份子块，但 4 轮中每轮的索引顺序 i 会变，比如第一轮是0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15，第二轮变成1, 6, 11, 0, 5, 10, 15, 4, 9, 14, 3, 8, 13, 2, 7, 12，s 是每次左移的位数，一切只是为了增加计算复杂度；
- 每轮的操作以下面 4 次运算为例（即整个运算的 1 / 16 部分）：
  A = B + ((A + F(B,C,D) + M[0] + T[0]) <<< s)
  D = A + ((D + F(A,B,C) + M[1] + T[1]) <<< s)
  C = D + ((C + F(D,A,B) + M[2] + T[2]) <<< s)
  B = C + ((B + F(C,D,A) + M[3] + T[3]) <<< s)
- 公式中的 F 在四轮中分别是 F、G、H、I 四个非线性函数，分别是：
| 轮数 | 函数 | 计算公式 |
|—————|———|—————————————————————|
| 0 - 15 | F | $ F(B, C, D) = (B \land C) \lor (\neg B \land D) $ |
| 16 - 31 | G | $ G(B, C, D) = (B \land D) \lor (C \land \neg D) $ |
| 32 - 47 | H | $ H(B, C, D) = B \oplus C \oplus D $ |
| 48 - 63 | I | $ I(B, C, D) = C \oplus (B \lor \neg D) $ |
- 这样经过 4 轮 64 次基于原本信息 M 的运算，得到的（A，B，C，D）四个 32-bit 量再累加到初始值上：
  A = A + 初始 A
  B = B + 初始 B
  C = C + 初始 C
  D = D + 初始 D
- 每一个 512-bit block 都以上一个 block 的（A，B，C，D）为初始值计算，最终得到的（A，B，C，D）4 个 32-bit 变量加起来就是 128-bit MD5。

图中的K就是公式中的T

FNV-1

Fowler–Noll–Vo 分别代表创造算法的三个人。

http://www.isthe.com/chongo/tech/comp/fnv/

hash = offset_basis
for each octet_of_data to be hashed
 hash = hash * FNV_prime
 hash = hash xor octet_of_data
return hash

这里的 octet 就是 byte。
发现其实用的哈希算法非常简单，就是用一个值 hash 乘一个 FNV 质数，之后用这个 hash 跟被哈希信息的每一个字节做异或 XOR，因为 octet_of_data只有 8 位，hash 这个值一般大于 8 位，所以 octet_of_data 在高位补 0，异或操作也不会影响 hash 高于 8 位的部分，相当于之后一直是数据在跟自身异或。

FNV-1a 只是交换了乘 FNV 质数和 XOR 的顺序。

hash = offset_basis
for each octet_of_data to be hashed
 hash = hash xor octet_of_data
 hash = hash * FNV_prime
return hash

用了这么久的 hash table library 们居然只是这么大道至简的算法就能解决存储碰撞，让我有些意外。