
- Python Keywords
- 數學
- Notes
- Lecture 1
- Lecture 2
- Lecture 3
- Lecture 4 計算圖(local gradient and chain rule)
- Lecture 5
- Lecture 6
- Lecture 7
- Lecture 8
- Lecture 9
- Lecture 10
- Lecture 11
- Lecture 12
- Lecture 13
- Lecture 14
- 傳統 Q-learning
- DQN, Deep Q-Learning
- Continue Lecture 14 Reinforcement Learning
- Lecture 15
- Lecture 16
- Lecture 17 Attention and Transformers
- Lecture 18 Self-Supervised Learning
- 降維
- Lecture 19 3D Vision
- Assignments
- Colab
- Regular Expression
- 小知识
- 常遇見bug一覽
Python Keywords
assert
in dictionary
verb
- to say that something is certainly true断言
- to do something to show that you have power主张
- assert your authority/right
in python
definition
The assert keyword is used when debugging code.
用于调试代码。
The assert keyword lets you test if a condition in your code returns True, if not, the program will raise an AssertionError.
如果assert后的条件判断为真,则无事发生继续运行;为假则报错AssertionError。
usage
x = 9527 |
yield
in dictionary
verb
- produce产生
- The process yields oil for industrial use.
- Early radio equipment yielded poor sound quality.
- The experiments yielded some surprising results.
- give up放弃
- Despite renewed pressure to give up the occupied territory, they will not yield.
- bend/break弯折
- His legs began to yield under the sheer weight of his body.
- stop让路
- If you’re going downhill, you need to yield to bikers going uphill.
- Phrasal verb: yield to something
- If you’re going downhill, you need to yield to bikers going uphill.
in python
definition
The yield keyword is used to return a list of values from a function.
用来返回函数值。
Unlike the return keyword which stops further execution of the function, the yield keyword continues to the end of the function.
跟return相比,yield返回值后,函数会继续运行。
When you call a function with yield keyword(s), the return value will be a list of values, one for each yield.
无论yield几次(哪怕只有一次),都会以generator的形式返回。
usage
def test1(): |
可以用for遍历,或以迭代器的方式遍历def test2():
yield 1
yield 2
yield 3
x = test2() #a generator object
print(next(x))
1
print(next(x))
2
print(next(x))
3
for i in test2():
print(i)
1
2
3
generator? what?
iterator first
https://docs.python.org/3/glossary.html#term-iterator
iterator is an object representing a stream of data.
迭代器是个数据流对象。
Repeated calls to the iterator’s __next__() method (or passing it to the built-in function next()) return successive items in the stream. When no more data are available a StopIteration exception is raised instead.
迭代器是這樣一種數據流對象:调用它的“__next__()”方法或用python内置函数“next(iterator)”可以得到它这个流的后继数据,没数据了就抛出StopIteration异常。
根据這裡迭代器的定义,我們就可以自造迭代器类。class MyNumbers:
def __iter__(self):
self.a = 1
return self
def __next__(self):
x = self.a
self.a += 1
return x
myclass = MyNumbers()
myiter = iter(myclass)
print(next(myiter))
1
print(next(myiter))
2
print(next(myiter))
3
这里的iter()也是个内置函数,iter(object)或iter(object, sentinel),接收一個對象返回一個iterator對象。
Without a second argument, object must be a collection object which supports the iterable protocol (the __iter__() method), or it must support the sequence protocol (the __getitem__() method with integer arguments starting at 0).
如果没有sentinel哨兵参数,這裡的object就必须实现__iter__或__getitem__方法。
now generator
https://docs.python.org/3/glossary.html#term-generator
A function which returns a generator iterator. It looks like a normal function except that it contains yield expressions for producing a series of values usable in a for-loop or that can be retrieved one at a time with the next() function.
“generator function”是个包含yield的函数,返回结果是个可以被for循环或python内置函数next()遍历的iterator。
Usually refers to a generator function, but may refer to a generator iterator in some contexts. In cases where the intended meaning isn’t clear, using the full terms avoids ambiguity.
“generator”可能指代函数或迭代器,所以最好说全“生成器函数”或“生成器迭代器”而不只是说“生成器”。
Generator iterator is an object created by a generator function.
Each yield temporarily suspends processing, remembering the location execution state (including local variables and pending try-statements). When the generator iterator resumes, it picks up where it left off (in contrast to functions which start fresh on every invocation).
每个yield都会暂时中止处理,记住位置执行状态(包括局部变量和待处理的try语句)。当生成器迭代器恢复时,它会从上次中断的地方继续执行(与每次调用时都从头开始的函数不同)。
即,调用包含yield的函数会返回一个iterator,每次调用next(iterator)的时候函数就会运行到下一个yield处,python会记录这个yield的位置状态,下次next(iterator)从这里开始运行函数
def test(): |
根据上述官方文档,这里的<class 'generator'>实际上是个”generator iterator”。这里的<class 'function'>实际上是个”generator function”。
generator expression
以前常用的下面这种写法也是个generator,()括号里面写一个循环(必须有括号)。x = (i*i for i in range(10))
print(type(x))
<class 'generator'>
>>> for i in x:
print(i)
0
1
4
9
16
25
36
49
64
81
实际上相当于下面这种写法。def genEx(num):
i = 0
while i < num:
yield i * i
i = i + 1
x = genEx(10)
for i in x:
print(i)
在上面这种只需要print结果的情况里,其实yield可以直接替换成print。
但很多时候不是需要打印而是需要取用这个值,如果把(i * i)存入其他容器也可实现相同功能。yield为这种情况提供了方便。
yield写斐波那契数列
The Fibonacci sequence is the series of numbers where each number is the sum of the two preceding numbers. For example, 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, …def fib(limit): # a generator function
a, b = 0, 1
while (b < limit):
yield b
a, b = b, a + b
x = fib(200) # a generator iterator
for i in x:
print(i)
1
1
2
3
5
8
13
21
34
55
89
144
>>>
numpy dot
矩陣點乘,但向量其實是特殊處理的:
在數學上,點乘需要一個行向量和一個列向量:
但 NumPy 的 1D 陣列已隱含了這個行為。只要兩個 1D 陣列長度相等,它會自動將一個看作「行」,另一個看作「列」,執行點乘運算。因此,不需要手動轉置。
範例
import numpy as np |
如果明確定義行或列向量
如果需要明確區分行向量或列向量,可以使用 2D 陣列來表示:
列向量:v_col = np.array([[1], [2], [3]])(形狀是 3×1)
行向量:v_row = np.array([[1, 2, 3]])(形狀是 1×3)
這時候計算點乘就需要遵守矩陣乘法的規則。
範例:行與列向量操作v_row = np.array([[1, 2, 3]]) # 行向量
v_col = np.array([[4], [5], [6]]) # 列向量
# 行向量乘列向量 (結果是標量)
result = np.dot(v_row, v_col)
print("行向量 * 列向量的結果:")
print(result) # 結果是 [[32]]
# 列向量乘行向量 (結果是矩陣)
result2 = np.dot(v_col, v_row)
print("列向量 * 行向量的結果:")
print(result2) # 結果是 3x3 矩陣
輸出:行向量 * 列向量的結果:
[[32]]
列向量 * 行向量的結果:
[[ 4 8 12]
[ 5 10 15]
[ 6 12 18]]
numpy裡想取一行是array[i],想取一列是array[:,j]。
chatgpt輔助寫代碼實在是太好用了,語法這方面絕對的百科全書。
lambda
lambda 是 Python 中用来创建匿名函数(没有名字的函数)的一种表达式。它非常简洁,但功能强大,适合用在一些简单的场景。
基本语法
lambda 参数1, 参数2, ...: 表达式 |
- 参数:可以有多个参数,类似于常规函数定义。
- 表达式:只能包含一个表达式,表达式的计算结果即为返回值。
示例
- 简单的用法
# 普通函数定义
def add(x, y):
return x + y
# lambda表达式
add_lambda = lambda x, y: x + y
print(add(3, 5)) # 输出 8
print(add_lambda(3, 5)) # 输出 8 - 作为内联函数
常用在需要短小函数的场景,例如 map()、filter()、sorted() 等。- 跟map()配合
nums = [1, 2, 3, 4]
squared = map(lambda x: x ** 2, nums)
print(list(squared)) # 输出 [1, 4, 9, 16] - 与filter()配合
nums = [1, 2, 3, 4, 5]
even = filter(lambda x: x % 2 == 0, nums)
print(list(even)) # 输出 [2, 4] - 跟sorted()配合
words = ["apple", "banana", "cherry"]
sorted_words = sorted(words, key=lambda x: len(x))
print(sorted_words) # 输出 ['apple', 'cherry', 'banana']
- 跟map()配合
- 作为函数参数
可以直接将 lambda 函数传递给其他函数作为参数。def apply_function(func, value):
return func(value)
result = apply_function(lambda x: x * 2, 10)
print(result) # 输出 20
优缺点
优点:
- 简洁,适合定义简单逻辑。可以轻松传递小函数。
缺点:
- 只能写单一表达式,功能有限。
- 可读性较差,复杂逻辑建议使用 def 定义常规函数。
使用建议:
- 当逻辑非常简单且不会重复使用时,用 lambda。
- 复杂逻辑或需要调试时,使用 def 明确定义函数。
广播broadcast
| A.shape | B.shape | Resulting Shape | 说明 |
|---|---|---|---|
| (3, 4) | (3, 4) | (3, 4) | 相同形状,逐元素操作 |
| (3, 4) | (1, 4) | (3, 4) | B 的第 0 维度广播为 3,变成(3, 4) |
| (3, 4) | (4,) | (3, 4) | B 增加维度后广播为 (1, 4),再把第 0 维广播为(3, 4) |
| (3, 1, 4) | (1, 2, 4) | (3, 2, 4) | 高维度逐维广播 |
| (3, 4) | () | (3, 4) | 标量广播为 (3, 4) |
| (3, 4) | (2, 4) | Error | 形状不兼容,无法广播 |
广播其实就是把两个矩阵补成一样大小。
注意⚠️:
- 广播的结果只是虚拟扩展,并不真的复制数据,因此它的内存和计算效率都很高。
如果不确定广播的结果,可以使用 np.broadcast_shapes 或 np.broadcast_to 来检查或预览。
# 检查广播后形状
np.broadcast_shapes((3, 4), (1, 4)) # 输出 (3, 4)标量:
A = np.ones((3, 4))
B = 2 # 标量
C = A + B # B 会广播为 (3, 4) 进行相加- 高维度例如(3, 1, 4)和(1, 2, 4)
- 第 0 维:3 和 1 -> 广播为 3。
- 第 1 维:1 和 2 -> 广播为 2。
- 第 2 维:4 和 4 -> 保持不变。
- 最终广播结果为 (3, 2, 4)
A = np.ones((3, 1, 4))
B = np.ones((1, 2, 4))
C = A + B # 广播为 (3, 2, 4)
random
| 特性 | np.random.rand |
np.random.randn |
|---|---|---|
| 生成分布 | 均勻分布(Uniform distribution) | 標準正態分布(Standard normal distribution, 均值 0,方差 1) |
| 數值範圍 | $[0, 1)$ | 理論上為 $(-\infty, +\infty)$,但集中於約 $[-3, 3]$ |
| 輸出數值類型 | 浮點數(float) | 浮點數(float) |
| 用途 | 模擬隨機比例、概率等均勻分布的數據 | 模擬中心為 0 且有波動的隨機數據,適用於神經網絡初始化等場景 |
| 場景 | np.random.rand 用法 |
np.random.randn 用法 |
|---|---|---|
| 模擬隨機概率 | 用於生成隨機概率數據,例如蒙特卡洛模擬 | 不適用 |
| 數據增強 | 隨機調整數據(添加隨機偏差) | 添加噪聲,用於模型訓練的數據增強 |
| 神經網絡初始化 | 初始化介於 $[0, 1)$ 的權重 | 初始化符合正態分布的權重,中心為 0,標準差為 1 |
| 隨機測試 | 在 $[0, 1)$ 中隨機生成測試數據 | 模擬符合正態分布的隨機測試數據 |
numpy/
├── random/ # numpy.random 模組
│ ├── Generator # 現代化的隨機數生成器 (建議用)
│ ├── RandomState # 傳統的隨機數生成接口
│ ├── rand() # 均勻分布隨機數 (RandomState 方法)
│ ├── randn() # 標準正態分布隨機數 (RandomState 方法)
│ ├── randint() # 整數隨機數生成
│ ├── normal() # 通用正態分布隨機數生成
│ ├── uniform() # 通用均勻分布隨機數生成
│ ├── seed() # 設置隨機種子
│ ├── …
| 方法 | 功能 |
|---|---|
np.random.rand |
生成均勻分布的隨機數,範圍為 $[0, 1)$。 |
np.random.randn |
生成標準正態分布(均值為 0,標準差為 1)的隨機數。 |
np.random.randint |
生成隨機整數,可以指定範圍和大小。 |
np.random.uniform |
生成均勻分布的隨機數,可以指定範圍,例如 $[a, b)$。 |
np.random.normal |
生成正態分布的隨機數,可以指定均值和標準差。 |
np.random.choice |
從給定的序列中隨機選取元素,可以指定抽樣數量和是否放回。 |
np.random.shuffle |
就地打亂給定的數組(改變原數組順序)。 |
np.random.permutation |
返回給定數組的隨機排列(不改變原數組)。 |
np.random.seed |
設置隨機數生成器的種子,用於保證實驗的可重現性。 |
np.random.beta |
生成 Beta 分布隨機數。 |
np.random.binomial |
生成二項分布隨機數。 |
np.random.poisson |
生成泊松分布隨機數。 |
np.random.exponential |
生成指數分布隨機數。 |
seed = 231 # 如果不設定 seed,兩個 random 每次的值就都不一樣,設定了就永遠一樣 |
生成所需區間的隨機數,比如[a, b):$(b - a)random + a$(b - a) * np.random.rand() + a
(b - a) * torch.rand(1, 1) + a
double rand_range(double a, double b) { |
星號*
np.random.rand(x.shape)是不行的,np.random.rand(x.shape[0], x.shape[1], x.shape[2])這樣可以,或者用*。
np.random.rand(*x.shape),在這裡, 是一個*解包運算符(unpacking operator),它將 x.shape 元組的每個元素作為獨立參數傳入。
* 是 Python 的解包運算符,主要用來將 可迭代對象(如列表、元組)展開為單獨的元素。
在函數調用中,* 可以用來將列表或元組中的元素作為多個獨立的參數傳入函數。
torch.rand(*size, *, generator=None, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False, pin_memory=False) → Tensor
pad
numpy.pad(array, pad_width, mode='constant', **kwargs) |
| 参数 | 说明 | 示例 |
|---|---|---|
array |
要填充的数组,支持任意维度 | np.array([1, 2, 3]) |
pad_width |
填充宽度,可以是整数、元组或元组列表 | 2 (所有维度前后各填充 2 个);((1, 1), (2, 2))(每维单独指定) |
mode |
填充模式,常用模式如下: | |
'constant' |
填充固定值,默认值为 0,可通过 constant_values 指定 |
np.pad([1, 2], 2, mode='constant', constant_values=9) -> [9, 9, 1, 2, 9, 9] |
'edge' |
用边界值填充 | np.pad([1, 2], 2, mode='edge') -> [1, 1, 1, 2, 2, 2] |
'symmetric' |
对称填充(包括边界) | np.pad([1, 2], 2, mode='symmetric') -> [2, 1, 1, 2, 1, 1, 2] |
'reflect' |
镜像填充(不包括边界) | np.pad([1, 2], 2, mode='reflect') -> [2, 1, 2, 1, 2, 1] |
'wrap' |
环绕填充 | np.pad([1, 2, 3], 2, mode='wrap') -> [3, 1, 2, 3, 1, 2, 3, 1] |
| 其他参数 | 根据模式指定额外参数 | |
constant_values |
在 constant 模式下指定填充值 |
np.pad([1, 2], 2, mode='constant', constant_values=5) -> [5, 5, 1, 2, 5, 5] |
array改變形狀
transpose和moveaxis
N, C, H, W = 2, 3, 4, 5 |
本质上,moveaxis 是 transpose 的封装,简化了多维轴变换的操作,但效果和 transpose 相同。
reshape
np.array_equal(x.transpose(1, 0, 2, 3), x.reshape(C, N, H, W)) |
reshape:改变形状,不改变数据的顺序。它不能实现轴的重新排列效果。
transpose:调整轴的顺序,可能导致数据的逻辑顺序发生变化。
moveaxis:更灵活的轴变换,与 transpose 作用相同。
import numpy as np |
array擴展
np.tile(A, reps) 用于重复数组,将输入数组沿指定维度扩展成更大的数组。
- A:输入数组。
- reps:整数或元组,表示每个维度重复的次数。
import numpy as np
# 1維重複3次
print(np.tile([1, 2], 3)) # [1 2 1 2 1 2]
print(np.tile([[1, 2], [3, 4]], (2, 3))) # 1維(行)重複兩次,2維(列)重複三次
# [[1 2 1 2 1 2]
# [3 4 3 4 3 4]
# [1 2 1 2 1 2]
# [3 4 3 4 3 4]]
concatenation拼接
使用 + 操作符(對於列表)或 numpy.concatenate() 函數(對於數組)。
list直接相+。
torch裡跟numpy的操作是幾乎一樣的,所以很方便。
import numpy as np |
torchvision.transforms
One of our former instructors, Justin Johnson, made an excellent tutorial for PyTorch.
You can also find the detailed API doc here. If you have other questions that are not addressed by the API docs, the PyTorch forum is a much better place to ask than StackOverflow.
import torchvision.transforms as T |
Compose()
將多個圖像預處理操作組合成一個序列,就是打包預處理。
比如其中第一個T.ToTensor()就是把圖像轉成Tensor數據類型。另外還可以做Resize和CenterCrop之類的操作。查上面的libraries/torchvision文檔。
Normalize()
torchvision.transforms.Normalize(mean, std) |
- mean:是一个列表或元组,包含每个通道的均值(例如,对于 RGB 图像,可以是
[R_mean, G_mean, B_mean])。 - std:是一个列表或元组,包含每个通道的标准差(例如,对于 RGB 图像,可以是
[R_std, G_std, B_std])。
每個通道分別減去所有圖像的統計量。
torch.nn.Sequential()
跟上面的Compose()很像就一塊說了。
model = torch.nn.Sequential( |
這個是打包網絡層方便前後向計算。
DataLoader
from torch.utils.data import DataLoader |
torchvision.datasets.CIFAR10加載數據集:
- root時存儲路徑,如果沒有且download=True會自動下載,
- train=True加載訓練集(data_batch_1/2/3/4/5),False加載測試集(test_batch)
- transform就是預處理
這裡如果不 ToTensor() 返回的不是 Python 列表 (List) ,也不是numpy.ndarray,是 PIL.Image.Image 對象。
- 数据转换 是在 Dataset 对象创建时完成的(通过 transform)。
- 数据加载和批处理 是在 DataLoader 中进行的。
PIL/Pillow
from PIL import Image |
PIL 是 Python Imaging Library,Initial release 是1995年,Pillow 是 2010 年 forked 這個 PIL repository 並支持 Python 3.x 的繼任者。
為什麼需要DataLoader?
上面用 torchvision.datasets 用 PIL 讀取數據並轉為 Tensor之後,用DataLoader轉為torch.utils.data.dataloader.DataLoader。
這裡不用 sampler 用 shuffle=True 的話是打亂整個數據集,跟 SubsetRandomSampler 也差不多,都是不放回的隨機抽樣。全部輸入一遍就是一個epoch,一個minibatch是一個iteration。loader_train = DataLoader(cifar10_train, batch_size=64, sampler=sampler.SubsetRandomSampler(range(NUM_TRAIN)))
for data, target in loader_train:
print(data.device) # 检查每个批次数据的设备,返回“cpu”
break # 只查看第一个批次
其中,cifar10_train 是 Tensor 原數據集,batch_size 是每個 minibatch 的大小,sampler 是採樣 minibatch 的方法,這裡是從索引 0 到 49000 隨機取 64 個。
- 提前分好 minibatches 比較方便,assignment 1/2 裡的 /cs231n/solver 都是在
_step()裡用batch_mask = np.random.choice(num_train, self.batch_size)現取; - DataLoader 負責分批把數據加載到內存,節省 CPU Memory;
- 支持多線程並行加載數據,用
DataLoader(..., num_workers=4)可以加速讀數據;
PyTorch vs. Numpy
在Lecture 8討論過Pytorch相比Tensorflow除了一個Dynamic vs. Static的優勢之外,還有就是類似numpy所以上手快。
所以在這整理一點兒用到過的等價操作,以供查閱,以防混淆。
| Pytorch | Numpy | |
|---|---|---|
| torch.Tensor | numpy.ndarray | 相似數據類型 |
| Tensor.view() | ndarray.reshape() / numpy.reshape() | 數據結構內置 |
| torch.arange() | range() | 前者生成Tensor後者生成list |
| Tensor.matmul() | ndarray.dot() | 矩陣乘 Matrix Multiplication,python 3.5後可以用 @,相當於 matmul 和 dot 的語法糖。对于高维张量:执行广播规则,然后对最后两个维度进行矩阵乘法。 |
| Tensor.dot() | ndarray.dot() | 只能接受兩個一維向量計算內積 |
| Tensor.mm() | ndarray.dot() | 只能接受兩個二維矩陣算矩陣乘法,但因為底層實現比matmul()簡單所以大概更快 |
| * | * | 廣播逐元素乘 broadcast elementwise |
| torch.rand / torch.randn | numpy.random.rand / numpy.random.randn | 討論過numpy,torch用法跟numpy有點細微區別在下面補充一下吧 |
| s.gather(1, y.view(-1, 1)).squeeze() | s[np.arange(N), y] | Tensor[range(len(y)), y]也可以啊…好像不需要gather這個語法了 |
| torch.tensor(), torch.Tensor() | np.array() np.asarray() | 轉類型 |
| torch.cat((A,B),dim=0) | np.concatenate((A,B),axis=0) | 拼接 |
| Tensor.permute() | numpy.transpose() | 轉置,之前還總結過跟moveaxis的區別 |
這次能一個月做完也多虧了 chatgpt,2022 年末在商湯時 chatgpt 突然爆火,當時如果能用熟的話也不至於那麼菜。
seed = 231 # 如果不設定 seed,兩個 random 每次的值就都不一樣,設定了就永遠一樣 |
requires_grad和Pytorch裡的computational graph
w = torch.randn(shape, device=device, dtype=dtype) * np.sqrt(2. / fan_in) |
初始化 weights 的 requires_grad 應該用這種寫法,如果寫到torch.randn裡是錯誤的。w = torch.randn(shape, device=device, dtype=dtype, requires_grad=True) * np.sqrt(2. / fan_in)
# tensor([[0.6324]], device='cuda:0', grad_fn=<MulBackward0>)
當輸出顯示requires_grad=True的時候表示 w 在計算圖裡沒有反向傳播的 gradient function,grad_fn=<MulBackward0>表示一個計算圖的節點。
這裡的 grad_fn (gradient function) 是一個指向反向傳播函數的引用,MulBackward0 表示這個反向傳播的 node 用逐元素乘 gradient function,除此之外還有 MatMulBackward (矩陣乘) / AddBackward (加) / DivBackward (除) 等。(其中 0 不知道代表什麼,測試過重複乘並不會變成 1。)
* np.sqrt(2. / fan_in)這個操作相當於在 計算圖 裡加入了一個 乘法 節點(torch.autograd),反向傳播的時候會錯誤地給 dw 再乘上這個初始化操作* np.sqrt(2. / fan_in)。
關於torch.no_grad()
首先捋一遍pytorch梯度更新過程:
output = model(x)前向傳播,生成計算圖;loss = torch.nn.CrossEntropyLoss(output, label)計算損失;loss.backward計算所有requires_grad=True的節點構成的計算圖,用每一個node的grad_fn計算梯度,存到參數Tensor的.grad屬性(attribute)裡面;- 更新參數(nn.Module / nn.Sequential): 或者像assignment裡的barebone一樣手動操作:
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate) # 定義優化器
optimizer.step() # 用每個參數的.grad更新
optimizer.zero_grad() # 清空.grad梯度with torch.no_grad():
for w in params:
w -= learning_rate * w.grad
# Manually zero the gradients after running the backward pass
w.grad.zero_()
在不需要反向傳播的時候就需要 torch.no_grad() 阻止 output = model(x) 生成計算圖,以節省推理時的內存和時間。
| API | Flexibility | Convenience |
|---|---|---|
| Barebone | High | Low |
nn.Module |
High | Medium |
nn.Sequential |
Low | High |
Barebone:output = torch.nn.functional.conv2d(input, weight, bias=None, stride=1, padding=0, dilation=1, groups=1) → Tensor
nn.Module:conv = torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros', device=None, dtype=None)
output = conv(input)
除了 optimizer 有區別,用 nn.Module/nn.Sequential 這樣的寫法不用在外部定義繁瑣的 weights 再傳進去。
傳參:可變對象 vs. 不可變對象
不像 C 裡面傳參只能通過傳變量指針的方式 void fn(int *var) 在函數內部修改變量,python 有兩種對象:
- 可變對象 (Mutable objects): list, dict 或是被訓練的 torch.nn.Module 都是可變對象,在函數內修改後函數外也可以看到變化;
- 不可變對象 (Immutable objects): int, float, tuple, str 跟 C 裡一樣,函數裡使用的時候其實是創造了一個新對象,函數內修改不會影響到函數外的變量本身。
def fn(aaa):
aaa.append(1)
return
bbb = [0]
fn(bbb) # a list is a mutable object
print(bbb)
[0, 1]
def fn(ccc):
ccc += 1
return
ddd = 0
fn(ddd) # an integer is an immutable object
print(ddd)
0
所以訓練完 torch.nn.Module 子類 對象 model 之後是不需要返回的,函數內已經改變了 model 的 parameters 為優化後結果。
這裡的 Module 父類除了 forward() 之外還有 parameters() 可以返回模型中所有可學習的參數。
model.eval()
model.eval() 是为了将模型设置为评估模式,主要影响 Dropout 和 BatchNorm 层。
- 在评估模式下,Dropout 层不会丢弃神经元,而是使用所有神经元的输出;
- BatchNorm 层会使用训练时计算的全局均值和方差。
訓練時要調到 model.train() 模式。
零碎pytorch
torch.flip和transforms.RandomHorizontalFlip 和 transforms.RandomVerticalFlip有兩種flip。
transforms.RandomApply([operation], p=0.5)可以讓 torchvision.transforms 在某個概率下執行,不知道ToTensor()這種和nn.Linear()可不可以生效。
grayscale灰度圖像轉換公式:Y=0.2989×R+0.5870×G+0.1140×B,
transforms.Grayscale(num_output_channels=1),設置成 3 的話 3 個通道都是一樣的灰度值。ass裡是設成 3 了。
cosine similarity又叫 normalized dot product 歸一化點積。
torch.masked_select(input, mask, *, out=None) 應用mask後會把mask=True的元素平鋪成一個 1 維 tensor 返回。
torchvision.utils.make_grid(images) 把多張圖拼成一個大圖。
keepdim=True
- sum()
- mean()
- std()
- max()
- min()
- prod()
- argmax()
- argmin()
以上這些函數都可以 keepdim,比如對 N, D 維度的 tensor x 做 x.sum(dim=1) 結果是 torch.Size([10]) 而 x.sum(dim=1, keepdim=True) 結果是 torch.Size([10, 1]) 。
最好想清楚廣播或者後續計算需不需要保持維度一致,ass3的simclr的contrastive_loss.py裡面sim_positive_pairs就因為這個結果錯了。
使用預訓練resent
用simclr的代碼做例子。
import torch |
用 pytorch 真的很簡單。
數學
矩阵计算加速
反直觉的简化公式。
这些公式的反直觉点在于:
- 避免直接操作整个矩阵或高维数据,通过预处理(如点积、模长)简化计算。
- 利用代数性质减少重复计算,如平方展开、trace 操作。
- 通过广播机制和维度扩展,实现高效并行计算。
1. L2距离矩阵
L2 中的 “L” 是 “norm” 的缩写来源,表示范数(norm)的符号约定。“L” 最早来源于法语数学文献中用于 Lebesgue 空间($L^p$-spaces)的符号,它现在广泛用于表示函数和向量范数。
问题:给定两个矩阵 $A \in \mathbb{R}^{m \times n}$ 和 $B \in \mathbb{R}^{p \times n}$,计算两组向量之间的欧几里得距离矩阵 $D$,形状为 $(m, p)$。
公式:
简化:
解释:
- 利用 $A \cdot B^T$ 点积高效计算向量间的关系。
KNN计算(500,3072)和(5000,3072)得到(500,5000)的两两图片距离矩阵时,有两种做法:
第一种:
I. 直接通过广播计算一个 $(500, 3072) - (5000, 3072)$ 得到 $(500, 5000)$ 的矩阵?
我们需要计算一个矩阵 $\mathbf{C} \in \mathbb{R}^{500 \times 5000}$,其中每个元素为:
或展开为:
直接广播计算的步骤
输入矩阵形状
- $\mathbf{A} \in \mathbb{R}^{500 \times 3072}$
- $\mathbf{B} \in \mathbb{R}^{5000 \times 3072}$
扩展维度
- 将 $\mathbf{A}$ 扩展为 $(500, 1, 3072)$:
- 将 $\mathbf{B}$ 扩展为 $(1, 5000, 3072)$:
广播相减
- 利用广播机制直接相减,结果是形状为 $(500, 5000, 3072)$ 的 3D 矩阵:
计算平方差
- 对最后一个维度(即 3072)计算平方和,得到形状为 $(500, 5000)$ 的矩阵:
完整代码实现
import numpy as np |
问题
“直接广播可能导致内存不足”的原因是 广播机制会在内存中创建一个扩展后的高维临时数组。
对于形状为 $ (500, 3072) $ 的矩阵 $ A $ 和 $ (5000, 3072) $ 的矩阵 $ B $:
- 扩展后它们会形成 $ (500, 1, 3072) $ 和 $ (1, 5000, 3072) $。
- 相减后生成一个 $ (500, 5000, 3072) $ 的 3D 数组。
这个 3D 数组需要存储 $ 500 \times 5000 \times 3072 $ 个浮点数,占用约 76 GB(若每个浮点数占 8 字节)。
对于大规模数据,内存无法承受,因此直接广播操作会报错或导致性能问题。
使用范数分解公式避免构造高维中间数组,可以极大节省内存。
第二种:
II. 优化方法:使用范数分解公式
由于直接广播会创建一个巨大的 $(500, 5000, 3072)$ 的临时数组,可能导致内存不足,我们可以利用范数分解公式优化计算。
公式展开为:
优化后的步骤
预先计算每行向量的平方和:
- 对于 $\mathbf{A}$,计算 $|\mathbf{A}[i, :]|^2$:
- 对于 $\mathbf{B}$,计算 $|\mathbf{B}[j, :]|^2$:
计算点积:
合并结果:
优化代码实现
# 计算每行向量的平方和 |
两种方法对比
| 方法 | 内存占用 | 计算速度 | 适用场景 |
|---|---|---|---|
| 直接广播相减 | 高(需要创建 3D 数组) | 简单实现 | 小规模矩阵 |
| 范数分解公式 | 低(避免创建 3D 数组) | 更高效 | 大规模矩阵 |
2. 余弦相似度矩阵
问题:给定矩阵 $A$ 和 $B$,计算两组向量的余弦相似度矩阵:
简化:
解释:
- 先计算点积 $A \cdot B^T$。
- 再将每行的模长预计算为一个列向量,最后进行广播除法。
3. 矩阵 Frobenius 范数的平方
Frobenius 范数:
如果需要计算两个矩阵 $A$ 和 $B$ 之间的差的 Frobenius 范数:
解释:
- 通过展开 $| A - B |_F^2$,简化计算,避免构造 $A - B$。
4. 交叉熵损失的高效计算
交叉熵损失公式:
如果 $y$ 是 one-hot 编码的标签,交叉熵可以简化为直接取预测的正确类别的概率对数:
解释:
- 不需要计算 $y$ 和 $\hat{y}$ 的逐元素乘积,只需取索引值。
5. 矩阵的平方和(双循环的优化)
直接计算矩阵 $A \in \mathbb{R}^{m \times n}$ 中每对行向量的平方和:
可以化简为:
解释:
- 避免显式计算所有对的组合,通过提前计算模长和点积直接构造。
6. 矩阵乘法优化(维度分解)
如果需要计算 $C = A^T A$,其中 $A \in \mathbb{R}^{m \times n}$,可通过分块减少乘法次数:
- 普通算法时间复杂度为 $O(m^2 n)$。
- 利用分块或对称性质,可以优化为 $O(m^2)$。
矩陣求導,要轉置
矩阵C=AB那C对A的导数是B的转置,C对B的导数是A的转置。
假设 $C = A \cdot B$,则矩阵求导结果如下:
$C$ 对 $A$ 的导数:
因为 $A$ 的每个元素对 $C$ 的每个元素的贡献是通过 $B$ 的列影响的。
$C$ 对 $B$ 的导数:
因为 $B$ 的每个元素对 $C$ 的每个元素的贡献是通过 $A$ 的行影响的。
例子验证
假设:
计算 $C = A \cdot B$:
对 $A$ 求导(结果为 $B^T$):
对 $B$ 求导(结果为 $A^T$):(在矩陣乘法裡,A的1和2,只會受到B的5和7影響;對A的3和4來說只有B的6和8會影響結果,所以正好轉置過來)
商的求导法则
如果函数为 $\frac{u(x)}{v(x)}$,其导数公式是:
例子 1: $ \frac{x}{x+1} $ 的导数
设 $u = x$,$v = x+1$:
- $u’ = 1$,$v’ = 1$。
代入公式:
例子 2: $ \frac{x^2}{x+2} $ 的导数
设 $u = x^2$,$v = x+2$:
- $u’ = 2x$,$v’ = 1$。
代入公式:
化简:
幂函数的求导公式
如果 $f(x) = x^n$,对 $x$ 求导,我们直接应用幂函数的求导公式:
这是基本的导数公式,其中:
- $n$ 是常数,
- $x^{n-1}$ 是 $x$ 的幂次降低1后的表达式。
例如:
- 若 $f(x) = x^3$,则 $f’(x) = 3x^2$;
- 若 $f(x) = x^{-2}$,则 $f’(x) = -2x^{-3}$;
- 若 $f(x) = x^{1/2}$,则 $f’(x) = \frac{1}{2}x^{-1/2} = \frac{1}{2\sqrt{x}}$。
正則項的偏導
对于正则化项:
$
\text{Regularization} = \text{reg} \cdot \left(|W_1|_F^2 + |W_2|_F^2\right)
$
计算对各参数的偏导:
对 $W_2$:
$
\frac{\partial \text{Regularization}}{\partial W_2} = 2 \cdot \text{reg} \cdot W_2
$对 $b_2$:
$
\frac{\partial \text{Regularization}}{\partial b_2} = 0
$
因为正则化不包含偏置。对 $W_1$:
$
\frac{\partial \text{Regularization}}{\partial W_1} = 2 \cdot \text{reg} \cdot W_1
$对 $b_1$:
$
\frac{\partial \text{Regularization}}{\partial b_1} = 0
$
总结:
- 正则化项仅对权重 $W_1$ 和 $W_2$ 起作用,偏导为 $2 \cdot \text{reg} \cdot W$。
- 偏置 $b_1$ 和 $b_2$ 的偏导为零。
- 對 $dx$ 的偏導也是0,梯度往前傳遞是靠 $dx$ 。
b1不是input_dim,b2不是hidden_dim:
self.params['W1'] = np.random.normal(loc=0.0, scale=weight_scale, size=(input_dim, hidden_dim)) |
Adam優化版
如果你看到的 Adam 公式版本中没有显式的 $t$(时间步),那可能是省略了 $t$ 的具体表示形式。但实际上,Adam 的完整公式中 $t$ 隐含在动量更新和偏差校正因子中。以下是 Adam 优化器的完整公式:
一阶动量(梯度的指数加权平均):
二阶动量(梯度平方的指数加权平均):
偏差校正(修正初期估计的偏向零问题):
参数更新:
这里的 $t$ 是显式表示每个时间步的迭代次数,用于偏差校正因子的计算。在实际实现中,时间步通常由代码中的循环或计数器隐式管理,因此部分文档可能会省略 $t$ 的具体表示。
如果你看到的公式中没有偏差校正因子的部分,可能是简化版本,忽略了初期动量估计偏差的影响。这种版本常用于直观解释或早期实现中。
beta ** t,t越大m_hat就越大,防止一開始過小的問題。
对数的商的性质
其中 $a > 0, b > 0$,对数的底可以是任意正数(通常是 10 或 $e$,但不能是 1)。
BN的梯度
1. Batch Normalization (BN) 层的梯度计算
Batch Normalization 的反向传播较为复杂,因为它涉及多个步骤的链式法则计算。下面是完整推导过程和实现思路:
BN 前向传播公式
给定输入 $x_i$:
- 计算均值和方差:
- 标准化:
- 应用缩放和平移(可学习参数 $\gamma$ 和 $\beta$):
BN 反向传播公式
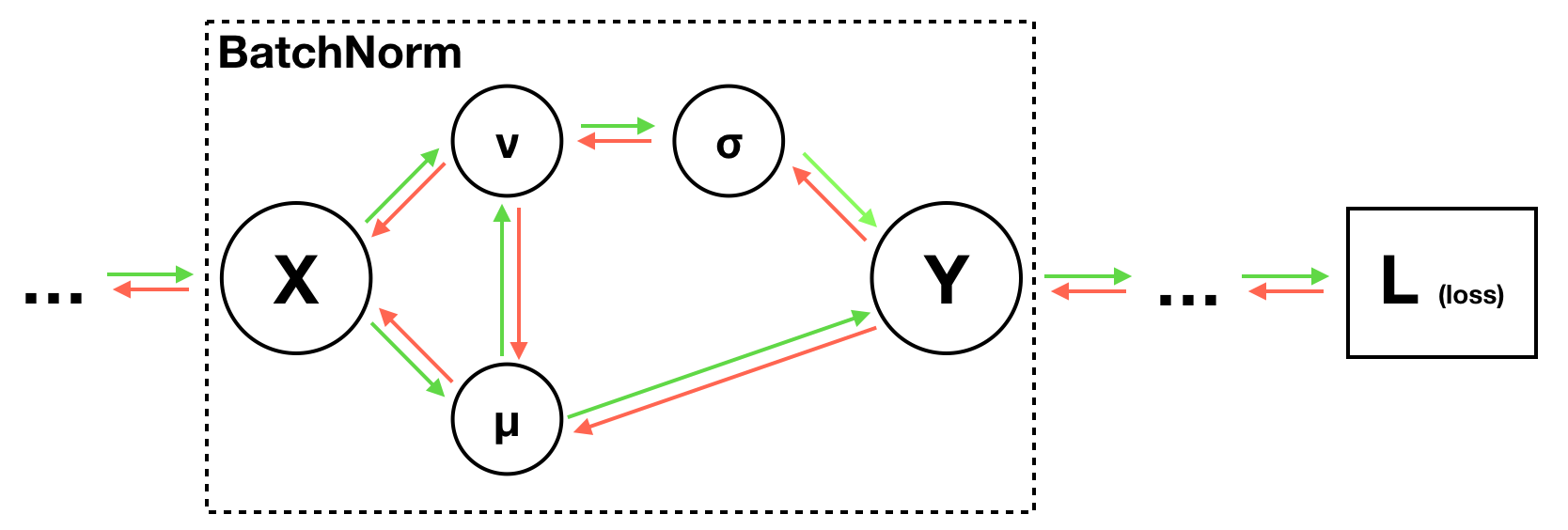
1. 梯度传播关系
BN 的输出 $y_i$ 的梯度通过链式法则回传:
因此,关键在于计算 $\frac{\partial y_i}{\partial x_i}$。
2. 分步骤求解
对 $\gamma$ 和 $\beta$ 的梯度:
对 $\hat{x}_i$ 的梯度:
3. 對 $ x_i $ 的梯度需要$\frac{\partial \mu}{\partial x_i}, \frac{\partial v}{\partial x_i}, \frac{\partial \sigma}{\partial v}, \frac{\partial Y}{\partial \sigma}$, and $\frac{\partial Y}{\partial \mu}$
計算圖裡的var和mu那條關係可以忽略,可以不走那邊。
$\frac{\partial Y}{\partial \sigma}$, $\frac{\partial Y}{\partial \mu}$其實算的是$\gamma \cdot \frac{\partial \hat{x_i}}{\partial \sigma}$, $\gamma \cdot \frac{\partial \hat{x_i}}{\partial \mu}$。
公式提要:
mean對x的導數:
$\text{mean} = \frac{1}{n} \sum_{i=1}^n x_i$,对 $x_k$ 求导时:方差的導數$\frac{\partial v}{\partial x_i}$:
發現除了$\frac\partial{\partial x_i}, (x_i-\mu)^2=2(x_i - \mu)$都是0,所以
或者把mean也展開就是
standard deviation標準差對variance方差的導數很好求,就是幂函数的求导公式,$\sigma=\sqrt{v+\epsilon}$導數是$\sigma’=\frac{1}{2\sqrt{v+\epsilon}} = \frac{1}{2\sigma}$。
chatgpt說:計算$\frac{x-mean}{std}$對mean和std的偏導時,雖然mean和std都是依賴於x的統計特性,但算一個偏導可以把另一個看作常數:
- $\gamma \cdot (\frac{\partial \hat{x_i}}{\partial \sigma} = \frac{-1}{std})$
- $\gamma \cdot (\frac{\partial \hat{x_i}}{\partial \mu} = -\frac{x - mean}{std^2} = -\frac{x_i-\mu}{std^2})$ 他媽的發現錯誤原因是這倆求反了,下面也代入反了,一下午打水漂。chatgpt說的是對的,計算後證明這倆反過來算對了。但事實證明不對,而且沒理解好鏈式法則,沒有加上直接項。正確的理解在下面,按下面的公式,這裡其實改寫成$L = f(\Phi, \Psi, \Omega), \Phi = a(x) = x, \Psi = b(x) = mean, \Omega = c(x) = std, f(\Phi, \Psi, \Omega) = \frac{\Phi - \Psi}\Omega$。參考https://kevinzakka.github.io/2016/09/14/batch_normalization/ 1.沒有把另外一個統計量當作常數;2.對$\mu$和$\sigma$的任何求導,根據下文一個變量的導數和他本身維度通常一致,結果應該是個scalar或者vector,所以要求和,我的計算都漏了求和!重新算:
$\frac{\partial Y}{\partial x_i} = \frac{\partial Y}{\partial \hat{x_i}}\frac{\partial \hat{x_i}}{\partial x_i} + \frac{\partial Y}{\partial \sigma}\frac{\partial \sigma}{\partial v}\frac{\partial v}{\partial x_i} + \frac{\partial Y}{\partial \mu}\frac{\partial \mu}{\partial x_i}$ 還差標題的后倆:
- $\frac{\partial Y}{\partial \sigma} = \gamma \cdot \sum_{i=1}^N upstream \cdot \frac{\partial \hat{x_i}}{\partial \sigma}$ 中,
$\frac{\partial v}{\partial \mu}$:
方差公式:
对 $\mu$ 求导数:
将求导运算移入求和符号中:
求单项的导数:
注意到 $\frac{\partial}{\partial \mu} (x_i - \mu) = -1$,代入得:
将结果代入整体公式:
提取常数项 $-2$:
根据均值的定义,$\sum_{i=1}^N (x_i - \mu) = 0$,因为均值是数据的平衡点。
$\frac{\partial Y}{\partial \mu} = \gamma \cdot \sum_{i=1}^N upstream \cdot \frac{\partial \hat{x_i}}{\partial \mu}$ 中,方差和標準差sigma其實也是mean的函數$v=\frac{1}{N}\sum_{k=1}^N (x_k-\mu)^2$,所以根據復合函數鏈式法則:
最後,$\frac{\partial \hat{x_i}}{\partial x_i} = \frac{1}{\sigma}$。
最終,
化簡:
其中的$\gamma \cdot upstream$其實可以合成為$\hat{upstream}$,測試的speedup是3.69x。另外layernorm就把所有的axis=0改成axis=1即可。
論文裡求過偏導了,但算起來比較慢。這樣用計算圖鏈式法則一步到位,雖然手算慢,但電腦運算快。
Note that the batch normalization paper suggests a different test-time behavior: they compute sample mean and variance for each feature using a large number of training images rather than using a running average. For this implementation we have chosen to use running averages instead since they do not require an additional estimation step; the torch7 implementation of batch normalization also uses running averages.
掙扎了大半天時間梯度終於算對了,感謝UCB哥的推導,最後發現了兩個問題,1.我居然忘記算upstream(dout)了,2.求和的對象太關鍵了,求和的範圍是$\mu$,$\sigma$的偏導範圍決定的。這種公式問chatgpt它還是算不明白的,雖然它的結果通常沒錯。
四年前倒在這,直到現在還是不能像他和他們一樣,推導不出來batchnorm_backward_alt就放棄跳過,死磕,不死磕心裡永遠有個結。
2. Dropout 层的梯度计算
Dropout 前向传播
在训练时,Dropout 随机将部分神经元的输出置为 0,以减少过拟合:
- 生成掩码(mask),通常是一个与输入相同形状的矩阵,元素是 0 或 1:其中 $p$ 是保留概率。
- 应用掩码:
在测试时,通常不使用 Dropout,但会将输出按比例缩放 $y = x \cdot p$。
Dropout 反向传播
Dropout 的反向传播非常简单,因为它的梯度只需考虑 mask 的影响:
chain rule 多元複合函數求導法則
我们需要计算 $ z = f(x, y) $ 对 $ t $ 的偏导数,其中 $ f(x, y) = \frac{x - y}{y} $,并且 $ x = g(t) = t^2 $,$ y = h(t) = 2t $。
z = f(x, y)其實就=t/2 - 1,導數是1/2,這個例子對理解BN的梯度computational graph非常有幫助。
因為上面的 $Y = \gamma \cdot \frac{x_i - \mu}{\sigma} + \beta$ 就可以改寫成$L = f(\Phi, \Psi, \Omega), \Phi = a(x) = x, \Psi = b(x) = mean, \Omega = c(x) = std, f(\Phi, \Psi, \Omega) = \frac{\Phi - \Psi}\Omega$。
步骤 1:应用链式法则
根据链式法则:
首先,我们需要计算各个部分的偏导数和导数。
步骤 2:计算 $ f(x, y) = \frac{x - y}{y} $ 对 $ x $ 和 $ y $ 的偏导数
对 $ x $ 的偏导数:
对 $ x $ 求偏导数,视 $ y $ 为常数:
对 $ y $ 的偏导数:
可以用商法则(商的求导法则)来求导:
所以我们得到了:
步骤 3:计算 $ x = g(t) = t^2 $ 和 $ y = h(t) = 2t $ 对 $ t $ 的导数
$ x = t^2 $ 对 $ t $ 的导数:
$ y = 2t $ 对 $ t $ 的导数:
步骤 4:将各部分代入链式法则
将以上结果代入链式法则公式中:
代入具体的表达式:
将 $ x = t^2 $ 和 $ y = 2t $ 代入:
简化:
最终答案:
总结:
通过链式法则,我们计算得到了 $ z $ 对 $ t $ 的偏导数为 $ \frac{1}{2} $。
一個變量的導數和他本身維度通常一致
1. 标量对矩阵的导数
如果标量 $f$ 是矩阵 $\mathbf{X}$ 的函数,那么 $\frac{\partial f}{\partial \mathbf{X}}$ 的结果是一个与 $\mathbf{X}$ 维度相同的矩阵。例如:
其中 $\mathbf{X}$ 是 $n \times m$ 的矩阵,$\mathbf{a}$ 是 $n$-维向量,$\mathbf{b}$ 是 $m$-维向量。那么:
它与 $\mathbf{X}$ 的维度 $n \times m$ 相同。
2. 矩阵对标量的导数
如果矩阵 $\mathbf{X}$ 是标量 $f$ 的导函数(例如梯度),我们也可以得到一个与 $\mathbf{X}$ 维度相同的矩阵:
3. 矩阵对矩阵的导数
如果需要计算一个矩阵对另一个矩阵的导数,例如 $\frac{\partial \mathbf{A}}{\partial \mathbf{B}}$,那么结果通常是一个四维张量。这是因为:
如果 $\mathbf{A}$ 和 $\mathbf{B}$ 的维度分别是 $n \times m$ 和 $p \times q$,则结果是一个 $n \times m \times p \times q$ 的张量。
例如,对于 $\mathbf{A} = \mathbf{B}^2$,结果张量会考虑所有元素的依赖关系。
总结
- 标量对矩阵的导数,结果与矩阵维度相同。
- 矩阵对标量的导数,结果也与矩阵维度相同。
- 矩阵对矩阵的导数,结果通常是一个四维张量,与原矩阵的维度不同。
Notes
https://cs231n.stanford.edu/slides/2017/
https://cs231n.stanford.edu/slides/2024/ 今年的也大差不差,lecture6都是講Batch Normalization,甚至很多圖都一樣。
https://cs231n.github.io notes在這(其實用slides裡的圖片這篇筆記的圖片會很小,但懶得挨個扒,截圖堆成超大圖片屎山了。)
2018,2019 年也都是 Justin Johnson 和 Serena Yeung,slides 完全沒變,不知為啥 Justin Johnson 從 2016 上這門課四年不說, 2019 年又去 Michigan 講了一遍;2020,2021 年是 Ranjay Krishna, Danfei Xu ,2021年有了 Self-Supervised Learning Lecture 13,而且雖然 2019 年就講了 self-attention 和 transformer,2021 年才加入了 assignment;2022 年是 Jiajun Wu, Ruohan Gao;2023 年是 Yunzhu Li, Ruohan Gao,Google Deepmind 去做了 Guest Lecture,講了 VAE 和 2022 年我上班時火遍地球的 Diffusion Models;2024 年是 Ehsan Adeli, Zane Durante,內容幾乎沒變。
Lecture 1
From PASCAL Visual Object Challenge(20 object categories) to ImageNet (Deng, Dong, Socher, Li, Li, & Fei-Fei 2009). 李飞飞他们花了3年, 从互联网上下billions of images,然后用WorldNet这个词典把图像组织起来(which has tens of thousands of classes),然后用Amazon Mechanical Turk平台排序、清洗、标注图像。然后开放了Large Scale Visual Recognition Challenge,“输入是image,输出是label,用前五个labels是否正确来作为指标”作为benchmark评价进展。2012年CNN(from 1998 LeCun to recognize handwriting digits and addresses for the post office)把error rate从26降到了16,从此一发不可收。
WordNet是一个由普林斯顿大学认识科学实验室在心理学教授乔治·A·米勒的指导下建立和维护的英语字典。开发工作从1985年开始,从此以后该项目接受了超过300万美元的资助(主要来源于对机器翻译有兴趣的政府机构)。
WordNet根据词条的意义将它们分组,每一个具有相同意义的字条组称为一个synset(同义词集合)。WordNet为每一个synset提供了简短,概要的定义,并记录不同synset之间的语义关系。
http://wordnetweb.princeton.edu/perl/webwn

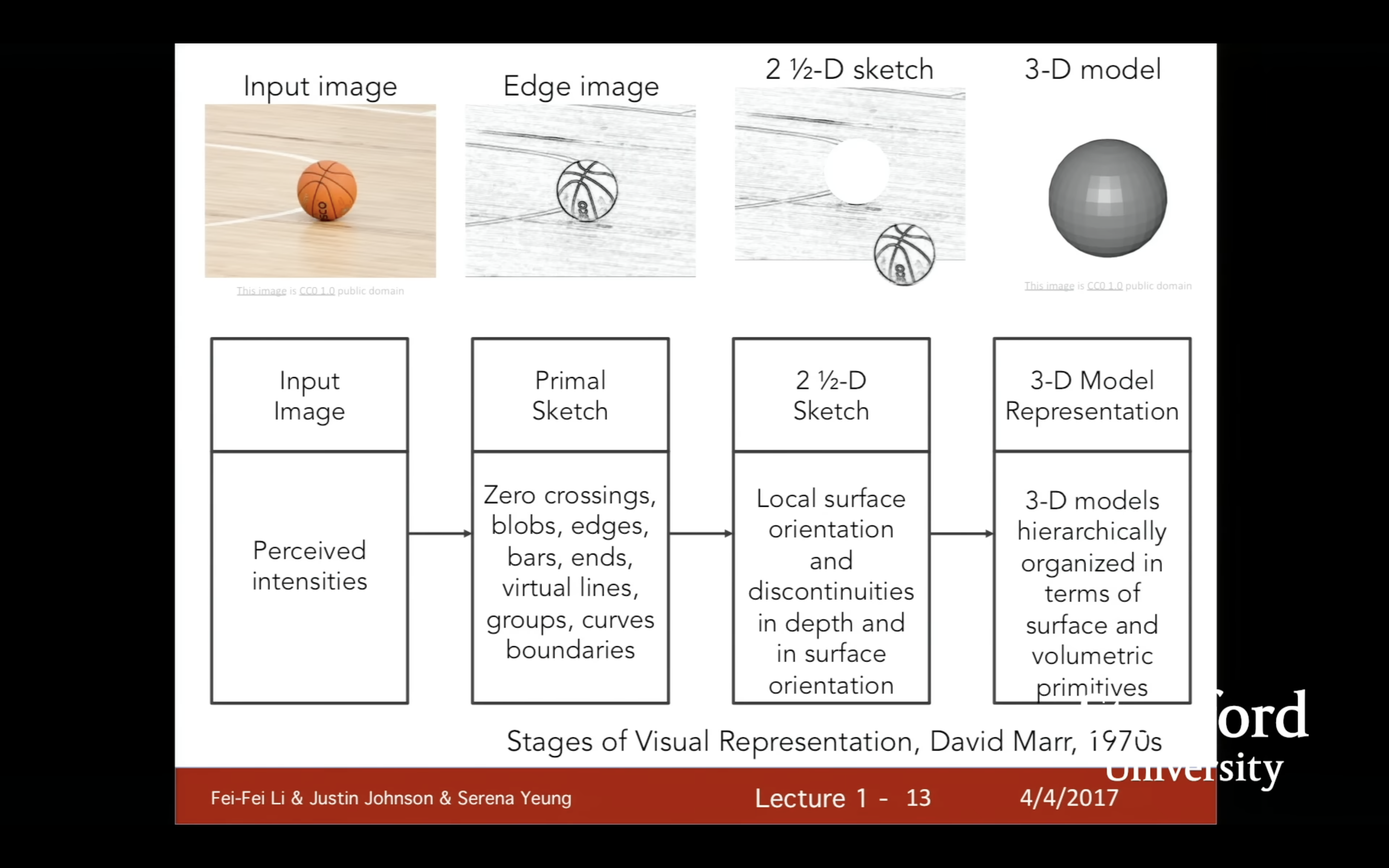
The primary focus of this class is Image Classification (A core task in Computer Vision ), the setup is that your algorithm looks at an image, and then picks from among some fixed set of categories to classify that image. This might seem like somewhat of restrictive or artificial setup, but it’s actually quite general. This problem can be applied in many different settings both in industry and academia and many different places. But in this course we are also gonna talk about several other visual recognition problems that build upon many of the tools that we develop for the purpose of image classification, such as, object detection and image captioning.
这也是我后来一直存在的疑问,当时没仔细看错过了这个关键问题。AI的最终目标比如图像分类这个任务从来不是能识别一切图像,因为视觉信息这个二维量本身就是局限的,通用AI(AGI)的目标是能做出人类所有智能行为的AI,所以超越人类水平已经足够了。
这个技术的价值是能应用到所有场景里,比如在饭店判断菜品的任务里,能超过人的准确率就已经可以接受了。
回顾在商汤做的visual grounding任务,输入“这个垃圾桶是满的”,视觉定位模型找到图像中的垃圾桶并输出“是”“否”满。其实完全能分割成目标检测+图像分类任务,只是因为对这些基础技术太不熟练导致思路模糊,只能跟着团队用OFA人云亦云亦步亦趋。随便搭一个两步的模型对从事这项工作的人来说应该是最基础的事,基础不牢地动山摇。(不过当时团队是侧重于做一个能快速适应新场景的模型,经过几十张甚至0张图片的训练就能检测新任务比如“电动车有没有超载”,但一样也该入职时迅速搭一个两步模型上手任务。)
(关于Justin Johnson这句话的语法,from among的among强调范围,是对的;some set的some表示不确定,set是对的,sets大概也可以)
另外,AI的飞速发展一直让过去的我焦虑,这种焦虑让我不愿意学习当前的sota技术,因为未来某一天就突然会被革新。可现在回头看,雖然沒有新的課堂錄像,但通過課程官網可以看出stanford的cs231n内容几乎从未改变,这足以说明这些老玩意还是新积木的基石。
Lecture 2
Numpy efficiently implements vectorized operations. It’s should be practiced a lot in assignment 1.
就识别猫这个问题来说,通过找到所有edges然后根据猫的特征逐一匹配(耳朵眼睛尾巴,大致间距和位置)大概也可以做到,而且这样的代码完全可解释。而现在neural nets的data driven,根本不可能讲清楚哪个部分识别了哪个特征,能把握的只有梯度变化规律。
knn也是data-driven的,只不过不从training data里获得知识,只是简单记住train set,来一个新数据就跟所有train set数据比较,跟哪个类别的某k个图最相似那就属于哪个类别。如何计算两个图(向量)的距离(Distance Metric)四年前已经总结过了,可以用L1曼哈顿也可以用L2欧式,对于新问题用什么距离试试哪个好就行了。训练O(1),推理O(N),正好反了。
只要记住KNN的full form——K Nearest Neighbors就能想起来这个dumb算法了。
metric不是metrix,metric is a system for measuring something是指标的意思;metrix才是矩阵。
模型在train set上训练完后,在validation set上找最优hyperparameters(不靠训练得到的都算,包括距离计算L1还是L2),最后临论文deadline,只在test set上跑一次only once,得到的数就是最终写在报告、论文里的数据,以保证没有作弊。严格分离验证集和测试集对确保做研究没有不诚实、不公平很重要。
| validation set for tuning hyperparameters | |
|---|---|
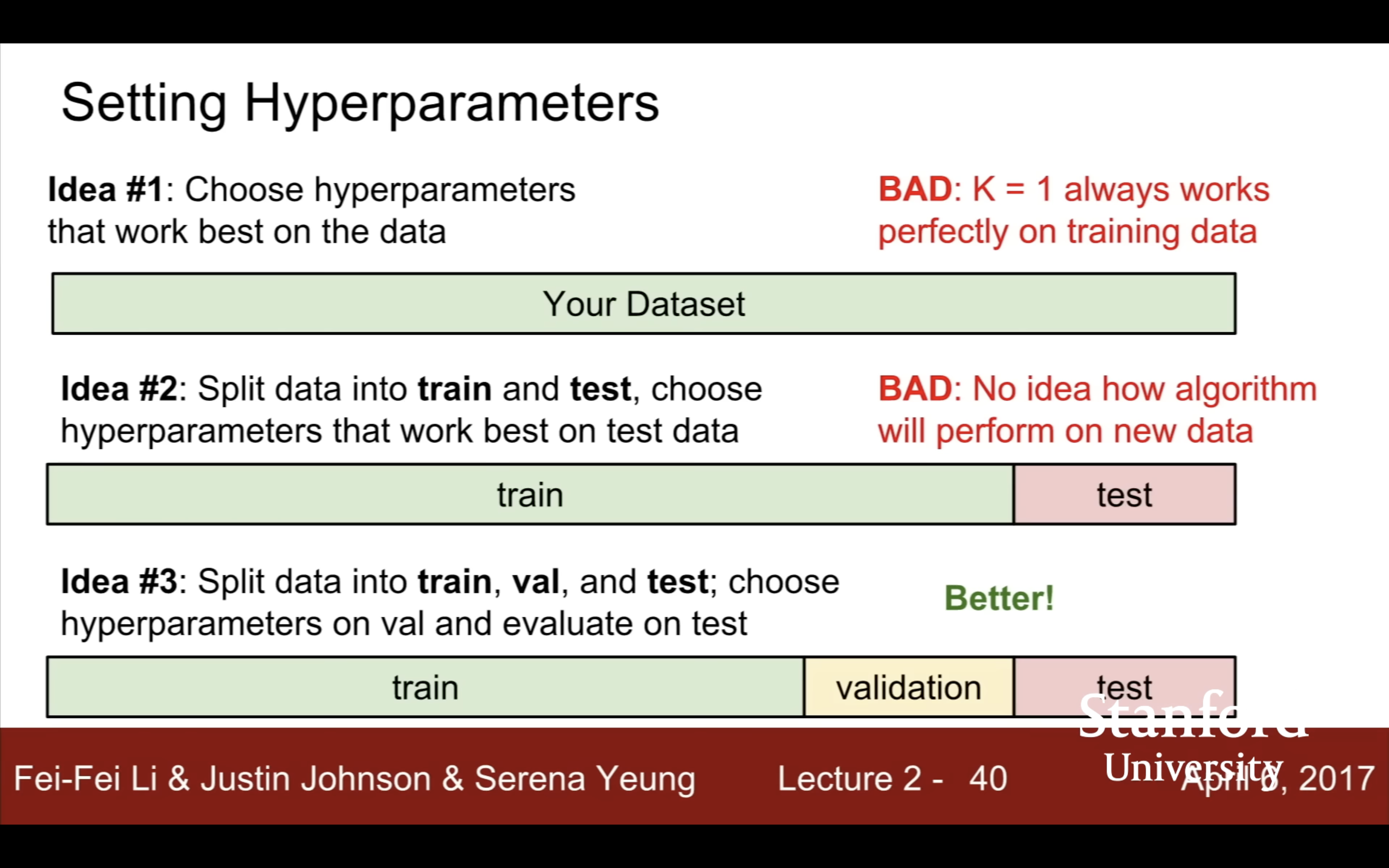 |
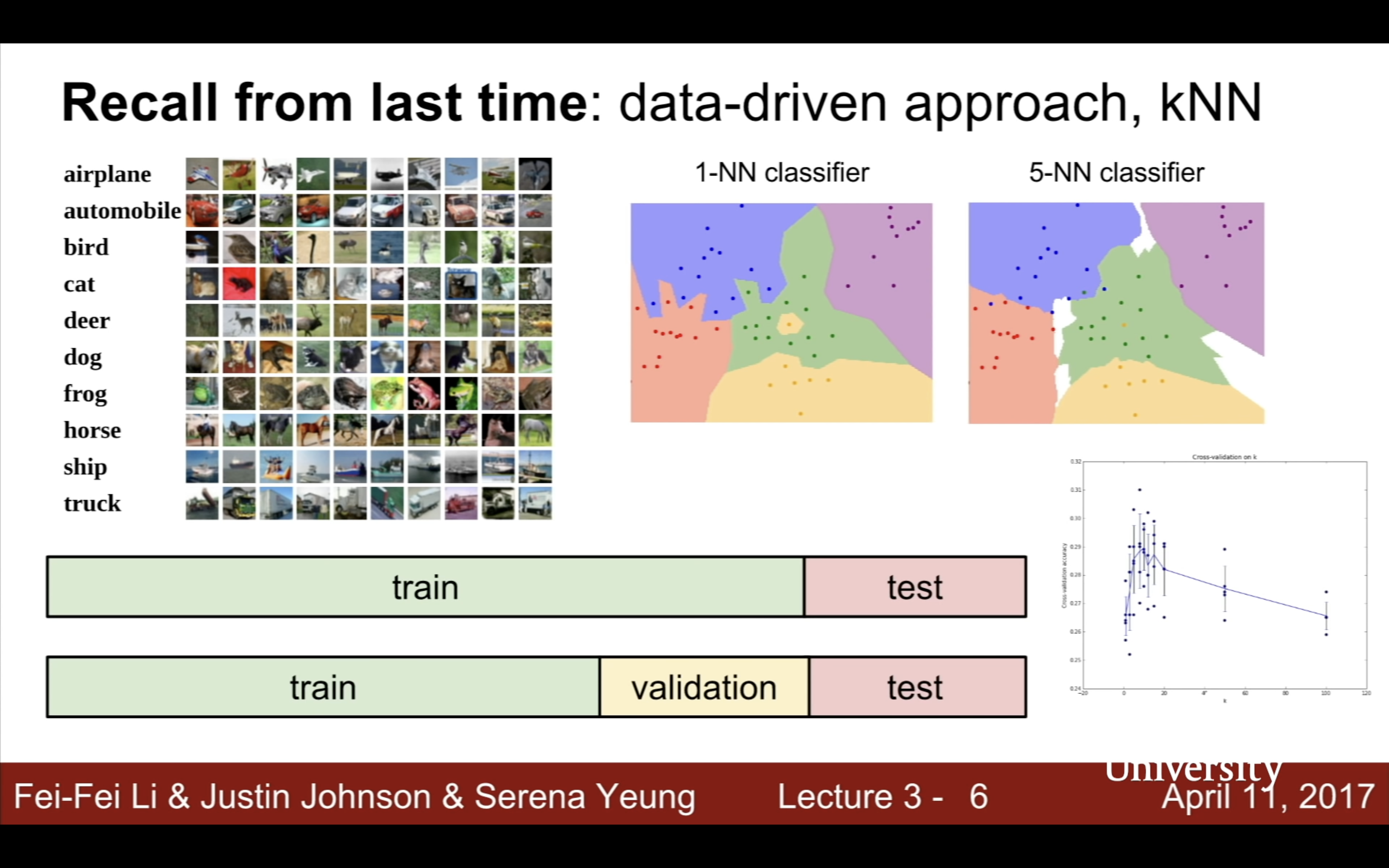 |
另外idea4是交叉验证,神经网络实验的验证集validation set一般不用cross validation,在不同分割的训练集上训练好几遍开销太大了,只适用于较小的数据集。

linear classification是最簡單的parametric model(即上面的f(x,W)也有時weights/paramters會寫成theta θ而不是W),用Xtrain训练出W参数,inference过程就可以抛弃训练数据只用x和W计算结果。
最简单的x和W组合方式就是二者相乘。
其中對bias的簡單理解是,数据集里的猫比狗多,那猫类别的bias值可能就比狗高。可以通过增加一个常数项1特征,把b算作W的一部分。
模型做的通常是在给定幾個类别里打分的工作,而不是凭空产生一个相关类别,人脑大概也是这么工作的——看到一张猫的图片,在语言系统的无数个词条里关联到“猫”。
在很多模型裡linear classification就作為最後一層,承擔把所有的計算匯總到一起給上面10個類別打分的工作。
可以把linear classification的Wx这个計算过程看成是template matching,這在我之前的筆記也寫過一次,weights的每一行可以看作是一個被strech成一維的模板,圖片跟模板越像的話,在這一類的分數就會越高。
這是因為這兩個vector的點積就是點積相似度,點積越大可以認為就越相似,因為圖片的每個像素都是個xyz-axis都在0~255內的向量,所以可以把這個點積相似度放在r=255的球裡來想,或許有幫助。


在neural network等其他複雜模型裡,不會只限制模型每個類別只學一個模板,可能因此才變得更準確。
这种可视化方式可以学来,用在神经网络里可视化一下参数。不过我之前也可視化過比如capsule,能看出參數對應圖像的一些特徵,但不像linear这么明显。
| 站在比數據高一點兒維度的角度看問題 | 單純linear decision boundaries顯然解決不了的問題 |
|---|---|
 |
 |
之後的內容可以理解成:
- Loss function (quantifying what it means to have a “good” W)
- Optimization (start with random W and find a W that minimizes the loss)
- ConvNets! (tweak the functional form of f)
Problems:
- KNN:(never used)
- Very slow at test time.
- Distance metrics on pixels are not informative.
- Curse of dimensionality.

Lecture 3

想一些相關問題有助於理解:
- 選margin為1還是其他數字無所謂,只是一個arbitrary choice;
- 車的分數稍微改變一下不影響loss仍然為0;
- 就像hinge曲線一樣,loss最小值為1,最大值為infinity;
- 讓W為全0,即s≈0,那麼loss應該是num of classes - 1,這個可以用於debug;
- 讓j可以=y_i的話,結果是loss-1,其實都一樣但是讓loss最小值為0而不是“1”比較make sense;
- 計算loss不用sum,用mean也沒區別,因為不關心loss絕對值;
- 如果用上式loss的平方,可以代表我們更不能容忍大的錯誤,因為錯誤較大的類別會直接指數倍放大;
- 如果loss=0,這時的W是唯一的嗎?當然不是,2W的loss也是0。
def L_i_vectorized(x, y, W) : |
相比想矩陣,用一條數據vector的例子分析example code比較簡單。
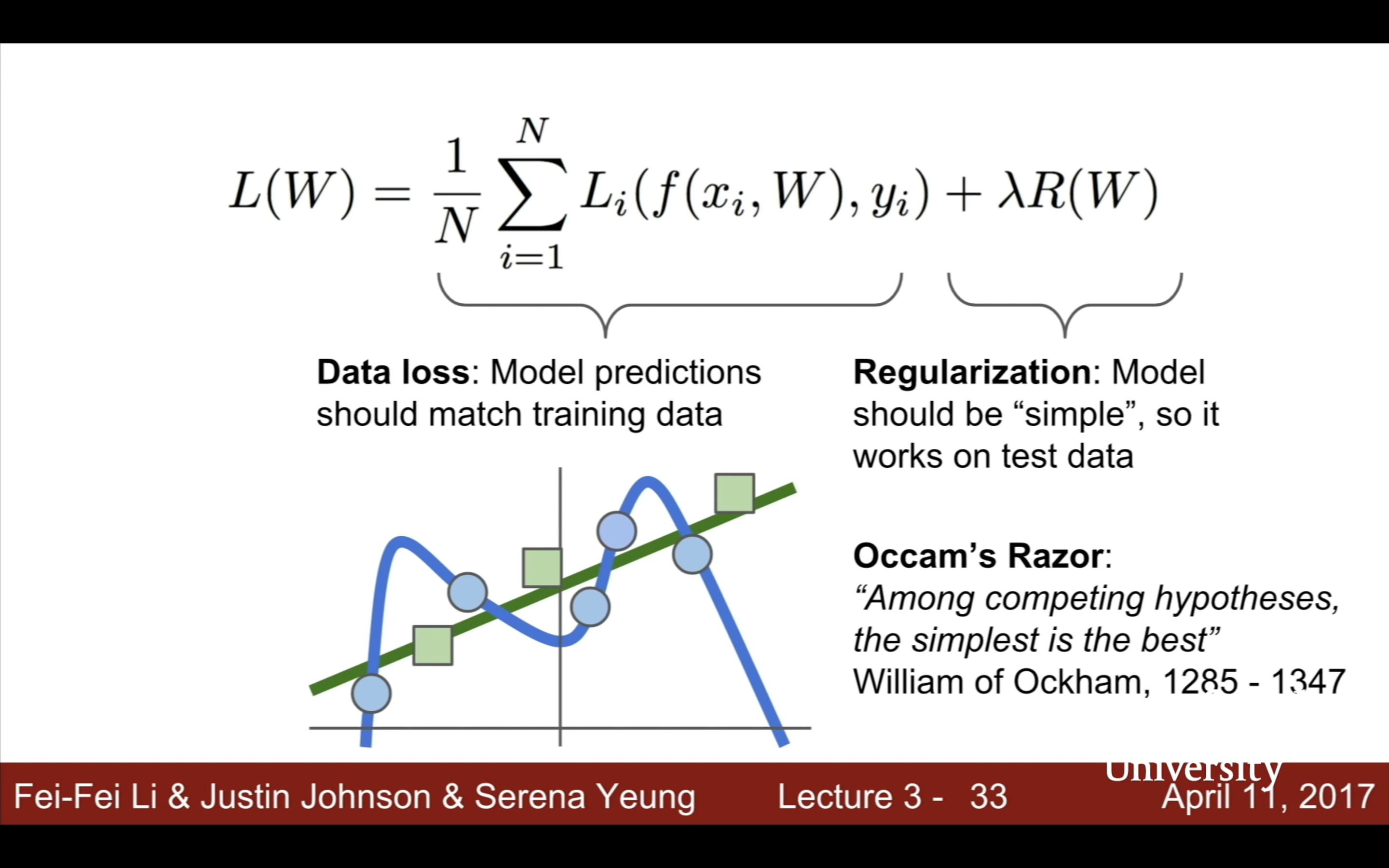
| Occam’s Razor: “Among competing hypotheses, the simplest is the best” William of Ockham, 1285 - 1347 | 發現regularization是“W”的函數,是讓W越簡單越好,比如讓高次冪特徵係數為0 |
|---|---|
 |
 |
之前學cs231n就是卡在batch normalization附近了,這一曠就是四年。總之還是沒理解清防止過擬合加的正則項到底是個什麼。需要找點最簡單的例子,具體分析。
 |
 |
想一些相關問題有助於理解:
- min:-log(1)=0 max:-log(0)=infinity,但這兩個值都是取不到的,因為如果softmax函數=1,錯誤類別都需要是負無窮才能e^sj為0,如果softmax=0,正確類別分數需要是負無窮e^sy才能為0;
- 如果W=0,s全≈0,L_i就=-log(1/C(num of classes))=log(C);這個也可以用來debug,跟上面SVM一樣!
- 對比一下再來想問題3:
 |
 |
如果是右圖這種情況,修改一點已經分類正確的分數,svm loss仍然是0不會變,而softmax會改變,因為svm的目標是只要正確分類的score跟錯誤分類差距大過margin就可以了,而softmax會盡可能地把錯誤分數拉向-inf,把正確分數拉向inf。
- svm和softmax都只是為了最優化f(x)=Wx+b的損失函數而已,他們的函數形狀不重要,f(x)=Wx+B仍是線性函數
關於optimizer他的解釋很有意思,解析解analytic solution像是你在山頂(高度就是loss值)magically teleport到了最低點,但當prediction function f,loss function包括regularizer都很複雜就只能尋求數值解(iterative methods that start some solution and gradually imporve by time,梯度下降,即求導按負導數方向找低點,高中數學,pretty easy actually)。
- Strategy #1: A first very bad idea solution: Random search
Strategy #2: Follow the slope

一種計算gradient的想法是——,但是這方法太蠢太慢了,Numerical gradient: approximate :(, slow :(, easy to write :)

Analytic gradient: exact :), fast :), error-prone :(,直接用微積分得到dW迭代loss

In practice: Always use analytic gradient, but check implementation with numerical gradient. This is called a gradient check.(finding derivative is error-prone求導是容易出錯的)
chatgpt給的一個計算梯度的例子
示例函数
假设我们有一个二维函数:
这个函数是一个标准的二次函数,描述的是一个圆形等高线的抛物面。我们的目标是计算其梯度,并理解梯度的含义。
1. 计算梯度
首先,梯度是指函数在不同方向上变化的速率,它由偏导数组成。在二维情况下,梯度可以写成一个向量:
求偏导数:
计算 $f(x, y) = x^2 + y^2$ 对 $x$ 和 $y$ 的偏导数:
对 $x$ 的偏导数:
对 $y$ 的偏导数:
因此,梯度 $\nabla f(x, y)$ 为:
2. 梯度的意义
在几何上,梯度是函数在该点变化最快的方向。具体来说,梯度的方向就是函数值增长最快的方向,而梯度的负方向(即 $-\nabla f$)则是函数值下降最快的方向。
示例:在点 $(1, 1)$ 处的梯度
假设我们在点 $(1, 1)$ 计算梯度:
这表明,在点 $(1, 1)$ 处,函数 $f(x, y)$ 增长最快的方向是向量 $(2, 2)$ 的方向。这个方向对应于45度方向,即沿着 $x$ 轴和 $y$ 轴方向各增加1的方向。
3. 如何找到梯度最大的方向
梯度本身就表示函数变化最快的方向。它的方向指向函数值增长最快的方向,而它的大小(即梯度的模)则表示变化的速率。
在我们的例子中,点 $(1, 1)$ 的梯度是 $(2, 2)$,它的模为:
总结:
- 在任意点 $(x, y)$ 处,函数 $f(x, y) = x^2 + y^2$ 增长最快的方向是沿着梯度方向 $(2x, 2y)$。
- 梯度的大小表示函数在该方向上增长的速率。
- 如果我们想沿着函数值降低的方向移动,那么应当沿着梯度的负方向移动。
所以gradient descent的代碼也很簡單:# **Vanilla Gradient Descent**
while True:
weights_grad = evaluate_gradient(loss_fun, data, weights)
weights += - step_size * weights_grad # perform parameter update
其中loss_fun就可以想像成上面的f(x,y,z)=x^2+y^2+z^2,data就是x,y,weights就是z。
learning rate(step size)是最先要確定的超參數,model size和regularization strength都是其次的。
fancier update rules than gradient descent:
momentum, adam,就是不同的利用梯度信息的方式。
比如稍微改進vanilla為stochastic(SGD隨機梯度下降是隨機選一個,這裡是變種Mini-batch Gradient Descent):

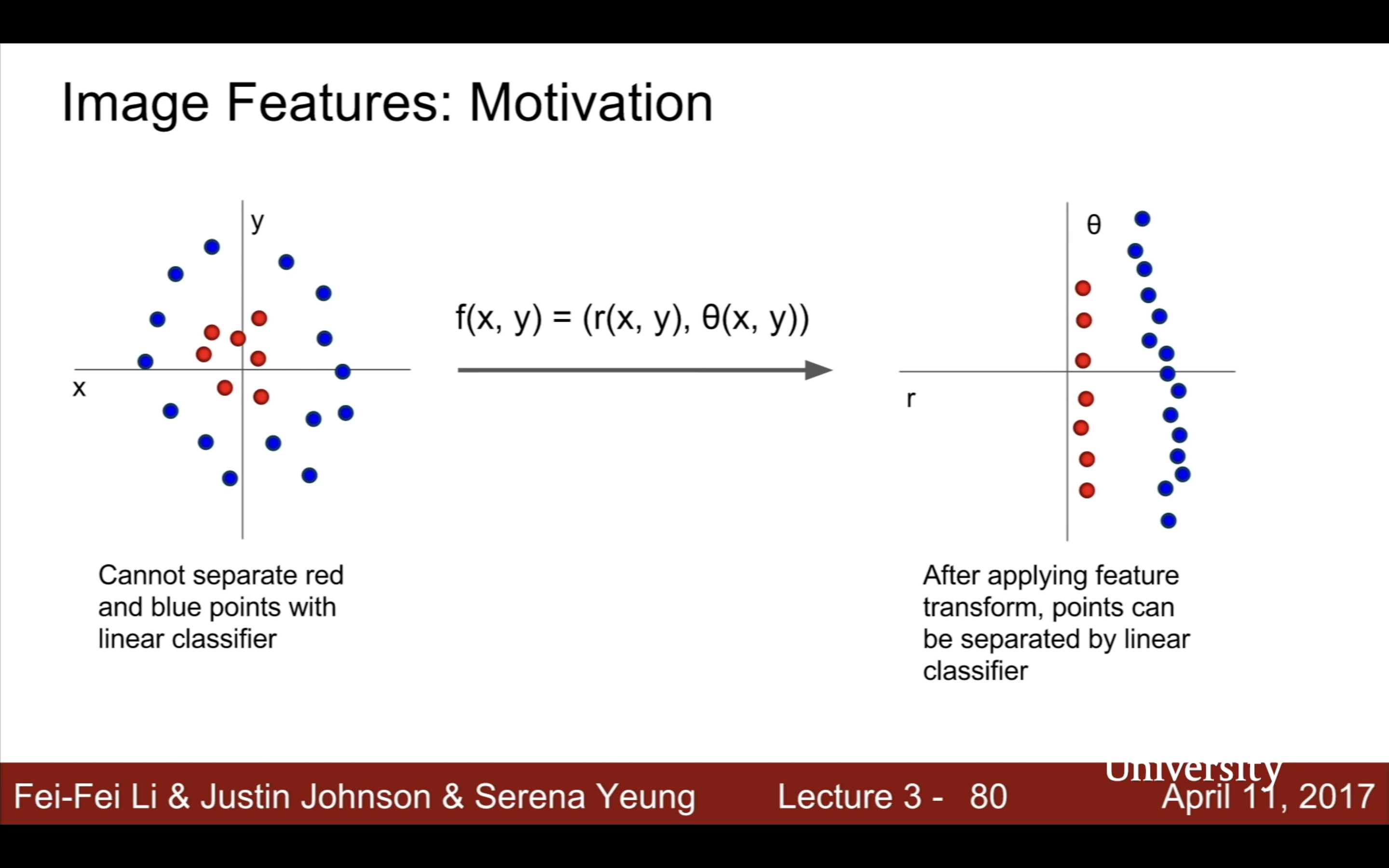
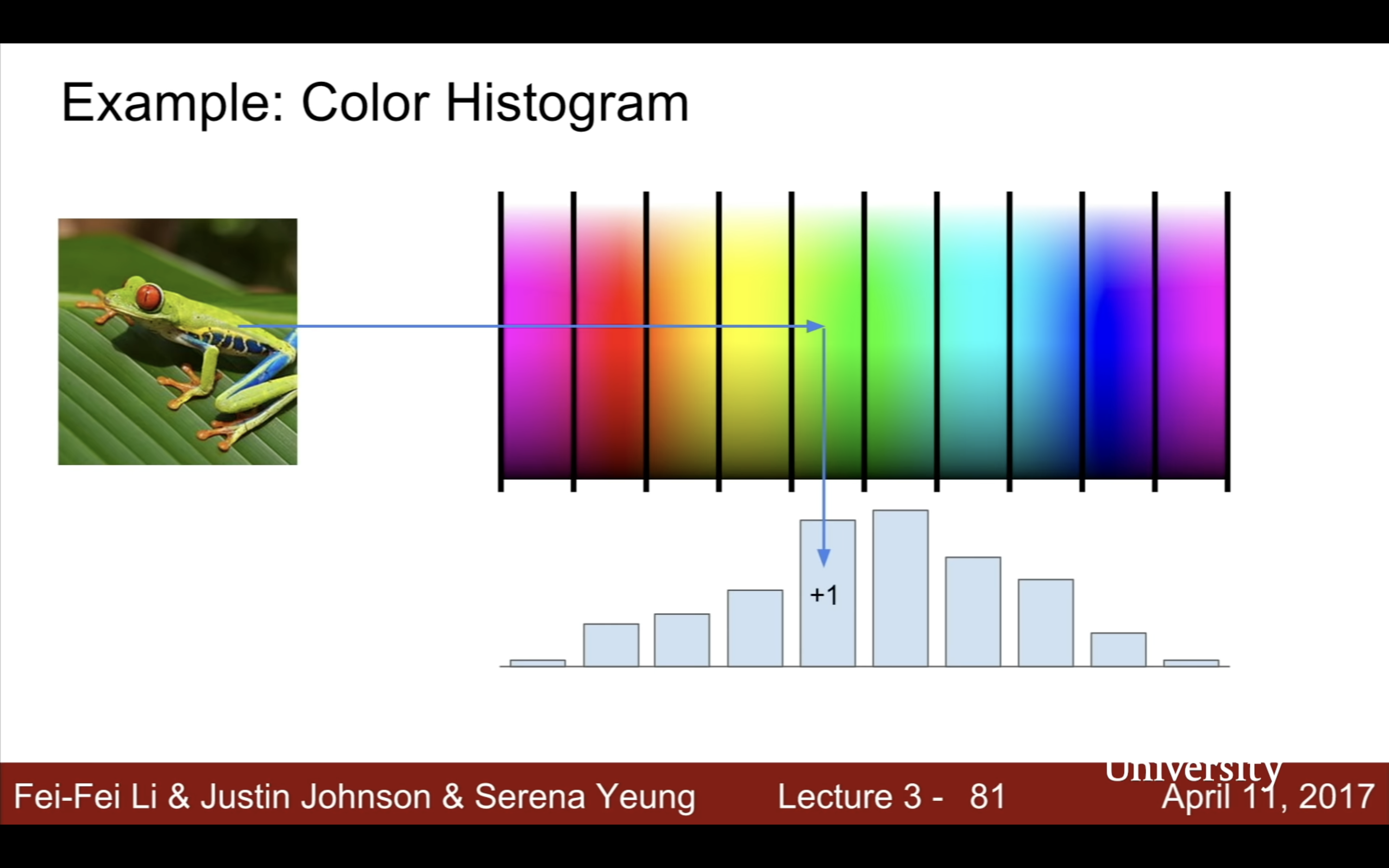
| features | color histogram | edge histogram | like codebook(OFA啥的也有這個概念來著?) | 現在跟以前先提取特徵的兩步法也沒什麼區別,包括cnn,包括transformer,只是變成隱性地提取這些特徵,做成end to end端到端的黑箱 |
|---|---|---|---|---|
 |
 |
 |
 |
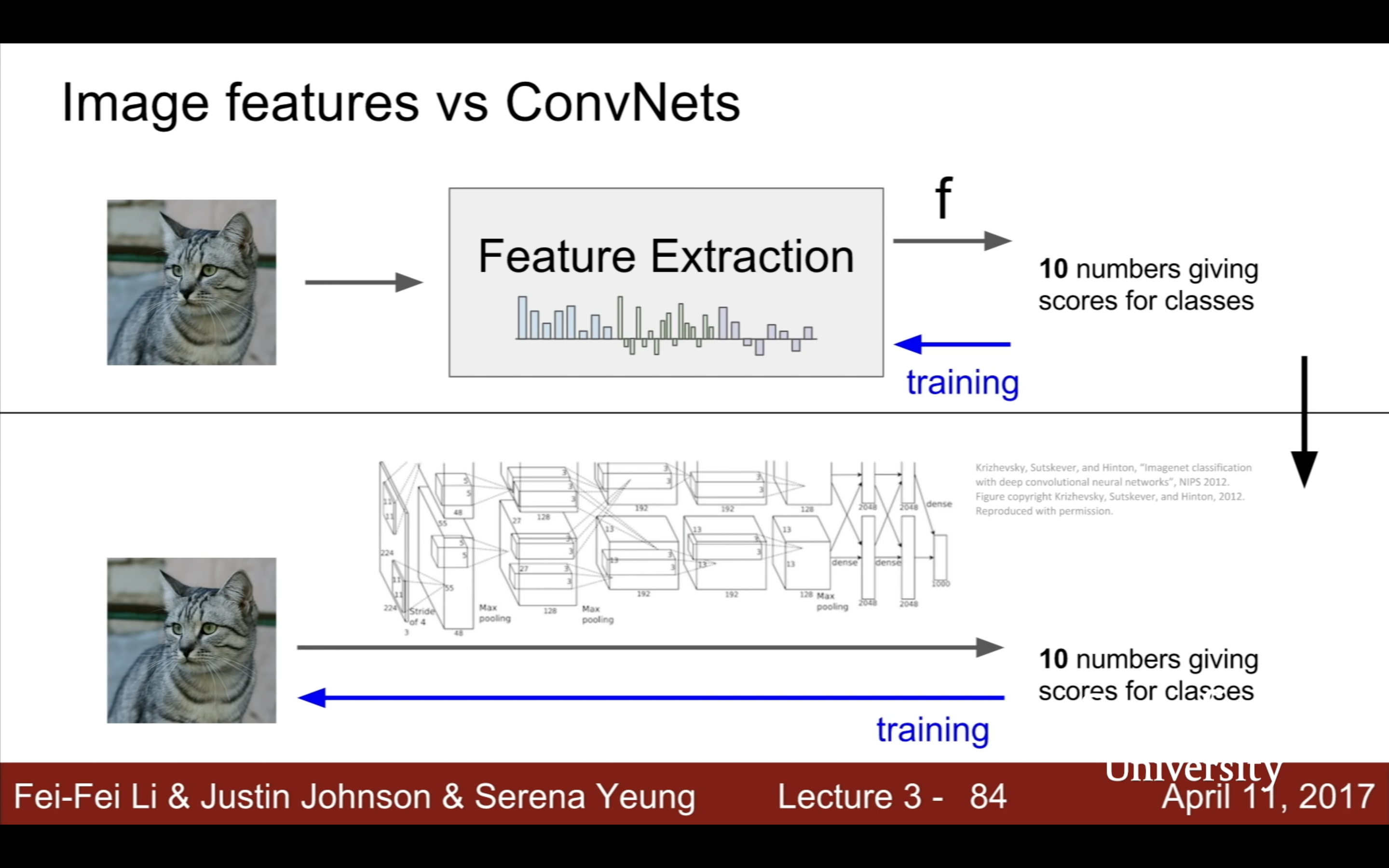 |
Lecture 4 計算圖(local gradient and chain rule)
| computational graph chain rule | 每個node只需要關注它周圍的nodes |
|---|---|
 |
 |
 |
 |
| 把幾個基本二元運算合成一個計算模塊,比如sigmoid,和它的導數 | 這裡算導數用的不是x,是f(x),由此可知backprop時node的forward pass的前後值都可能用到 |
|---|---|
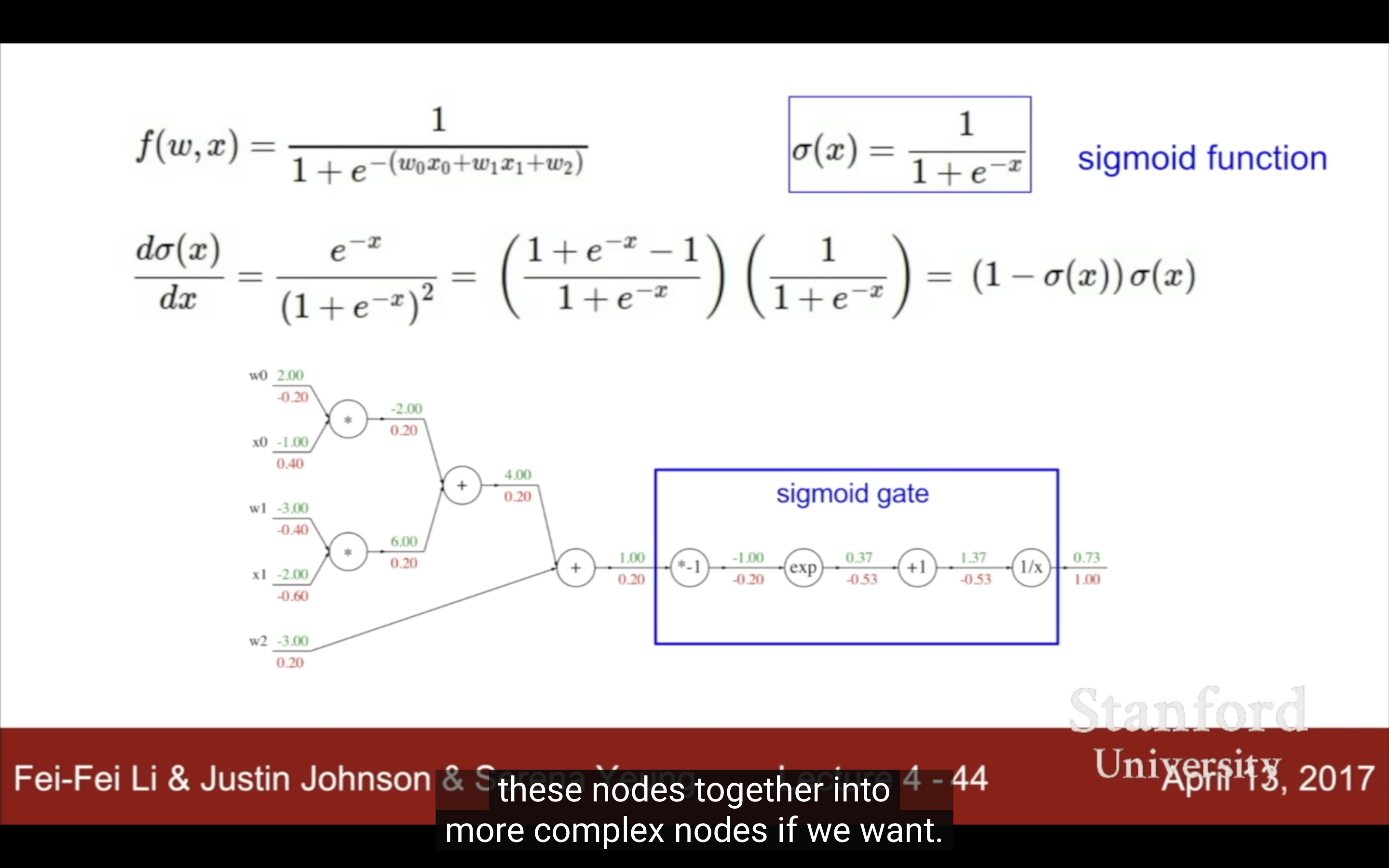 |
 |
任何時候比如做assignments時,如果求梯度遇到困難,畫一個計算圖用chain rule就都可以迎刃而解。
| patterns | pattern |
|---|---|
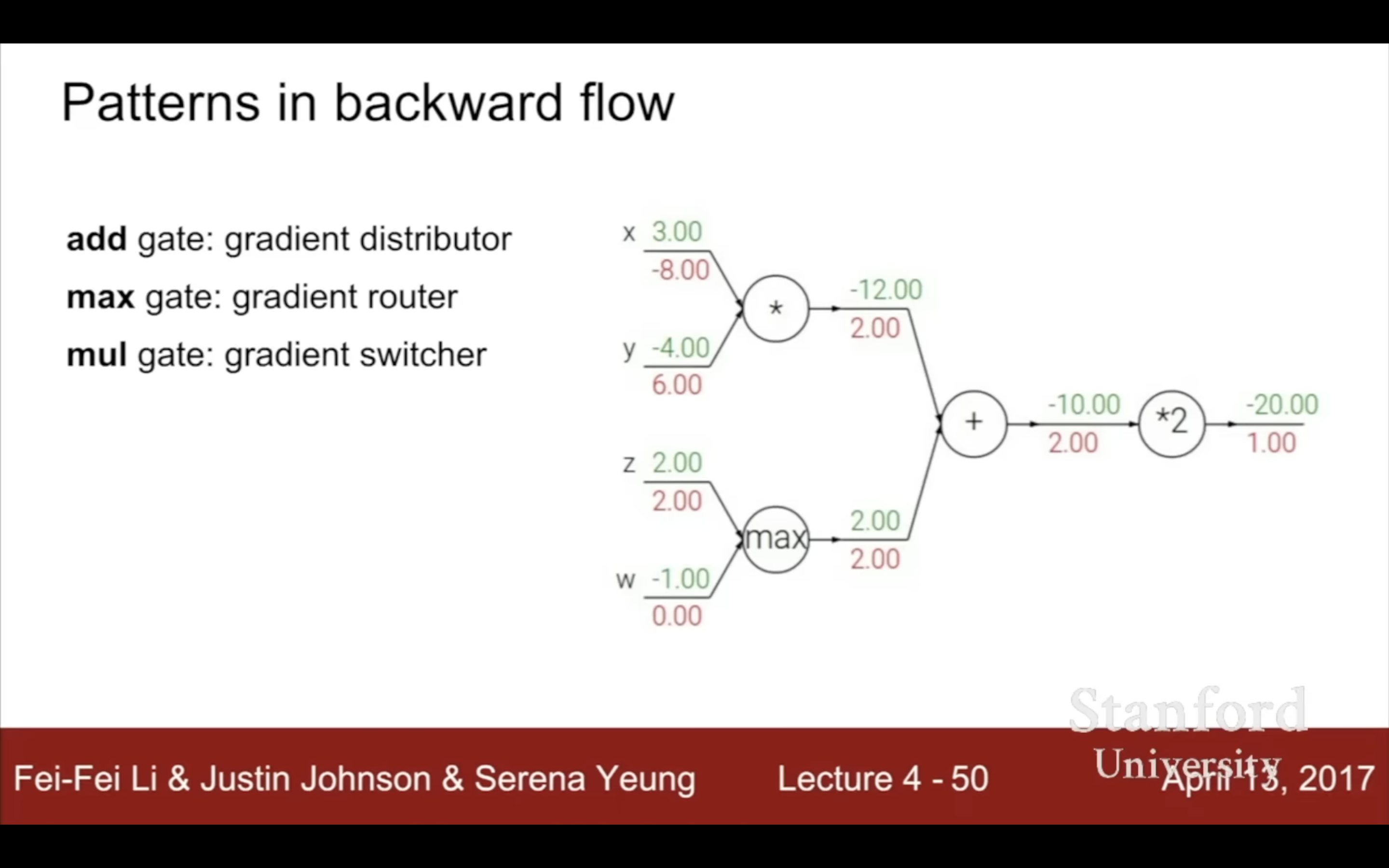 |
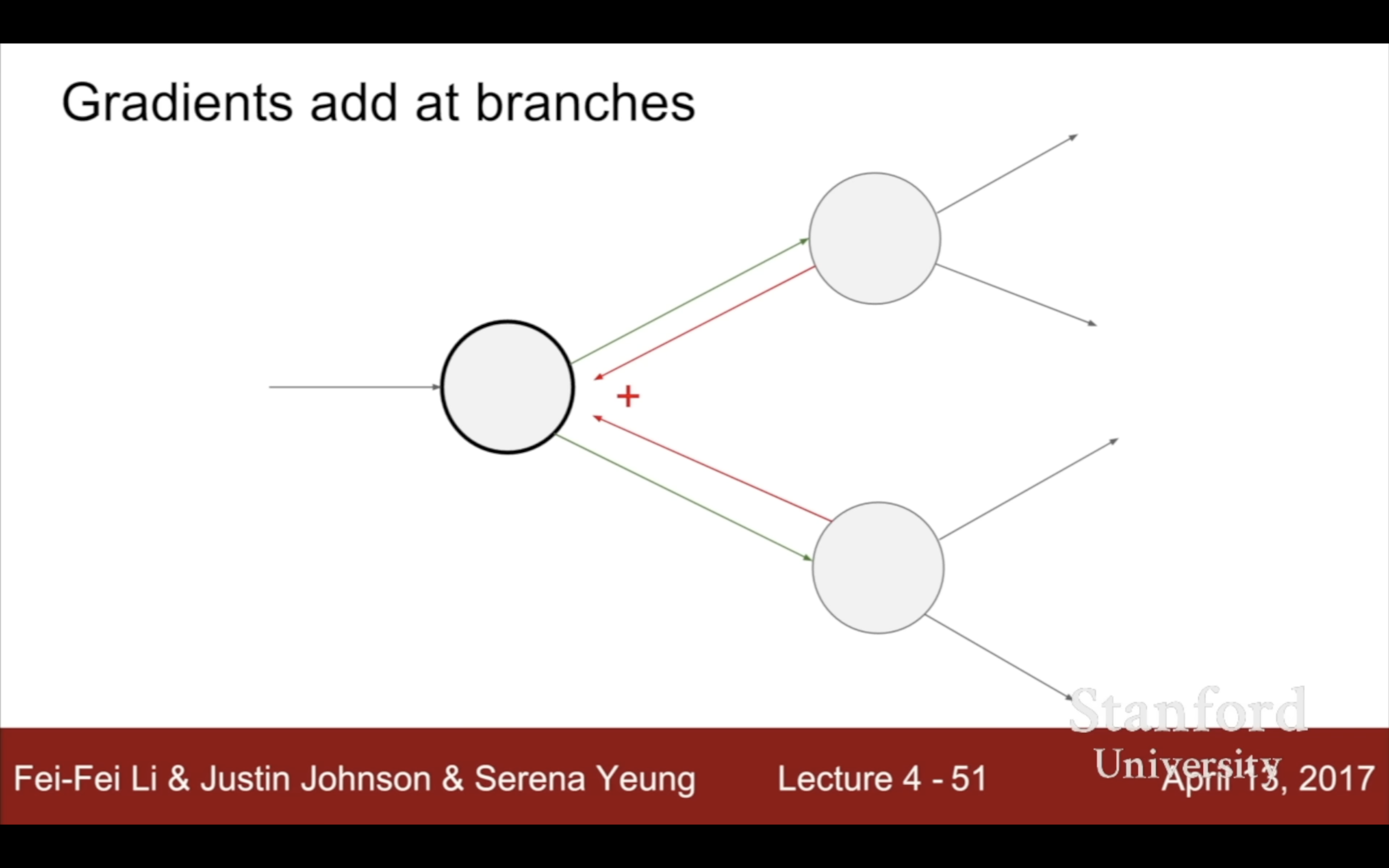 |
$\frac{df}{dx} = \sum_i \frac{df}{dq_i} \cdot \frac{dq_i}{dx}.$
懶得畫圖了,如果x給多個q當了自變量,多個q又給同一個f當了自變量,那就得把導數加起來,隨便想個computational graph的例子就不抽象了。
Jacobian矩陣很簡單,就是每個輸出對應每個輸入的偏導——
Jacobian 矩阵计算示例
Jacobian 矩阵在多元函数中用于描述一个向量值函数的偏导数。假设我们有一个向量值函数 $ \mathbf{F}(\mathbf{x}) $,其中 $ \mathbf{F} : \mathbb{R}^n \to \mathbb{R}^m $,输入向量 $ \mathbf{x} \in \mathbb{R}^n $,输出向量 $ \mathbf{F}(\mathbf{x}) \in \mathbb{R}^m $。
对于每一个 $ x_i $ 和 $ F_j $,Jacobian 矩阵的元素是 $ \frac{\partial F_j}{\partial x_i} $。整个矩阵的形式是:
示例
假设我们有函数(這裡的x和y當然可以改成x1和x2):
我们希望计算 $ F(x, y) = \begin{bmatrix} F_1(x, y) \\ F_2(x, y) \end{bmatrix} $ 的 Jacobian 矩阵。
第一步:计算偏导数
对 $ F_1(x, y) = x^2 + y^2 $:
- $ \frac{\partial F_1}{\partial x} = 2x $
- $ \frac{\partial F_1}{\partial y} = 2y $
对 $ F_2(x, y) = e^x + \sin(y) $:
- $ \frac{\partial F_2}{\partial x} = e^x $
- $ \frac{\partial F_2}{\partial y} = \cos(y) $
第二步:构造 Jacobian 矩阵
将上述结果代入矩阵中:
第三步:在特定点的 Jacobian 矩阵
如果我们希望在特定点,比如 $ (x, y) = (1, 0) $ 处求得 Jacobian 矩阵,则代入此点的值:
结果
因此,函数 $ F(x, y) $ 在点 $ (1, 0) $ 处的 Jacobian 矩阵为:
这个矩阵描述了函数 $ F(x, y) $ 在点 $ (1, 0) $ 处的变化率和方向。
| because each element of your gradient is quntifying how much element is contributing/affecting your final output | 下面偽代碼的forward和backward | |
|---|---|---|
 |
 |
 |
關於這個1(indicator function):
这个符号 $1_{k=i}$ 表示一个指示函数(或称为指示符号),其作用是判断条件 $k = i$ 是否成立:
- 当 $k = i$ 时,$1_{k=i} = 1$
- 当 $k \neq i$ 时,$1_{k=i} = 0$
因此,如果写成 $1_{k=i} x_j$,则表示仅当 $k = i$ 时,值为 $x_j$;如果 $k \neq i$,则值为 0。
所以就可以簡單寫一下計算圖的rough pseudo code:class ComputationalGraph(object):
#...
def forward(inputs) :
# 1. [pass inputs to input gates...]
# 2. forward the computational graph:
for gate in self.graph.nodes_topologically_sorted():
gate.forward()
return loss # the final gate in the graph outputs the loss
def backward():
for gate in reversed(self.graph.nodes_topologically_sorted()):
gate.backward() # little piece of backprop (chain rule applied)
return inputs_gradients
class MultiplyGate(object):
def forward (x,y) :
z = x*y
self.x = x # must keep these around!
self.y = y
return z
def backward(dz):
dx = self.y * dz # [dz/dx * dL/dz]
dy = self.x * dz # [dz/dy * dL/dz]
return [dx, dy]
caffe layers的代碼在這節課之後就沒變過。比如下圖這個sigmoid_layer。
| topdiff是上游梯度 | 寫之前先畫computational graph |
|---|---|
 |
 |
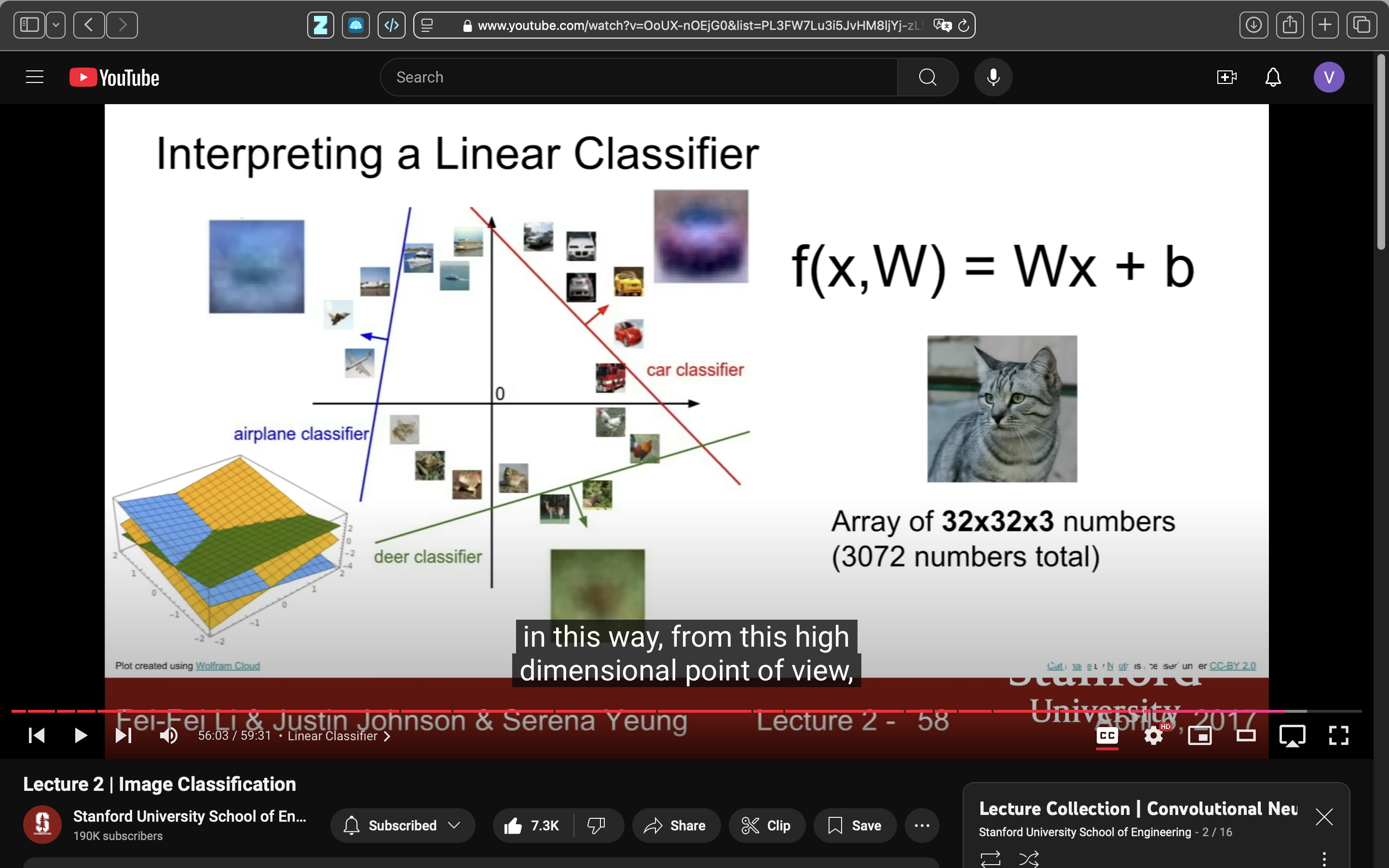
| if you just stack linear layers on top of each other, they’re just gonna collapse to a single linear function (w/o max here) | 這裡其實我一直有個疑問,如果X裡有x1 x1x2 x1x2x3這種高階特徵,那豈不是不再線性了?這個問題其實有點蠢,因為線性關係是指x1和f(x1)、x1x2和f(x1x2)、x1x2x3和f(x1x2x3)之間是線性/直線,而不是x1x2/x1x2x3跟f(x1) | 用之前template matching的觀點可以認為W1學到了更多templates(維度變大了),而W2是模板的weights,h是tempaltes得分,h之前會做non-linear(這裡是max),最後得分就是templates的weighted sum | 3層3-layer就是再套一次f = Wз max(0, W2 max(0, W1x)),代碼在下面 |
|---|---|---|---|
 |
 |
 |
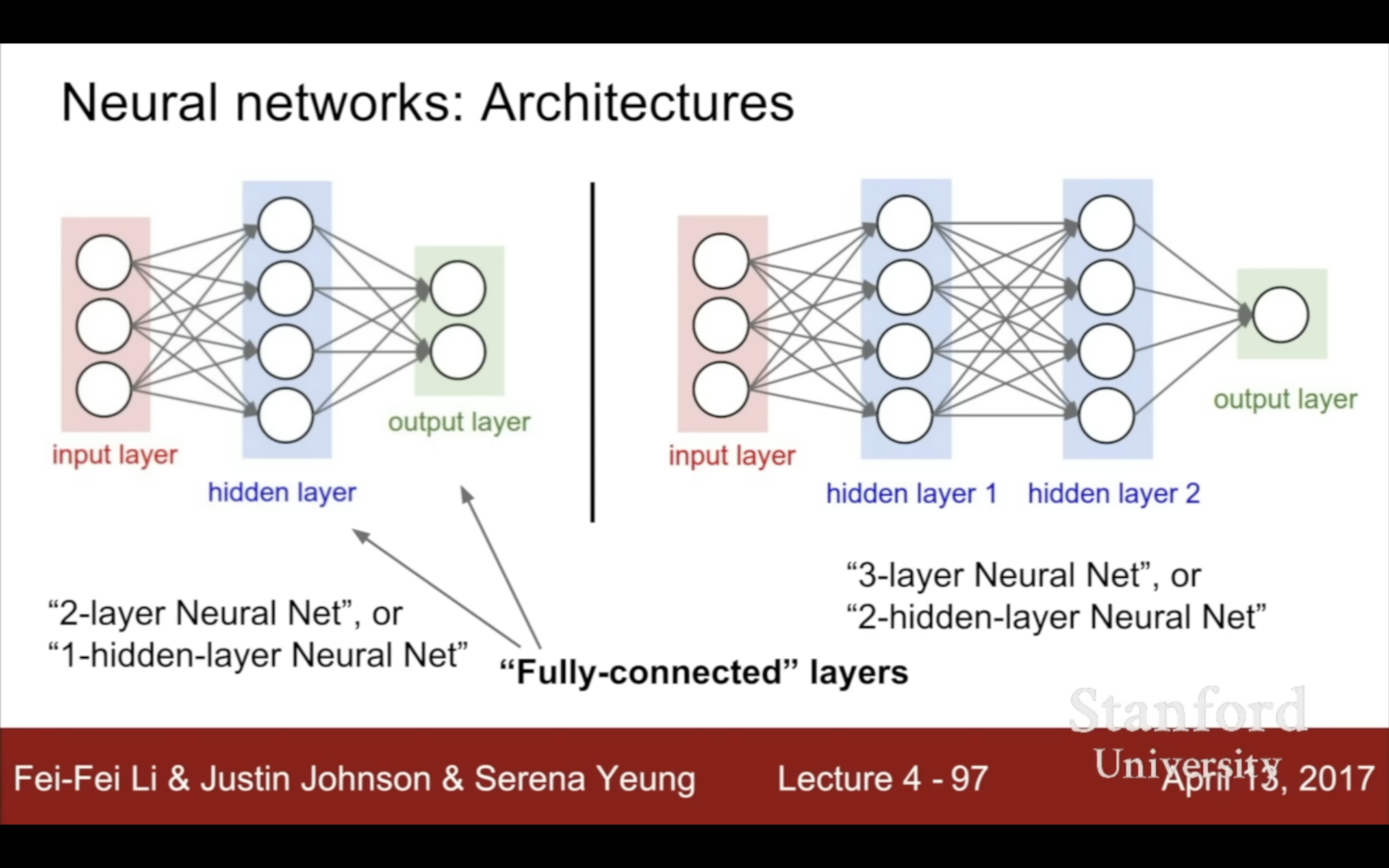 |
上面這個3-layer的代碼就像這樣:# **forward-pass of a 3-layer neural network:**
f = lambda x: 1.0/(1.0 + np.exp(-x)) # activation function (use sigmoid)
x = np. random. randn(3, 1) # random input vector of three numbers (3x1)
h1 = f(np.dot(Wl, x) + bl) # calculate first hidden layer activations (4x1)
h2 = f(np.dot(W2, h1) + b2) # calculate second hidden layer activations (4x1)
out = np.dot(W3, h2) + b3 # output neuron (1x1)
關於polynomial regression,
多项式回归模型本身是非线性的,因为它涉及到自变量的高次方,能够拟合非线性数据关系。然而,多项式回归模型仍然可以被视为线性模型的一种,原因在于模型参数的估计和模型预测都可以通过线性回归的方法实现。
具体来说,在多项式回归模型中,自变量的高次方可以视为新的特征,将其添加到原始特征中,从而将非线性问题转化为线性问题。然后,使用线性回归模型估计模型参数(即新特征的系数),并使用线性回归模型进行预测。
因此,多项式回归模型被称为线性模型的扩展,它可以用于拟合非线性数据关系,并且可以使用线性回归的方法进行参数估计和预测。
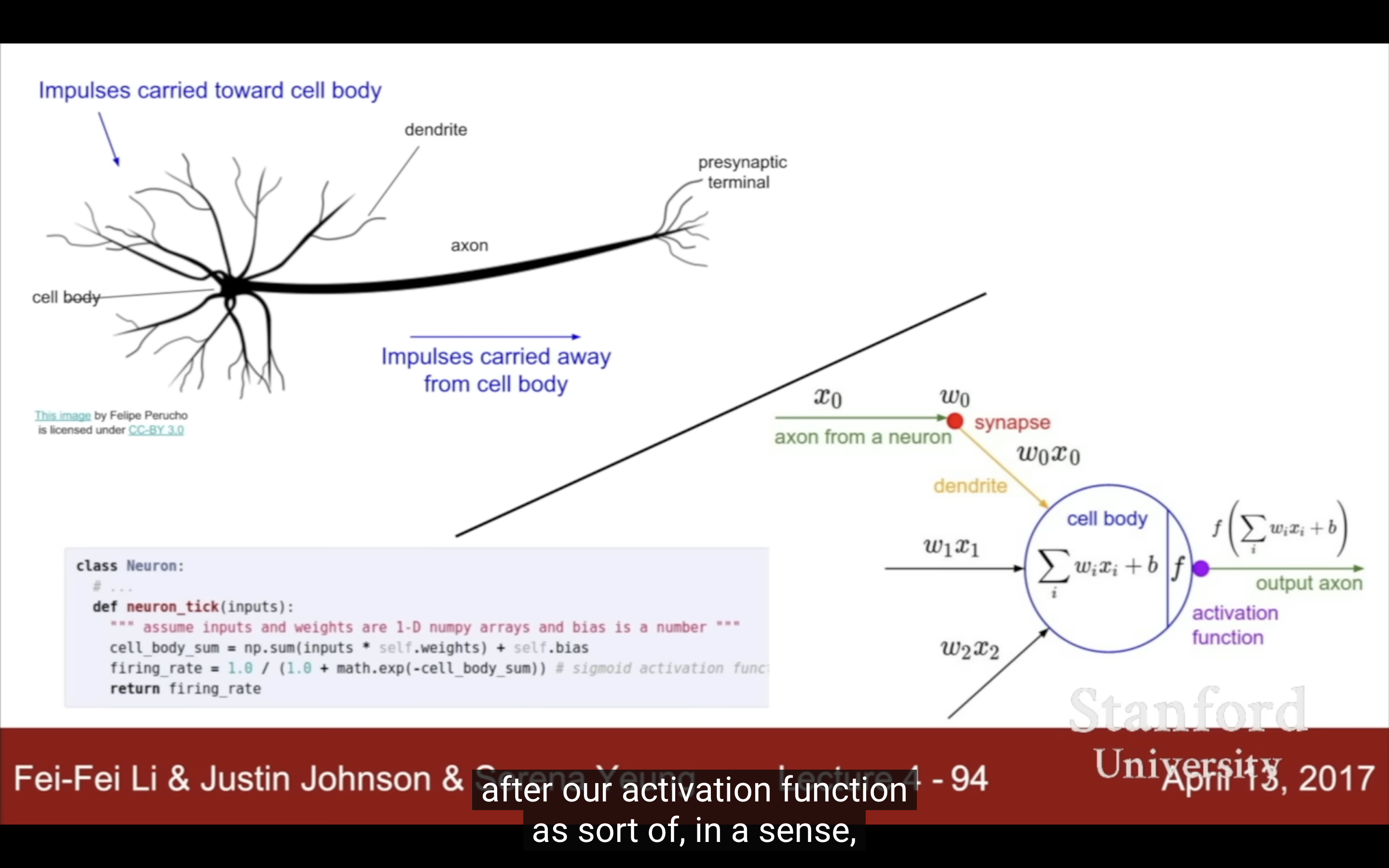
| Serena說relu是最接近實際神經的activation function | |
|---|---|
 |
 |
Lecture 5
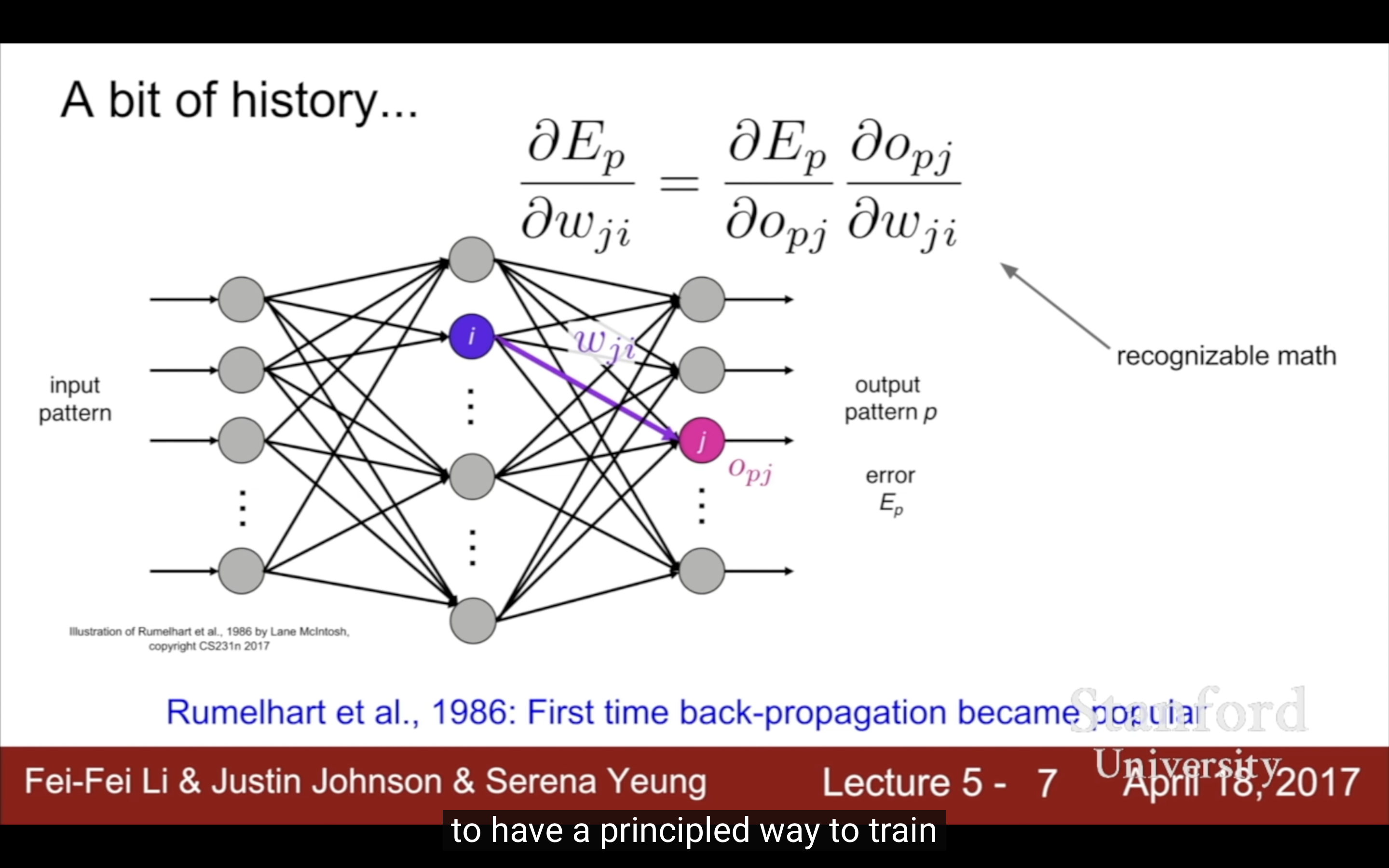
| 1986 backprop | 1998 first example backprop/gradient based cnn | 2012 Alex Krizhevsky |
|---|---|---|
 |
 |
 |
CNN的卷積
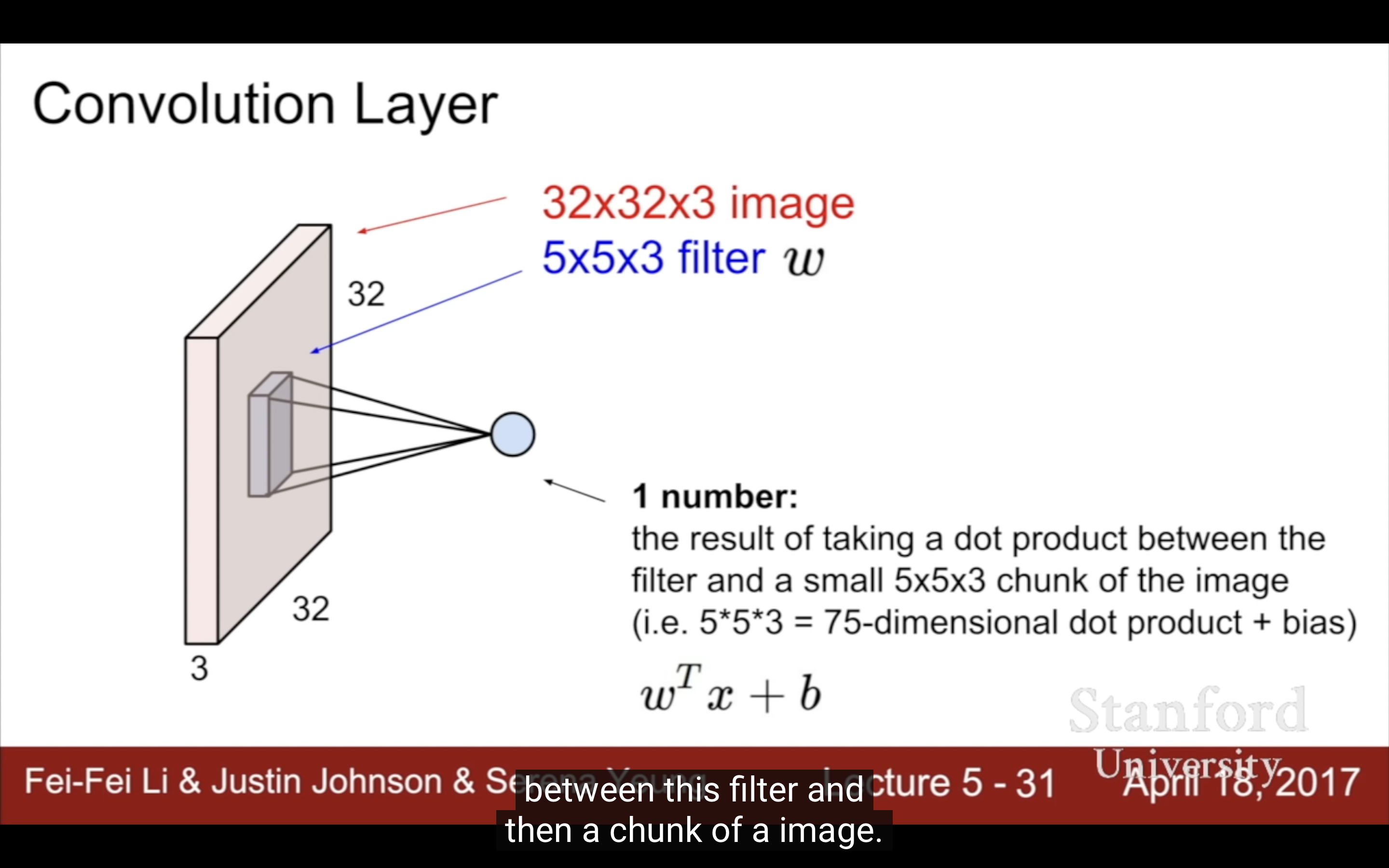
each filter is looking for a specific type of template or concept of the input volume.
有個問題問得很好,what’s the intuition for increasing the depth each time. 每一層讓filter更多activation map更深(3、6、…)是實踐裡大家發現的更好的設定而已,cnn有很多design choice,比如filter size啥的。
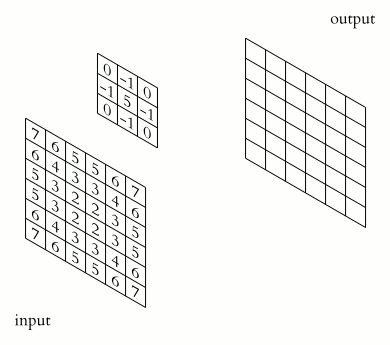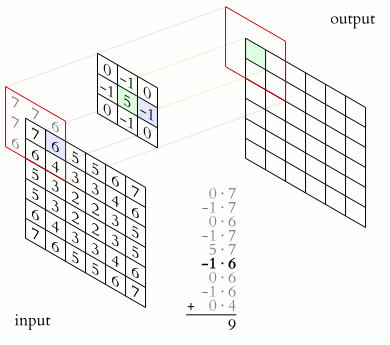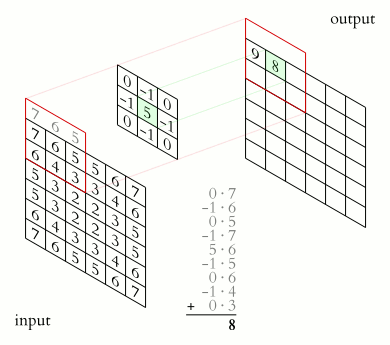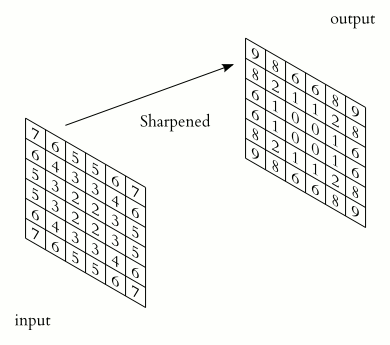
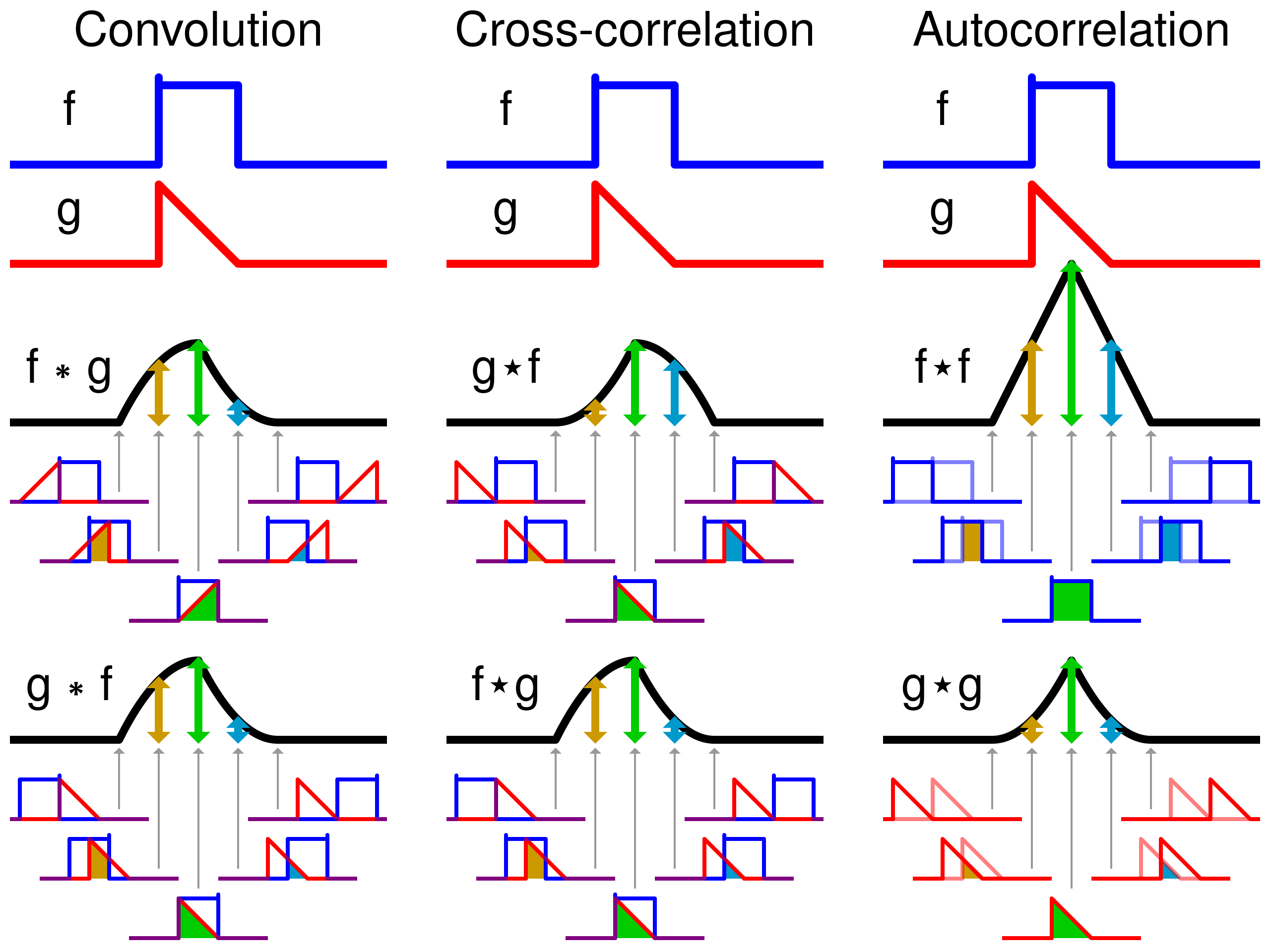
信號處理的卷積計算signal processing convolution
假设两个简单的离散信号 $f(t)$ 和 $g(t)$,它们的取值如下:
步骤 1:反转信号 $g(t)$
首先将 $g(t)$ 反转,得到 $g(-t)$:
然後就可以想像是這個反轉的 g 在 f 上滑動了。
步骤 2:滑动并计算乘积
当 t = 0 时:
当 t = 1 时:
当 t = 2 时:
由于 $g(t)$ 在 $t = 2$ 时没有定义,所以 $g(2) = 0$,于是:
当 t = 3 时:
同样,$g(2) = 0$,因此:
当 t = 4 时:
最终卷积结果
因此,卷积的结果 $(f * g)(t)$ 为:
其中卷积结果的最大时间点是由 $f(t)$ 和 $g(t)$ 的最远时间点组合而成。具体来说,卷积的结果最大会到达:
例如,假设 $f(t)$ 的最后一个有效时间点是 $t = 2$,而 $g(t)$ 的最后一个有效时间点是 $t = 1$,则:
这样,卷积的最大时间点 $t_{\text{max}}$ 为 3。
- 跟cnn的卷積一樣的是:都要想像成滑動操作,信號卷積是二維的兩條線滑動;
- 不一樣的是:cnn不需要反轉,而(f *g)(t)裡後面這個函數要先在時間軸上反轉。
deconvolution反卷積
上面的 $f(t) = [1, 2, 3]$ 是原始信號(可能是圖像像素值、音頻信號幅度),$g(t) = [4, 5]$ 叫做模糊核(比如是一個濾波器、噪聲源),得到的線性無填充的卷積結果 $y(t) = [4, 13, 22, 15, 0]$ 。
反卷積就是通過模糊核 $g(t)$ 和卷積結果 $y(t)$ 恢復原始信號 $f(t)$ 的過程,可以用傅里叶变换或卷积定理,在实际应用中,反卷积操作通常需要一些数值优化算法来求解,因为恢复信号可能涉及更复杂的卷积核和信号。
- 卷积:信号与某个模糊核进行卷积,导致信号被模糊处理。
- 反卷积:给定模糊后的信号和模糊核,通过数学方法恢复出原始信号。
用這個網站可以在線算信號卷積。
這節課原來後面講了如何可視化模型學到的特徵。(basically each element of these grids is showing what in the input would look like that basically maximizes the activation of the neuron. So in a sense, what is the neuron looking for?)
| 不這樣設置stride | formula,但其實豎直方向上也可以有stride,ouput size又是另外的formula | padding(zero,mirror,and so on)能保持activation size,input和ouput一樣size,但是stride>1的作用呢?是避免边缘信息丢失 |
|---|---|---|
 |
 |
 |
| example2 | 1x1 conv filter是可行的 | torch的一個conv |
|---|---|---|
 |
 |
 |
stride越大downsampling就越多,參數越少模型越小,包括所有參數一直到FC連接的值也會變少。(tradeoff)
| pooling,不影響depth | stride設大就是downsampling,跟pooling效果是一樣的 |
|---|---|
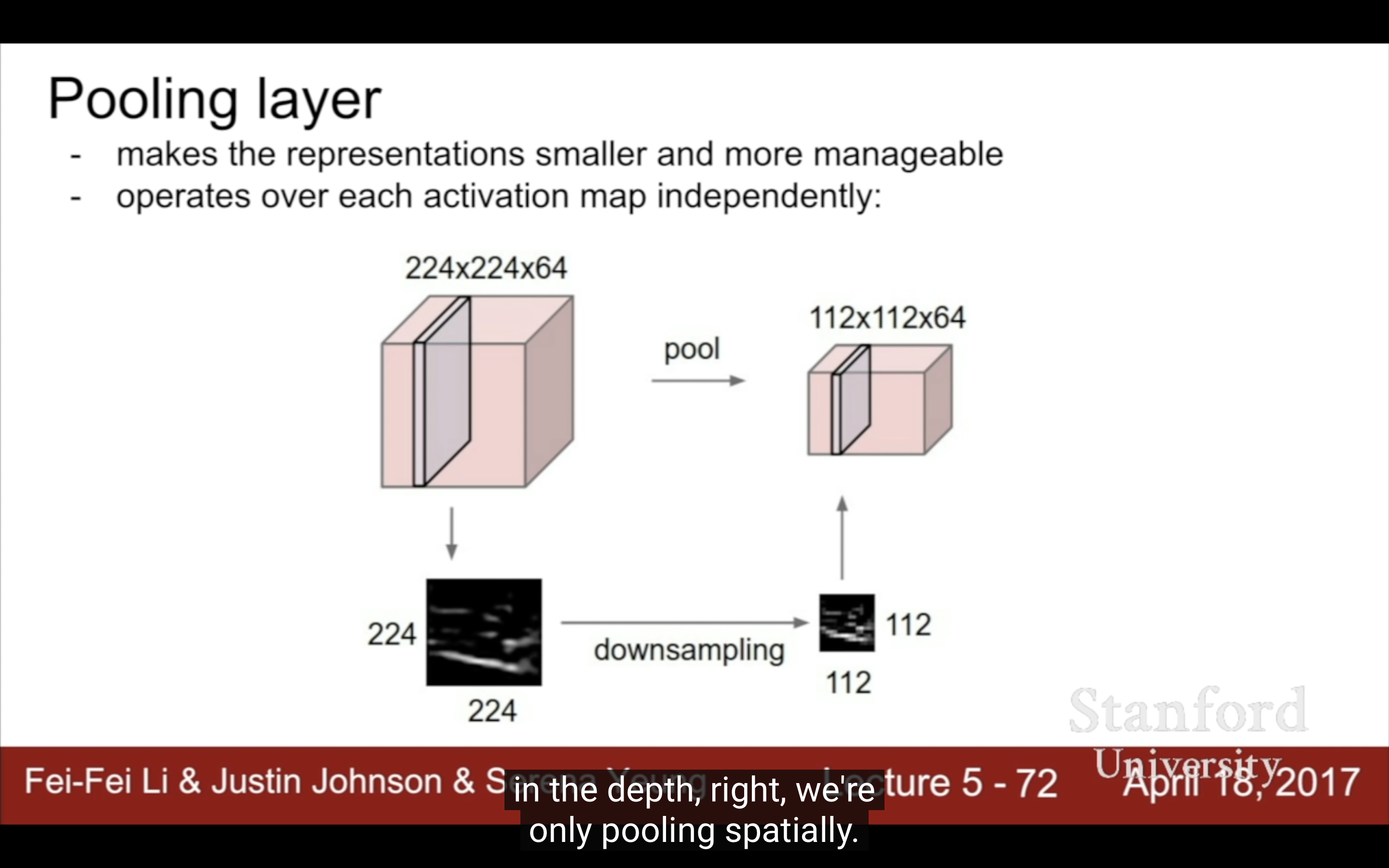 |
 |
右圖為什麼downsample太快不好?那為什麼還要pooling?現在不缺算力追求越多參數越好是不是不再需要太多downsample了?
這個問題可以再問chatgpt,回答得挺好,1.前幾層下採樣太快會丟失很多信息;2.pooling減少計算量即使現在不缺算力還是需要,否則計算量迅速膨脹徒增開銷,用結果導向的思路來說不影響效果的情況下downsampling總是好的;3.pooling或者說設置較大stride、現代架構其他捕捉全局關係的方式,除了减少特征图尺寸減少參數量外,也能抑制過擬合。是一種regularization。
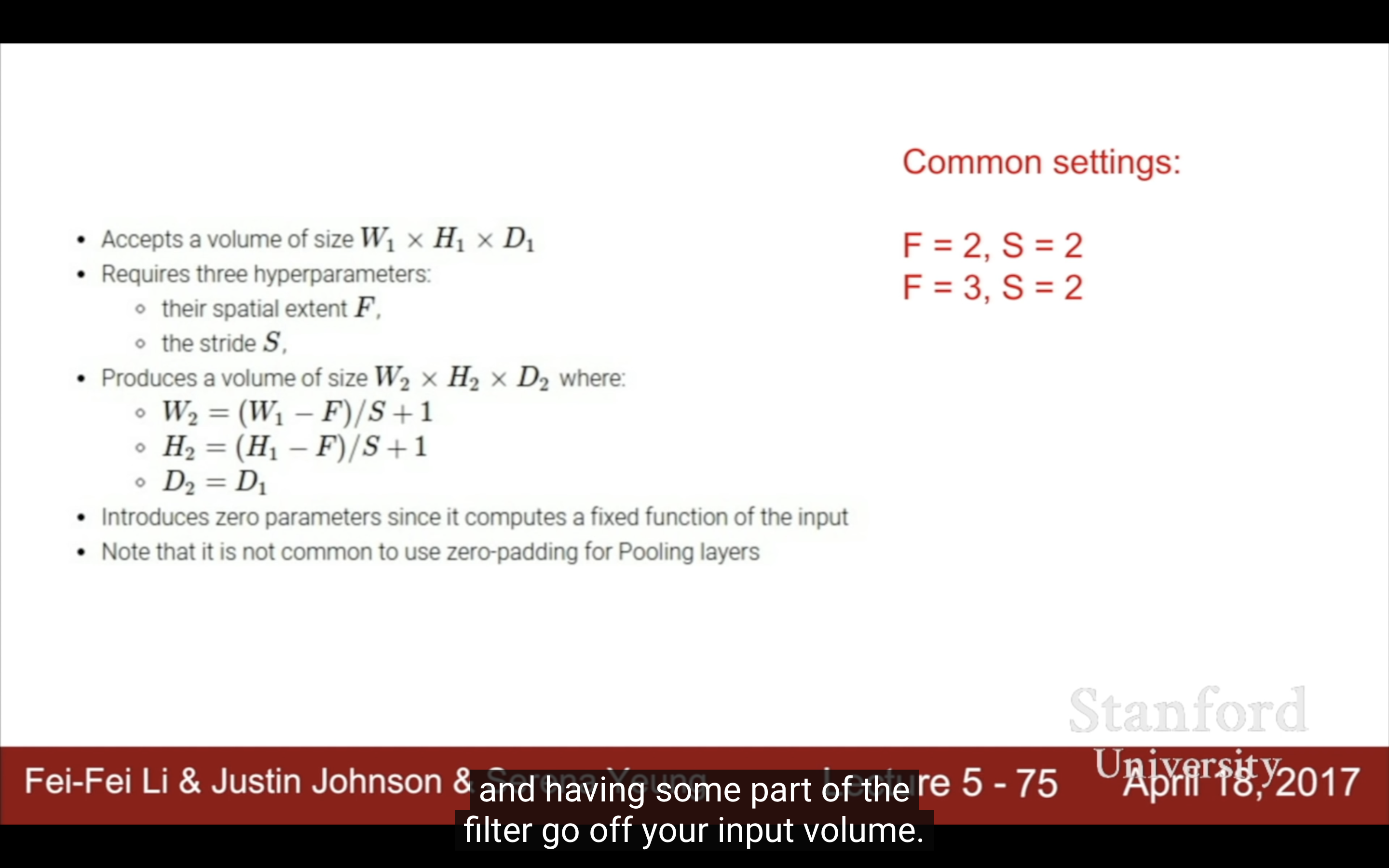
Pooling 层的 stride 是否一般设置为没有 overlap?
在卷积神经网络(CNN)中,Pooling 层的 stride 是否设置为没有 overlap(即步长等于池化窗口大小)通常取决于网络设计的需求。一般来说,Pooling 层的 stride 通常设置为没有 overlap,即步长与池化窗口大小相同。具体解释如下:
没有重叠(No Overlap):
- Stride = Pooling窗口大小:这是最常见的设置,意味着池化操作的步长与池化窗口的大小相同,从而池化窗口之间没有重叠。
- 例如,在 2x2 的池化窗口下,stride = 2 会导致每次池化窗口滑动两个像素,池化窗口之间没有任何重叠区域。
优点:
- 计算效率更高:没有重叠的池化可以减少特征图的尺寸,降低计算复杂度。
- 避免冗余计算:每次池化操作处理的区域都是唯一的,因此没有重复计算的部分。
有重叠(Overlap):
- Stride < Pooling窗口大小:在某些情况下,池化窗口之间会有重叠。例如,使用 2x2 的池化窗口和 stride = 1,池化窗口会覆盖有重叠的区域。
优点:
- 保留更多细节:有重叠的池化可能会保留更多的特征,尤其是在需要更精细特征提取时。
缺点:
- 计算量更大:重叠池化会增加计算开销,导致计算效率较低。
结论:
- 在大多数情况下,Pooling 层的 stride 被设置为没有重叠,尤其是在经典的卷积神经网络(如 LeNet、VGG)中。这样可以高效地减少特征图的尺寸,并降低计算量。
- 在某些特殊任务中(例如,需要更细致特征提取的任务),也可以选择有重叠的池化。
為什麼max pooling比average pooling更commonly used?
- 实践效果更好。在大量的实际实验中,使用 Max Pooling 的 CNN 通常比使用 Average Pooling 的 CNN 效果更好,尤其是在分类和目标检测任务中。这也是 Max Pooling 被更广泛应用的原因之一。
- 更好地保留关键信息。Max Pooling 选择每个池化窗口中的最大值,从而保留了特征图中的最显著特征。这种方式在提取边缘、纹理等重要特征时非常有效。相比之下,Average Pooling 是取平均值,可能会平滑掉重要的边缘信息,导致信息丢失。
- 具有更强的平移不变性。Max Pooling 能更好地处理位置的微小变化(平移不变性),因为它仅保留每个窗口的最大值,对其他不显著的特征不敏感。这在处理图像时有利于使网络对物体位置的微小变动更加鲁棒。

訓練例子:https://cs.stanford.edu/people/karpathy/convnetjs/demo/cifar10.html
通常只有第一層activation maps能被解釋,越高層越難解釋。
- There is a trend towards smaller filters and deeper architectures
- There is a trend towards getting rid of POOL/FC layers (just CONV)
- Typical architectures look like:
[(CONV-RELU)*N-POOL?]*M-(FC-RELU)*K,SOFTMAX
where N is usually up to ~5, M is large, 0 <= K <= 2. - but recent(2017) advances such as ResNet/GoogLeNet challenge this paradigm
Lecture 6
- Activation Functions(non-linearity)
- Data Preprocessing
- Weight Initialization
- Batch Normalization
- Babysitting the Learning Process
- Hyperparameter Optimization
Activation Functions(non-linearity) 为什么输入要正负样本均衡?
gradient on w這個說法指的是$\frac{\partial L}{\partial w}\ or\ \nabla_w L$。(或者df/dw)

| backprop反向傳播回來的value可以光看曲線不用公式,平緩的地方導數為0(forward pass就看函數曲線本身,backward就看曲線變化,高中數學),(sigmoid gate, a node in computational graph) | 講得太好了這裡 |
|---|---|
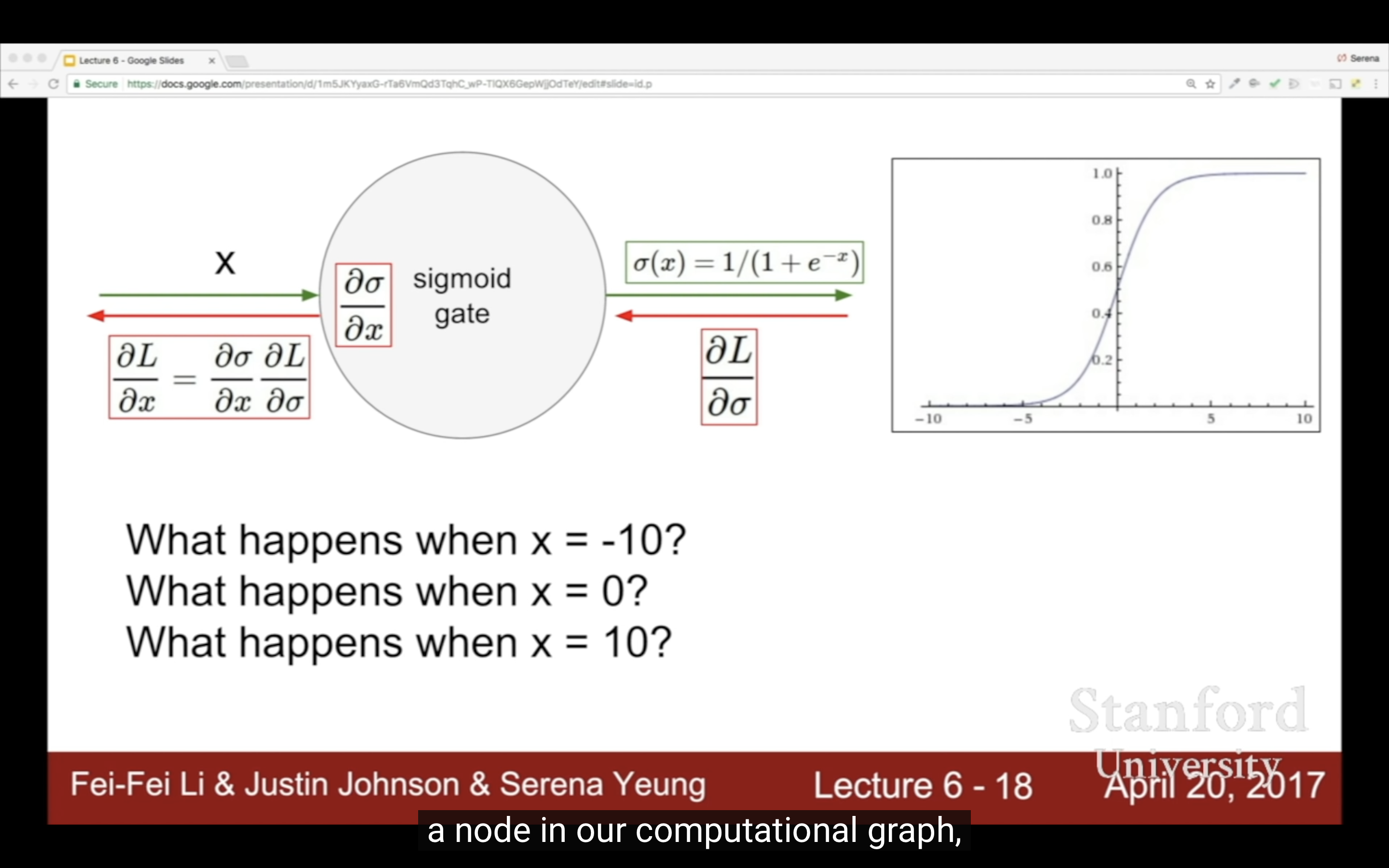 |
 |
- sigmoid
- 3 problems:
- Saturated neurons “kill” the gradients:(注意這裡說的是激活函數這個node的gradient,只有一個自變量)
- x = -10, sigmoid(x) = 0, sigmoid’(x) = (1-0)0 = 0
- x = 0, sigmoid(x) = 1/2, sigmoid’(x) = (1-1/2)1/2 = 1/4
- x = 10, sigmoid(x) = 1, sigmoid’(x) = (1-1)1 = 0
- Sigmoid outputs are not zero-centered: 如下图(這裡說的是激活函數之前score function node,有W和X倆自變量)
- 如果一个神经元的输入X全是正的,gradients on w即dL/dw = dL/df * df/dw(其中df/dw=x)就全是正的或者负的,就会导致graident只向全正和全负更新,最优化W的过程就会很低效。
- 这也是为什么x最好positive和negative均衡,因为如果输入数据X本身就是全正的,那不需要sigmoid激活函数压缩就已经会导致图里的zig zag path问题了。
- 而sigmoid激活函数就是这样一个会把输入全部拉到0~1的玩意。
- exp() is a bit computationally expensive
- Saturated neurons “kill” the gradients:(注意這裡說的是激活函數這個node的gradient,只有一個自變量)
- 3 problems:
- tanh(x)解决了zero-centered的问题,但还是存在梯度消失问题,而且计算开销比sigmoid更大因为有更多exp运算。$\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$
- ReLU(Rectified Linear Unit), f(x) = max(0, x)
- pros:(上面的饱和函数、计算开销問題都解決了)
- Does not saturate (in region).
- Very computationally efficient
- Converges much faster than sigmoid/tanh in practice (e.g. 6x faster) 收斂更快
- Actually more biologically plausible than sigmoid
- 2012 Alex Krizhevsky第一次使用
- cons:
- zero-centered問題還是存在
- dead relu
- Dead ReLU 问题是指在使用 ReLU (Rectified Linear Unit) 激活函数时,某些神经元可能在训练过程中始终输出零,这些神经元被称为“死神经元”。这种情况通常发生在 ReLU 的输入为负值时,ReLU 会将其输出设置为零。长期处于这种状态的神经元无法进行有效的训练或更新,从而导致 死 ReLU 问题。
- 虽然 Dead ReLU 问题是存在的,但它在实际应用中通常并不严重,
- 神经网络中往往有足够的神经元来弥补死神经元的影响。
- 死神经元不会影响其他神经元的梯度传播。
- 使用 改进版 ReLU 激活函数(如 Leaky ReLU 或 PReLU)可以有效避免死神经元问题。
- pros:(上面的饱和函数、计算开销問題都解決了)
- Leaky ReLU / PReLU
- Leaky ReLU
- f(x) = max(0.01x, x)通常是0.01
- will not “die”.
- PReLU(Parametric ReLU)
- f(x) = max(αx, x)
- α是通過backprop/gradient descent訓練得到的,可是α如果學成負數,包括下面的ELU激活函數,都可能讓輸出全部變成正數,跟sigmoid一樣的問題
- α是不是每個neuron都不一樣?Serena也記不清了。chatgpt說是每個都獨立,沒有全局alpha,那這樣的話α學成負數就不是什麼問題了,大概會是偶然現象
- ELU(Exponential Linear Units)
- pros
- All benefits of RelU
- Closer to zero mean outputs
- Negative saturation regime compared with Leaky ReLU adds some robustness to noise
- cons
- exp() computation
- pros
- maxout neuron
- $f(x) = \max \left( W_1^T x + b_1, W_2^T x + b_2, \dots, W_k^T x + b_k \right)$
- Does not have the basic form of dot product -> nonlinearity
- pros:
- Generalizes ReLU and Leaky ReLU
- Linear Regime!(線性狀態(線性區間)) Does not saturate! Does not die!
- cons:
- doubles the number of parameters/neuron
怎麼理解“activate”激活?這節課原來後面講了如何可視化模型學到的特徵。(basically each element of these grids is showing what in the input would look like that basically maximizes the activation of the neuron. So in a sense, what is the neuron looking for?上面這段看看
Data Preprocessing
| zero-mean就是因為上面的原因,也有別的PCA(decorrelate)和Whitening | 圖片說是一般不用normalize,只減去均值,減所有channels和per-channel結果上沒區別 |
|---|---|
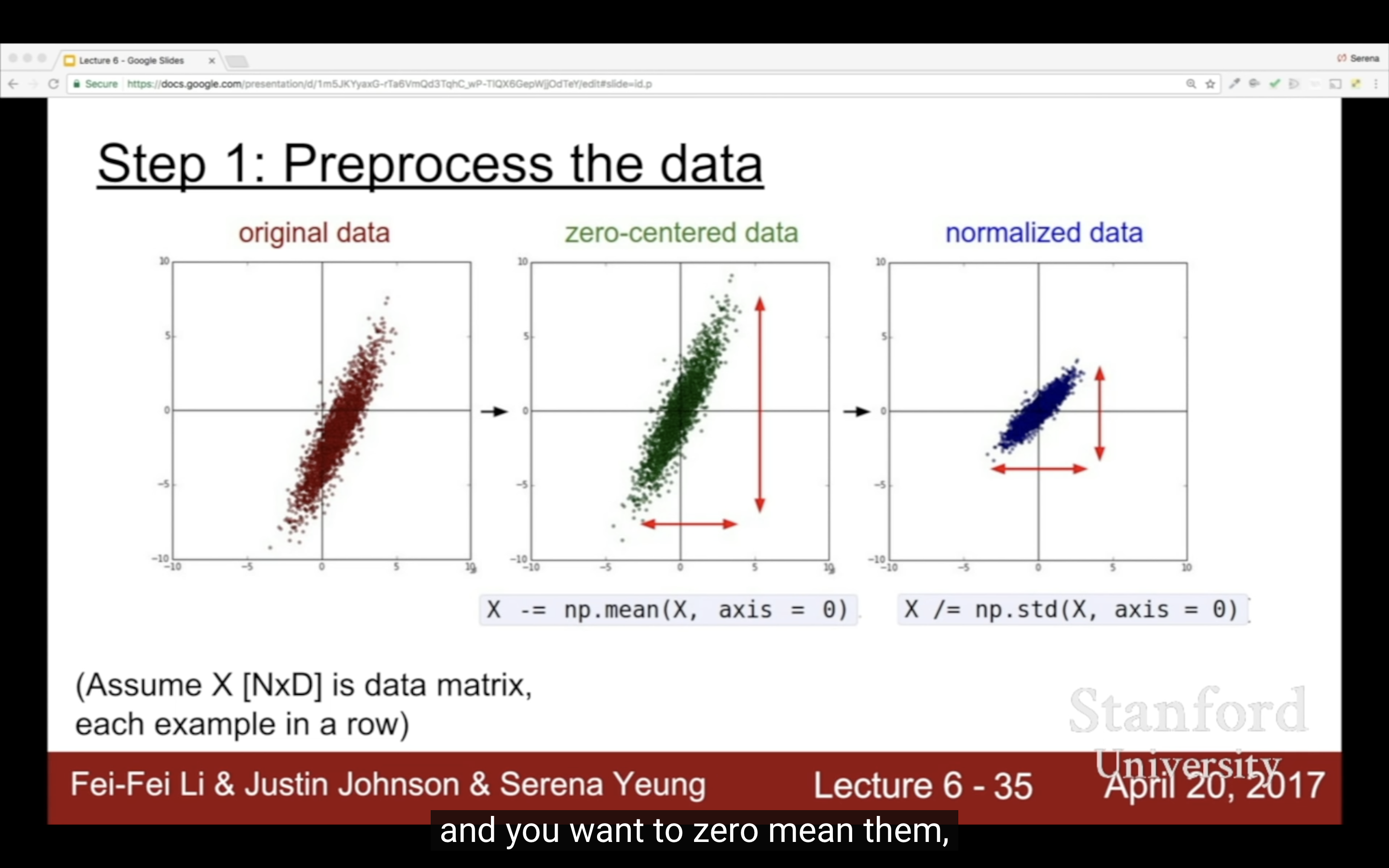 |
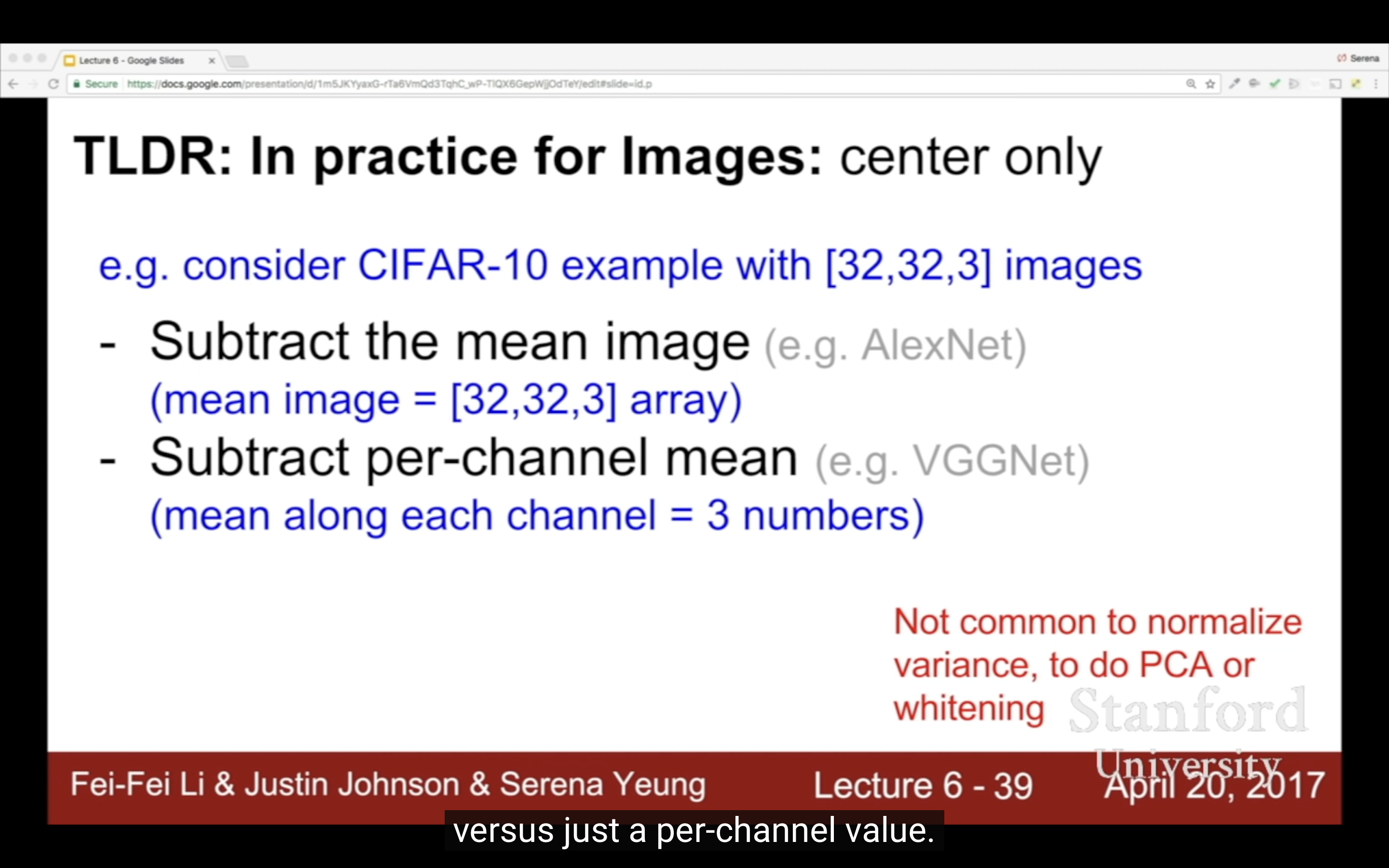 |
注意,trainning set上做的preprocess,test set也要做。注意是訓練階段得到的均值,而不是测试数据本身的均值。
上面的兩種方法:
- 计算训练集中的所有图像的像素值的均值,得到一个 全局均值图像,然後所有图像的每个像素都减去训练集中的所有图像在该像素位置的均值;
- RGB三個通道分別算均值,這倆方法可以取足夠量的數據算一個值,只要能代表總體分布就行不用完全全部數據。
Weight Initialization
- First idea: Small random numbers (gaussian with zero mean and 1e-2 standard deviation)
- W = 0.01 * np. random. rand (D,H)
- Works ~okay for small networks, but problems with deeper networks.
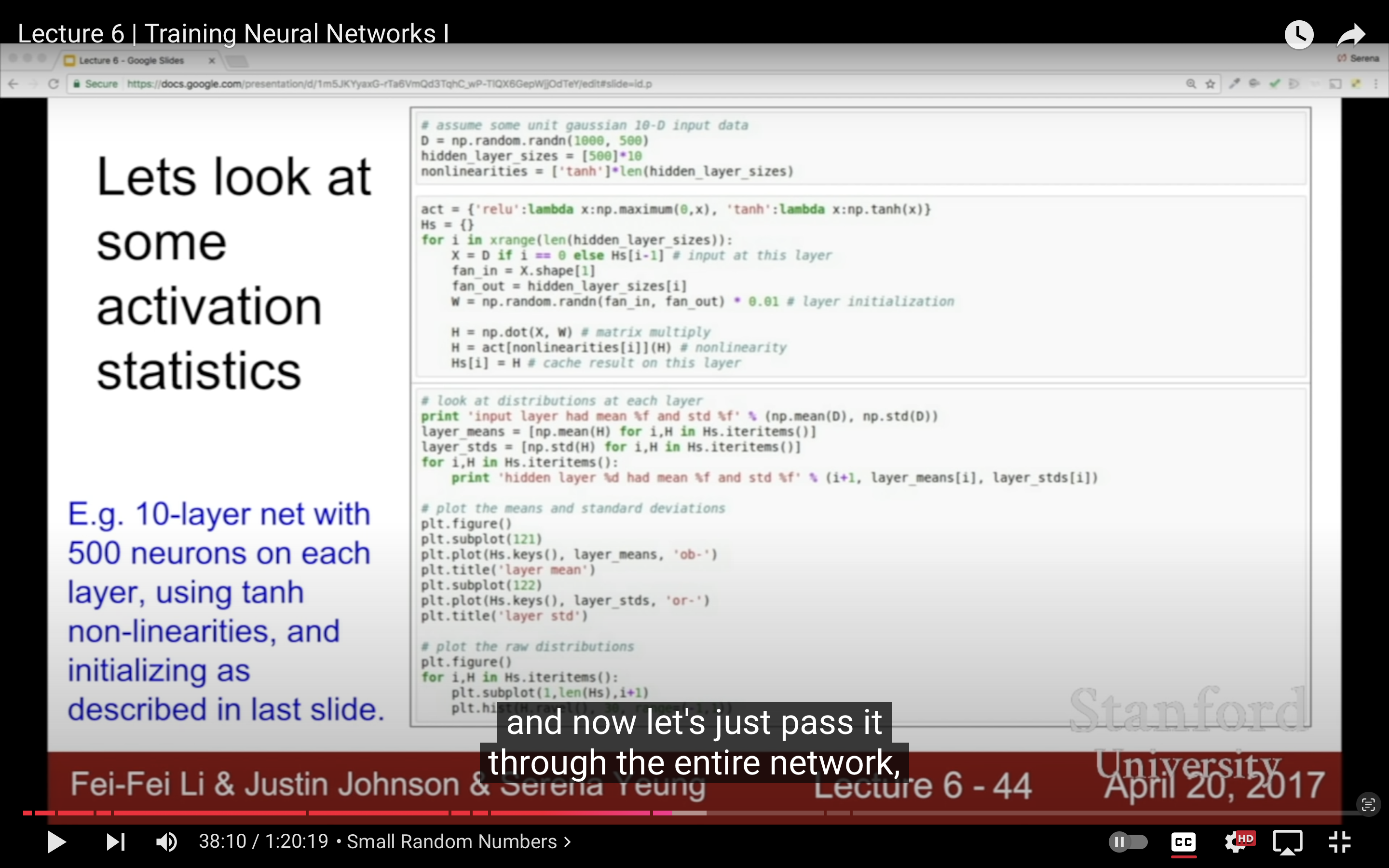
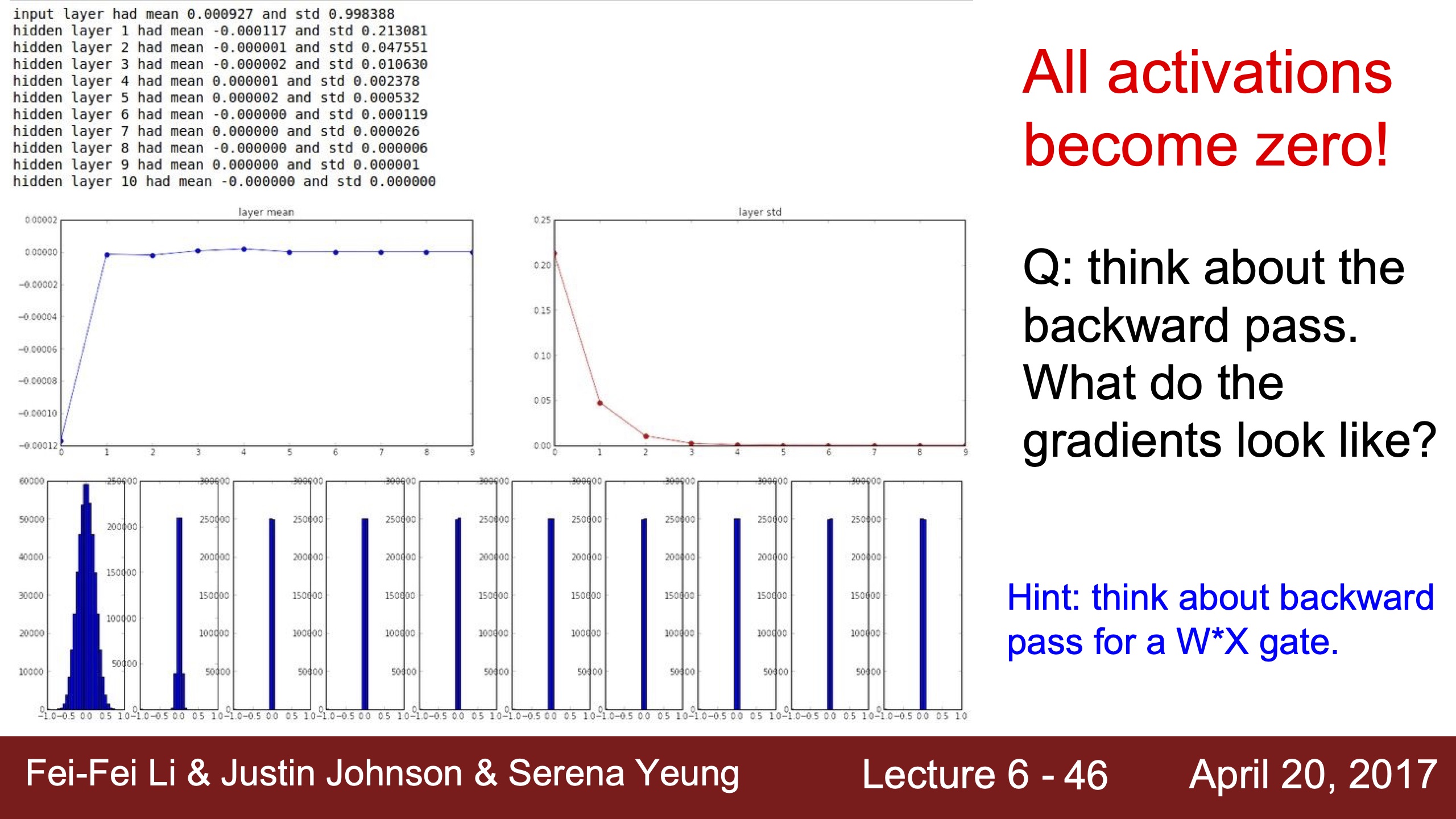
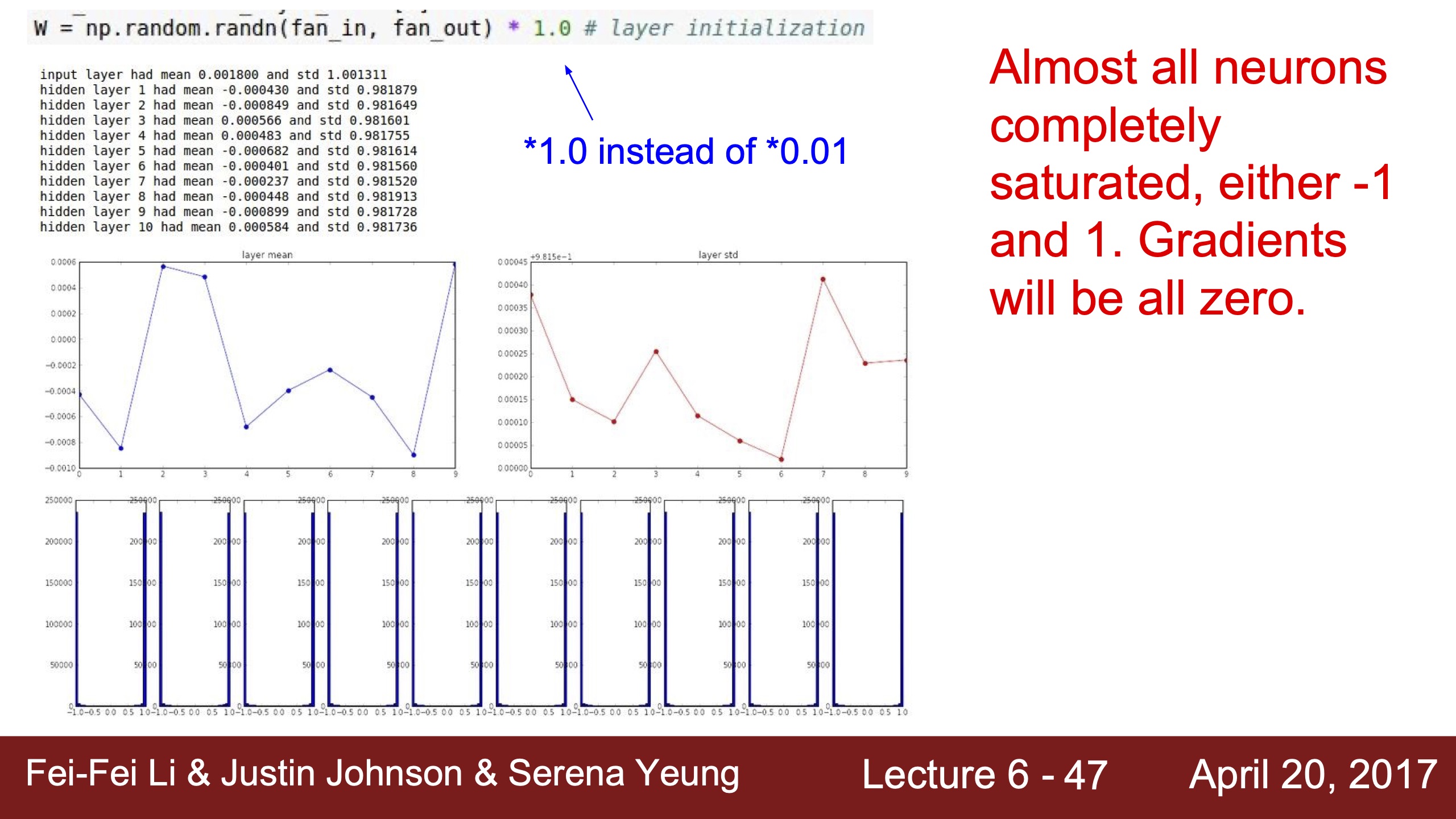
| First Idea activation layer visualization, 結果為右 | 這裡的gradients跟前面一樣也是dLoss/dW=X,這裡的激活層值全為0,所以梯度完全沒有更新 | 不用0.01而x100倍用1.0的初始化W的話,因為用的是tanh,到了激活函數的飽和區間,tanh飽和區間斜率幾乎是0,所以梯度也會消失 |
|---|---|---|
 |
 |
 |
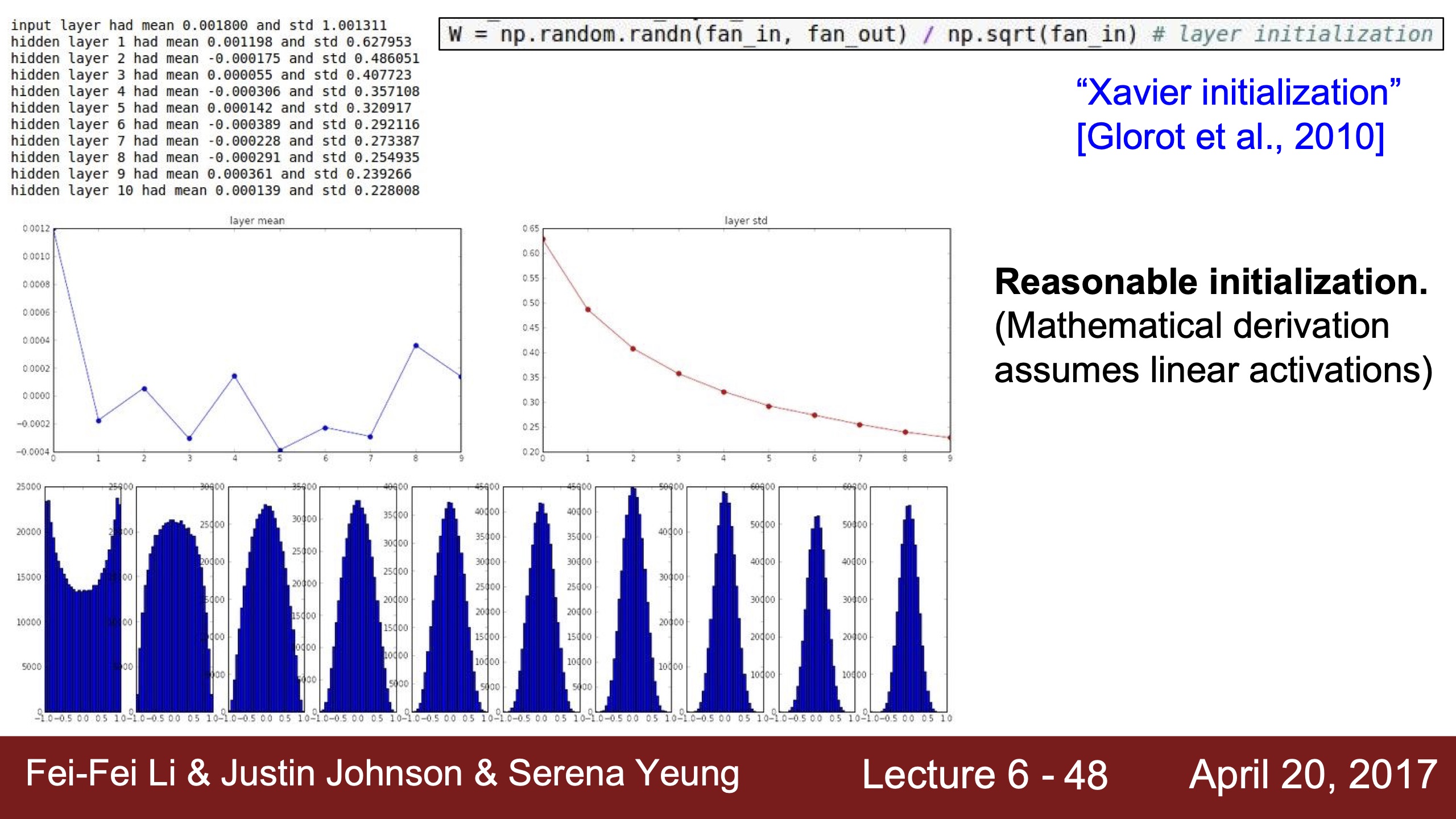
| xavier initialization用tanh,因為tanh在0處斜率很大,所以是梯度很有效的區域 | 用relu就梯度消失了,這裡雖然上面的mean也是0,但是relu在0處沒有斜率,沒有梯度,所以神經元也是deactivated | 用He初始化就變成我們想看到的分布,下面分布圖一樣是因為x拉太長了,上面的mean均值在0.5,是relu很有效的斜率gradient為1的線性區域 | 2017年仍是個活躍研究領域,不知道現在如何? |
|---|---|---|---|
 |
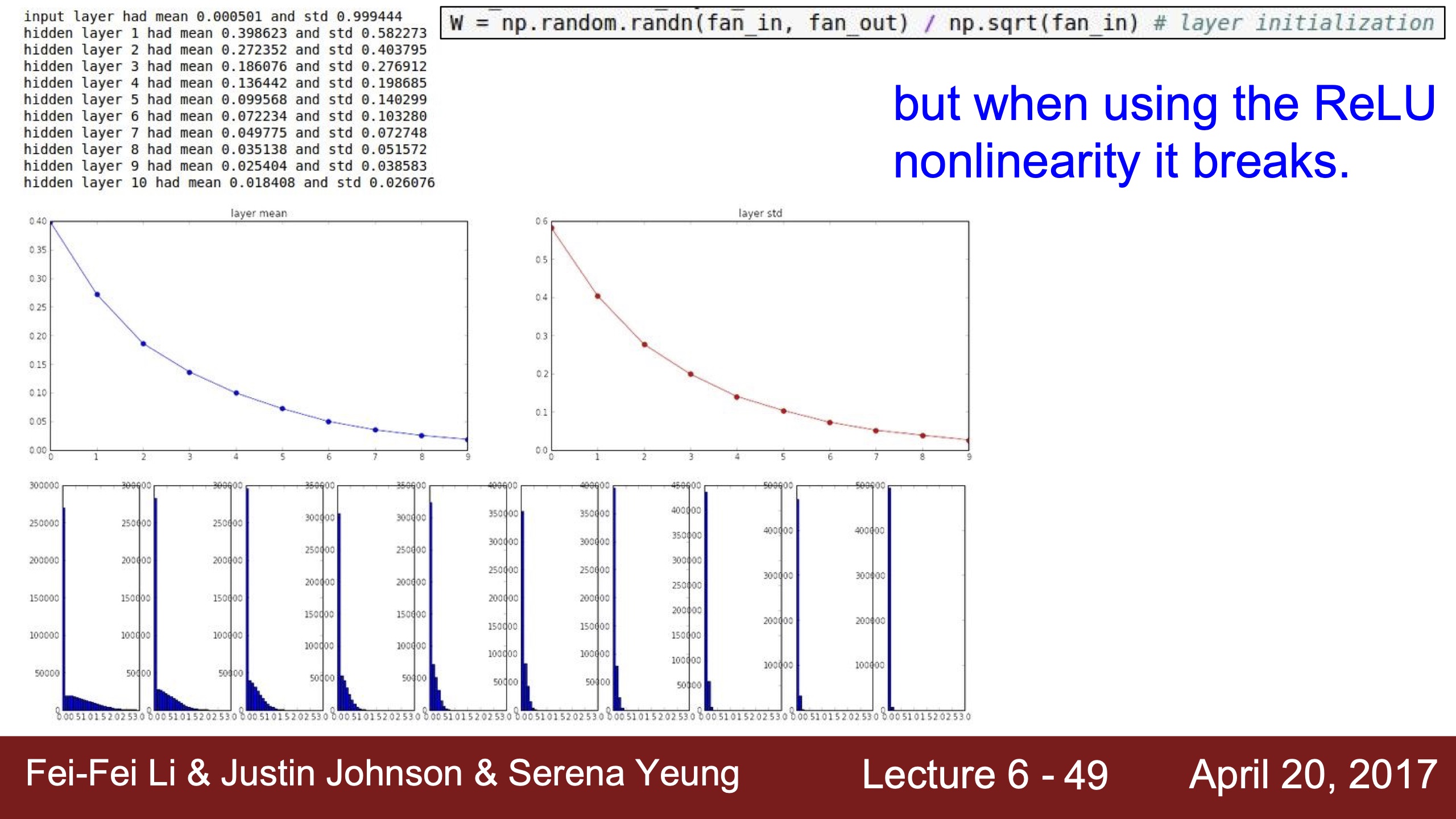 |
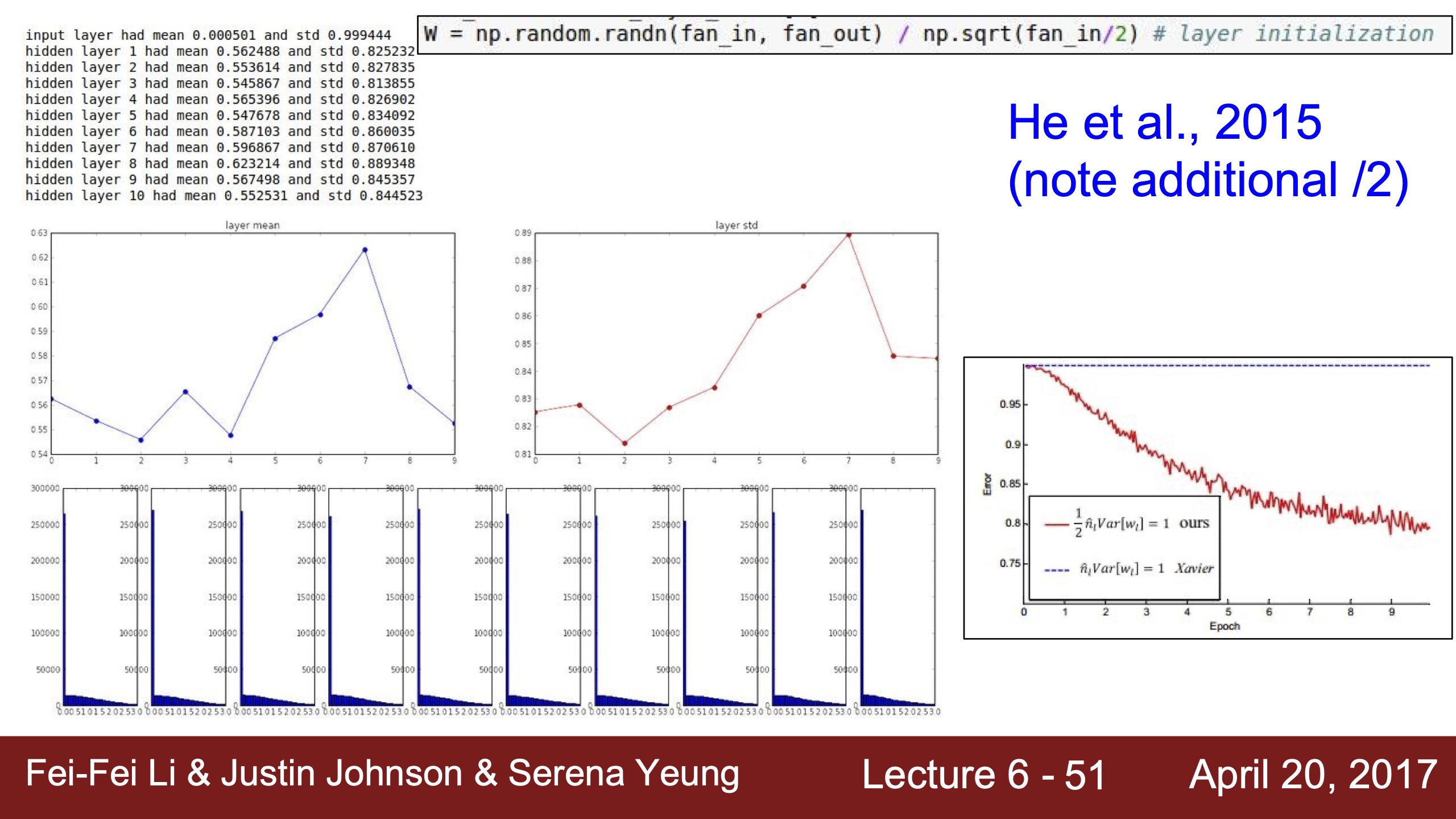 |
 |
Batch Normalization
We wants to keep activations in a gaussian range, like above, so use BN.
關於BN我的思考:
四年前就assginment卡在这没继续了,这次可好好搞明白。其实这部分跟上面找比较好的初始化W,以使每一层输入的分布都在神经元的有效区间内是一样的道理,有效区间就是tanh的0附近,relu的正数线性区间,斜率=1,即能让梯度反向传递回去。
BN有幾個核心目的,(去他媽媽的减小内部协变量偏移(Internal Covariate Shift))i.加速训练过程;ii.正则化作用(因為引入了小噪聲,噪聲指讓數據分布改變了?Serena的說法是,之前activation neuron只會考慮一個input但現在的input都是被整個batch的其他特徵影響過的,但總之增強泛化不是BN的主要目的);iii.通過下面的#3.可以缓解梯度消失和梯度爆炸。
那麼只要搞懂為什麼normalization能加快收斂,就可以了——
- https://stats.stackexchange.com/a/437848 In Machine learning, how does normalization help in convergence of gradient descent?
- 考慮$f(w)=w_1^2 + 25w_2^2$,通過觀察可以發現有global minimum $w=[0,0]^\top$。這個函數的梯度是,假如learning rate 𝛼=0.035,$w^{(0)}=[0.5, 0.5]^\top,$ 梯度更新公式是$w^{(1)} =w^{(0)}-\alpha \nabla f\left(w^{(0)}\right),$
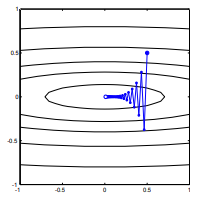 ,df/dw永遠會朝向w2的方向,可以想像w^2和25w^2這兩個曲線,變化速率相差太大(係數就是X),但經過normalization後,減去mean(12)除以σ = √Σ(x-x̄)2 / N = √144 = 12,可以標準化為$f(w)=-w_1^2 + w_2^2$,大概這麼理解下(這個分布只有兩個數據x1=1,x2=25所以感覺很怪),normalize後梯度變化會更朝向global minimum而不再zig zag。
,df/dw永遠會朝向w2的方向,可以想像w^2和25w^2這兩個曲線,變化速率相差太大(係數就是X),但經過normalization後,減去mean(12)除以σ = √Σ(x-x̄)2 / N = √144 = 12,可以標準化為$f(w)=-w_1^2 + w_2^2$,大概這麼理解下(這個分布只有兩個數據x1=1,x2=25所以感覺很怪),normalize後梯度變化會更朝向global minimum而不再zig zag。
batch normalization會根據不同的激活函數學習不同的參數嗎?比如對relu來說,希望輸入都在正數區間避免dead relu,比如tanh希望輸入不要到飽和區間。還是說batch normalization總是盡可能接近mean=0,deviation=1的標準正態分佈?
- 不一定?
- chatgpt說BN總是希望輸入/特徵的分布盡可能接近標準正態,只不過normalization之後,1.可以避免太多負值導致太多dead relu;2.可以避免太多值在tanh的-1和1飽和區間裡。這樣來看也還是很好的。
- 但Serena說通過學習γ和β參數,雖然BN本身是想讓分布變成標準正態分佈,但也給模型靈活度,可以主動不讓tanh飽和,或者搞出全正數分布不讓dead relu出現。
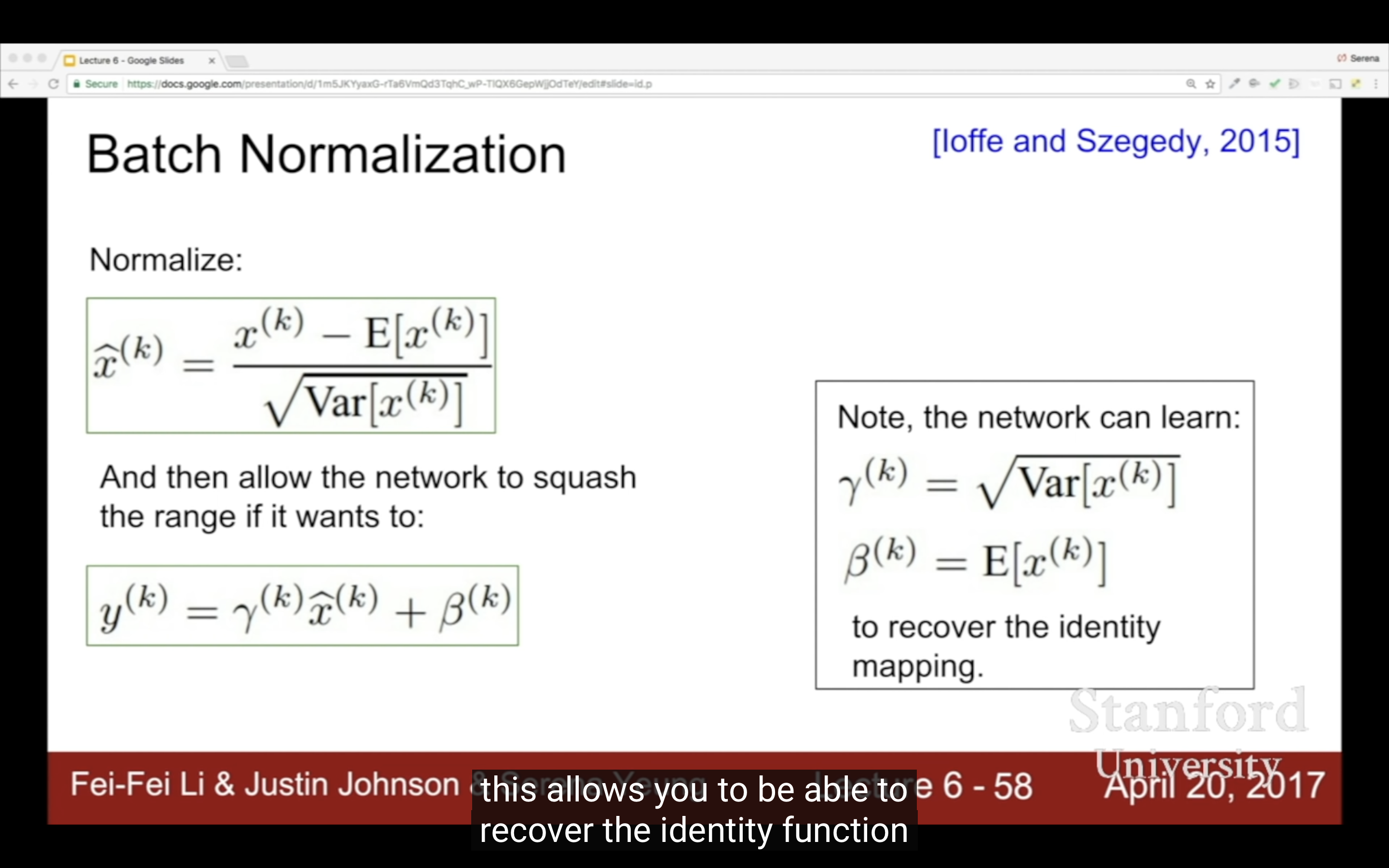
激活層/隱藏層的歸一化是輸入的歸一化,不是輸出的。
數據的歸一跟激活函數的歸一化/標準化是一樣的目的和道理,實際上就是因為數據normalization/standardization效果很好,那麼為什麼不把每一層的輸入值都歸一化/標準化?
BN 允许激活值的分布在训练过程中变化,并不强制要求它们是标准正态分布。尽管初始阶段会做标准化处理,但在学习过程中,BN 可以调整输出的均值和方差,导致输出分布变得更加灵活。
- 通过学习 γ 和 β 参数,BN 可能会产生一些不完全符合标准正态分布的分布,包括可能的偏移或变化,如全正分布等。
課程進行到1小時時同學問了我想問的問題,強迫features變成gaussian分布不會丟失信息讓數據失真嗎?CNN裡希望保持空間信息所以預處理不用normalization,對特徵圖activation maps其實不會失真,說只是shifting(- mean)和scaling(/ standard deviation)。
在测试时(Testing Phase):
- 在测试阶段,BN不再使用测试数据来计算均值和方差。相反,它会使用训练过程中通过各个mini-batch累计的全局均值和方差,每一层使用单独的全局均值和方差。
- 这样做是因为测试集的batch大小通常较小,直接计算时可能不稳定,且我们希望测试时模型的行为尽可能和训练时一致。
Babysitting the Learning Process
| 增強正則的時候,期望是loss變大(加了一項),debugging策略get✔。 | take the first 20 examples from CIFAR-10;turn off regularization (reg = 0.0);use simple vanilla ‘sgd’,用最簡單的設定確保模型能過擬合很少的樣本,讓loss趨近於0,debugging strategy get✔ | |
|---|---|---|
 |
 |
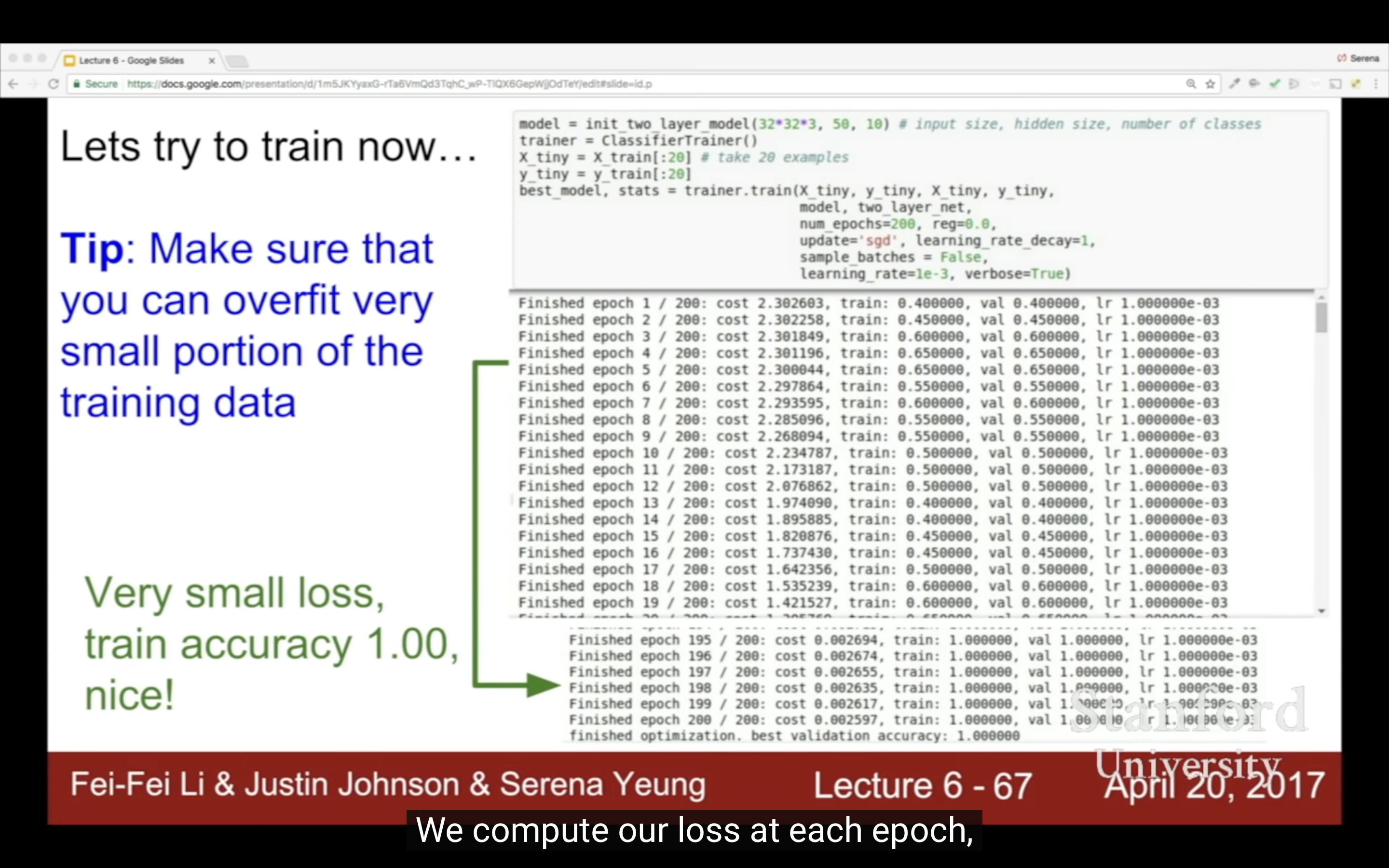 |
然後用小的正則來找合適的learning rate,最重要的超參,如果loss/cost變化太慢一般來說是learning rate太小了;loss變成nan就是越界了,learning rate太大,loss變成inf?
Hyperparameter Optimization
Cross-validation strategy,
先粗定大範圍,然後仔細尋找(coarse to fine search)。
justin在2017年會盡量避免一次搜索2到4個以上超參數,複雜度畢竟指數級增長。
Tip for detecting explosions in the solver:
If the cost is ever > 3 * original cost, break out early
| 沒懂為什麼用10的uniform冪為範圍 | 隨機的更好? |
|---|---|
 |
 |
| 之前OFA和學姐做的另一個忘了名字的模型我整天就調適這玩意 | CV就是這麼枯燥,我當時做小樣本都快做瘋了,小樣本那玩意太多實驗了(找ppt |
|---|---|
 |
 |
| 觀察曲線調參 | ||
|---|---|---|
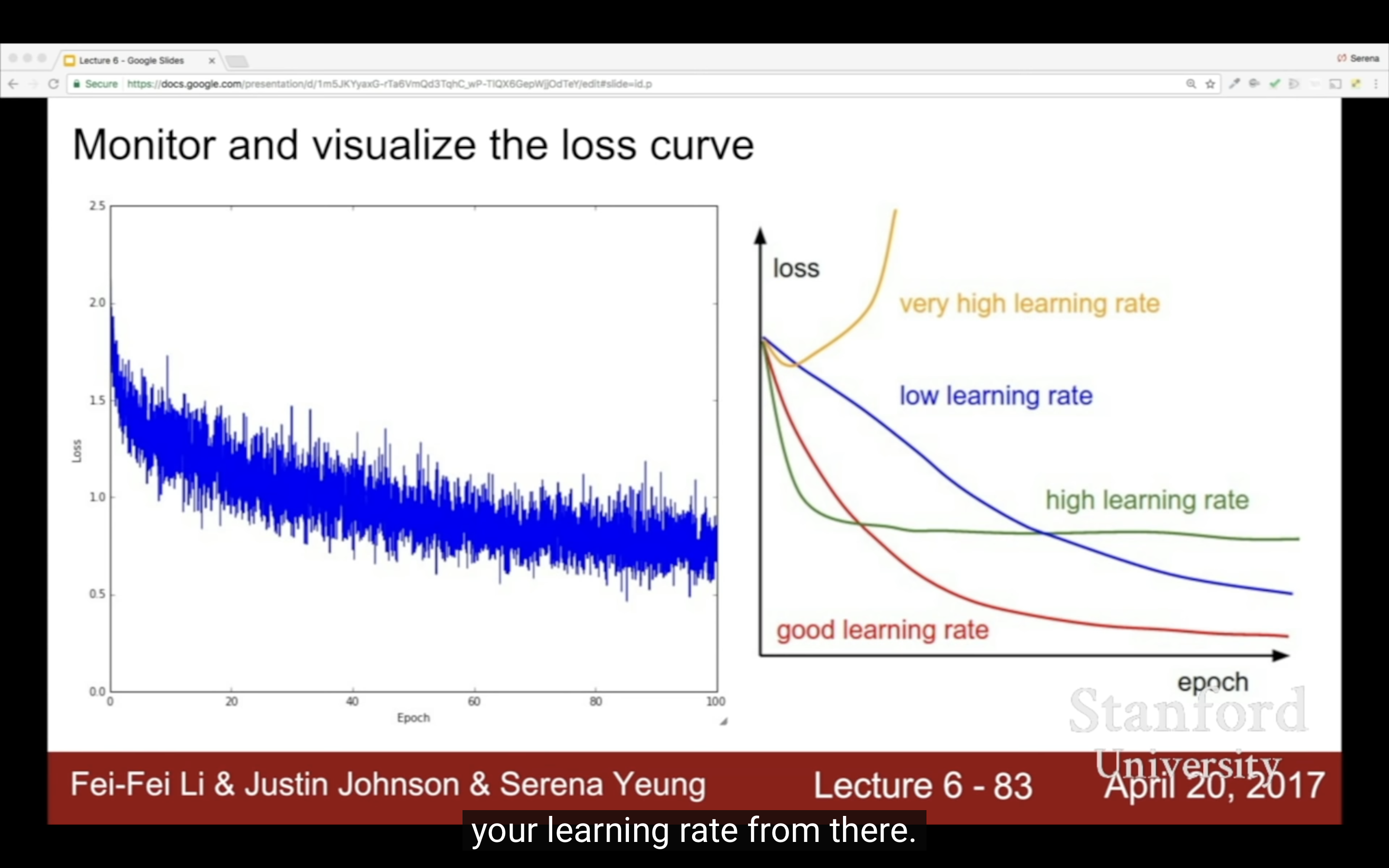 |
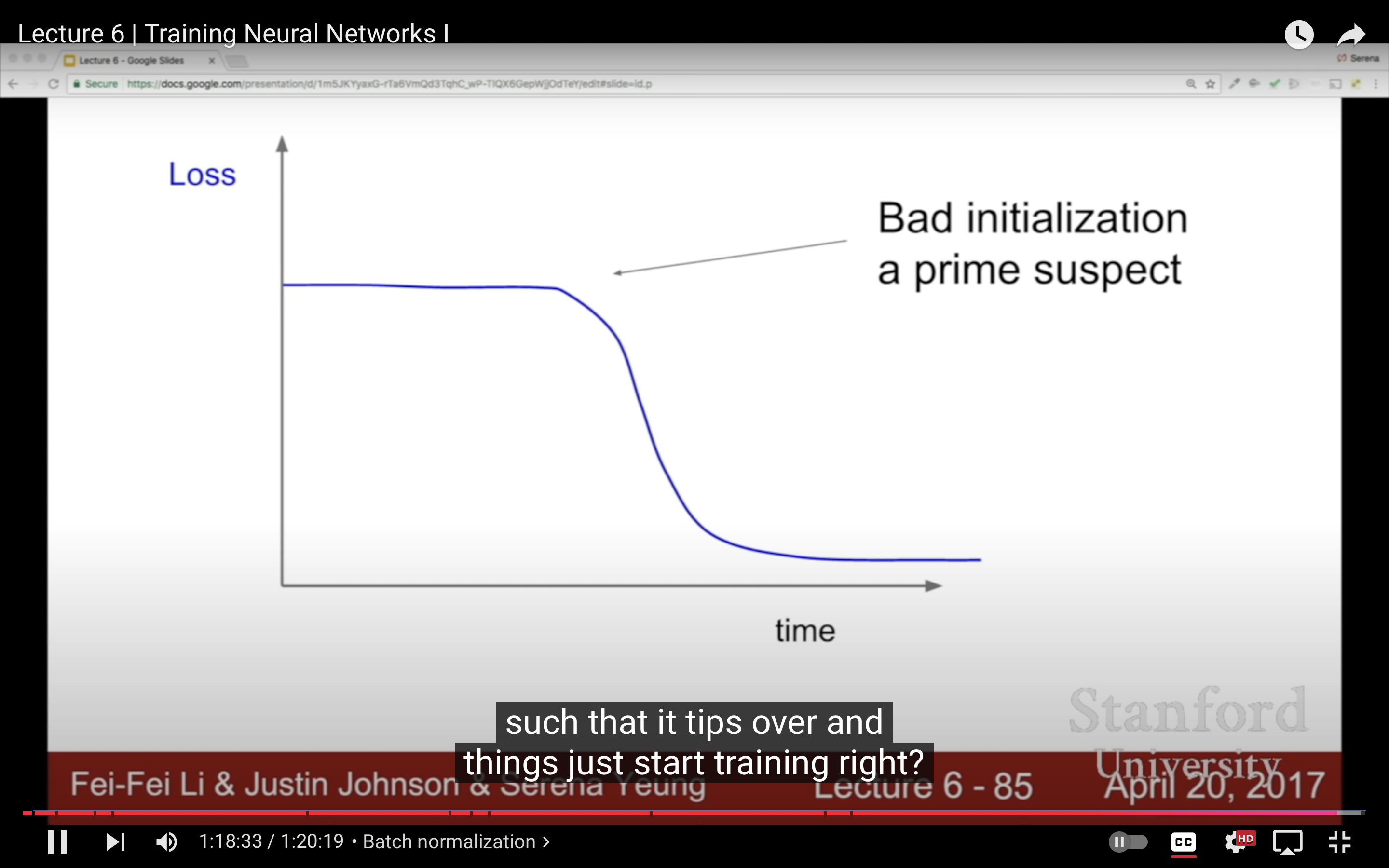 |
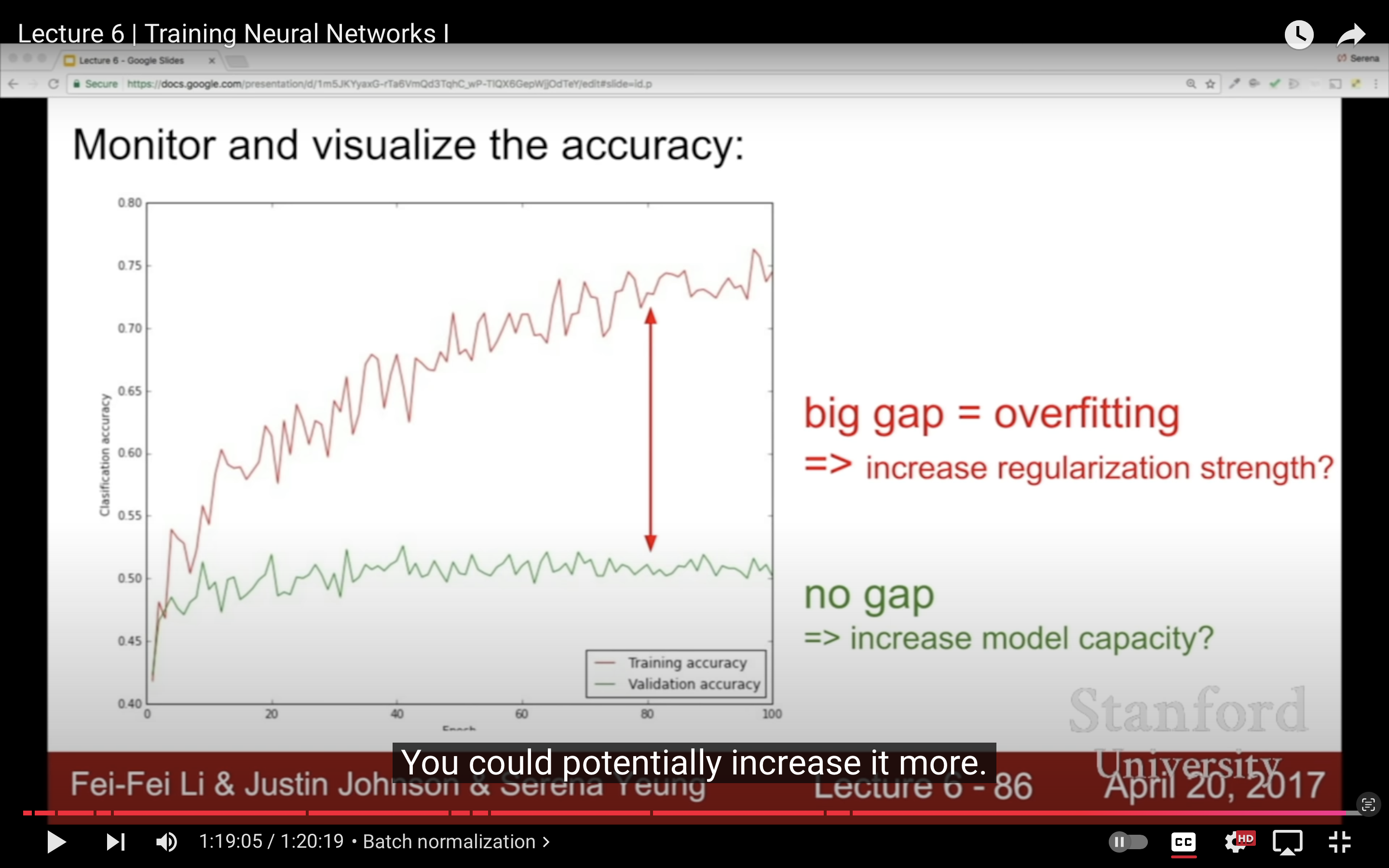 |
Track the ratio of weight updates / weight magnitudes
“Track the ratio of weight updates / weight magnitudes” 简单来说,指的是计算在每次训练迭代中,权重更新的大小与权重的当前大小之间的比例。
计算方式:
权重更新(Weight Updates):计算在一次迭代中,权重的更新量,通常表示为:
其中,$\eta$ 是学习率,$\nabla_w L(w)$ 是权重关于损失函数的梯度。
权重的大小(Weight Magnitudes):权重向量的模长,通常使用 L2 范数计算:
权重更新与权重大小的比率(Ratio of weight updates to weight magnitudes):
目的:
衡量更新幅度与权重大小的关系:这个比率可以反映梯度更新的幅度相对于权重当前大小的比例。
- 比率太大:可能表明学习率过高,导致梯度更新过大,容易导致训练不稳定。
- 比率太小:可能表明学习率过低,更新幅度过小,训练过程过于缓慢。
调节训练过程:通过监控这个比率,可以帮助调整学习率,以确保训练过程既不太剧烈,也不太缓慢,保持合理的收敛速度。
“Track the ratio of weight updates / weight magnitudes” 通过计算每次权重更新的大小与权重大小之间的比率,帮助评估训练是否稳定、学习率是否合适。
Lecture 7
改變了一個超參後,其他超參的最優值會改變嗎?比如改變model size,learning rate的最優解不太會變,如果已經找到一個較好的範圍了,就算最壞改變也只是讓模型更慢收斂到global optimal而已,尤其是用了比較好的optimization策略。
- Fancier optimization
- Regularization
- Transfer Learning(回想起2021年剛來,就瘋狂讓我學遷移學習,現在都沒人在提了)
Fancier optimization
注⚠️:公式裡的x實際上是w。
| local minima versus saddle point | |
|---|---|
 |
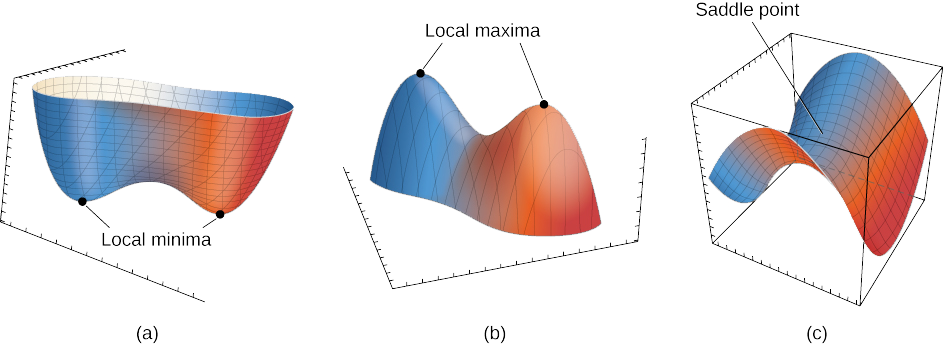 |
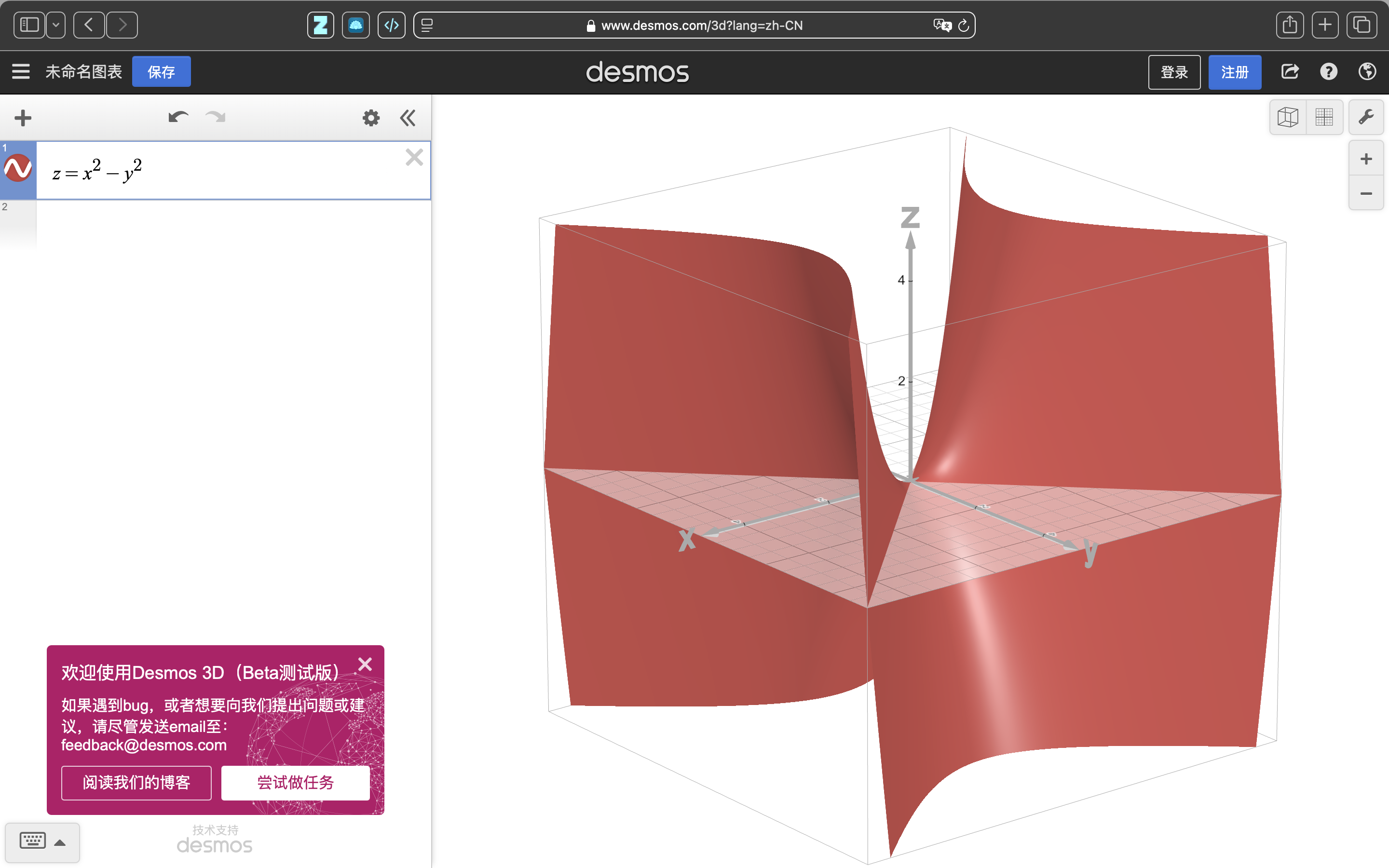
SGD Problems:
| 1.跟上面zig zag例子一樣,這個問題不光希望通過BN數據/特徵解決,也希望通過優化算法解決 | 2.local minima和saddle point,雖然一維看起來local minima比saddle point更嚴重,但比如說在100- dimension的空間裡,每一個方向都上升造成local minima是很罕見的(任何一個方向下降就不是local minima$f(x_0) \leq f(x), \quad \forall x \in 邻域U$),而且saddle point周圍斜率過低訓練過慢也是很麻煩的問題 |
|---|---|
 |
 |
3.因為mini-batch SGD每次只用一小部分,反應不了真實分佈,而且有很多噪音,所以訓練過程會很曲折meander,但其實full batch vanilla gradient descent還是有這些問題。
1. Momentum SGD
一些物理術語:
- velocity(速度,=speed速率+方向);
- Kinetic Energy(動能);$KE=\frac{1}{2}mv^2$
- Momentum(動量);p=mv,碰撞中的動量守恆:在兩物體碰撞過程中,雖然動能可能不守恆(如在非彈性碰撞中),但動量總是守恆的。
- Kinetic Friction(動摩擦);
- Static Friction(靜摩擦)。
動量和慣性的關係:
假設有兩個物體,質量分別為 1 kg 和 10 kg,兩者都以相同的速度 5 m/s 移動。
輕物體的動量:
重物體的動量:
儘管兩者的速度相同,但重物體的動量要比輕物體大,這意味著在相同的外力作用下,重物體的運動狀態更難改變,這就是慣性強的表現。

velocity一般就初始化為0。
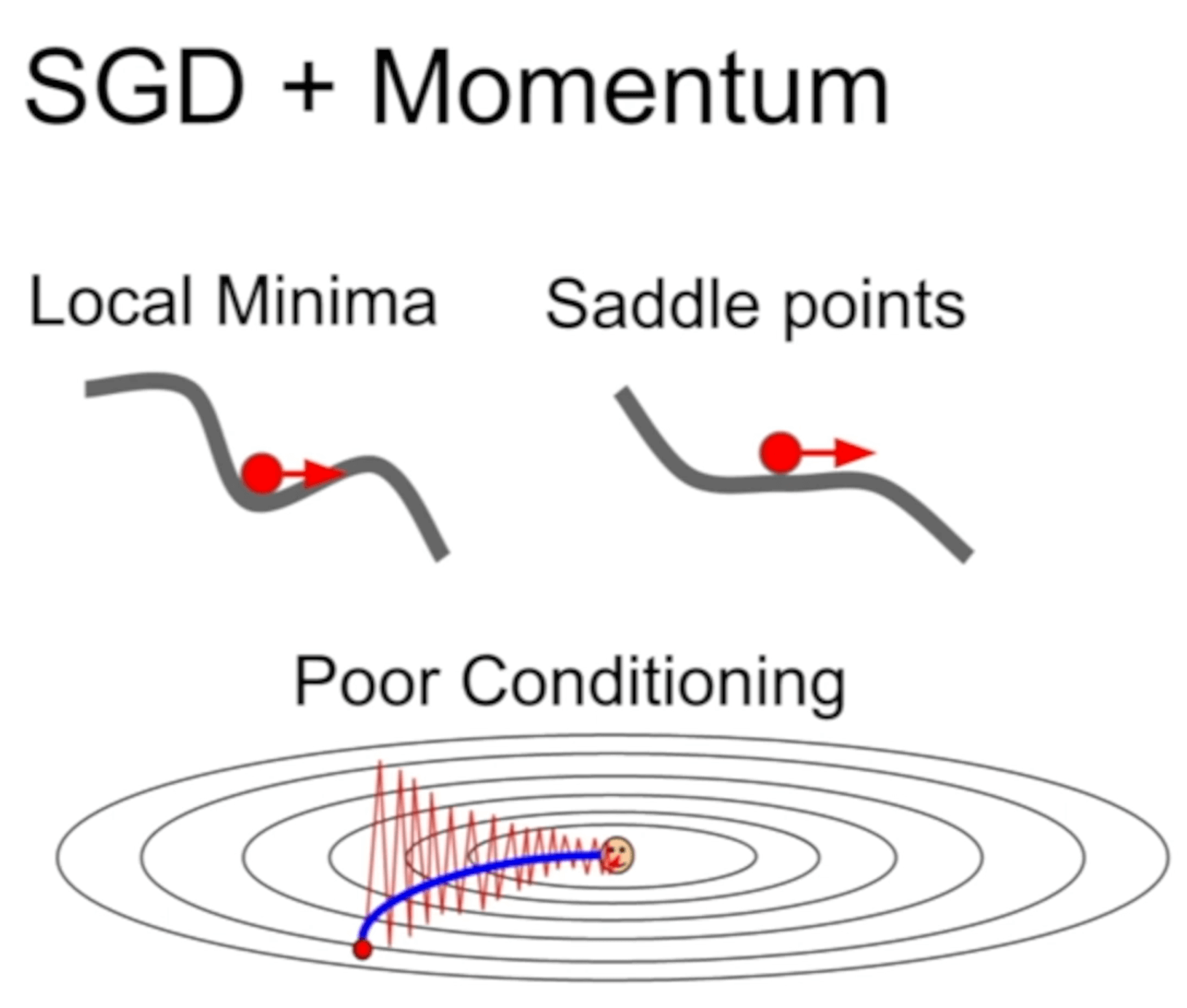
有個同學的問題問到了我的疑惑,如果因為這個動量,gradient衝過了一個narrow/sharp很窄的最優點怎麼辦?Justin Johnson的解釋是,我們還是希望要一個flat平台的最優點,更robust,就算很窄的那個是最優點,我們不一定想要。
2. Nesterov Momentum
上面稍微變體。
| 公式看著有點頭疼,其實就是永遠在更新完gradient的點上計算新gradient,而不是在更新前計算gradient。現在計算有問題,希望loss和gradient一起計算,於是有了下面的版本。 | |
|---|---|
 |
 |
3. Ada Grad
類似於每次除以之前所有gradients的總和,目的是為了平均過大和過小的斜率/變化率/梯度以解決上面的zig-zag問題,但導致每次的梯度更新會越來越少。
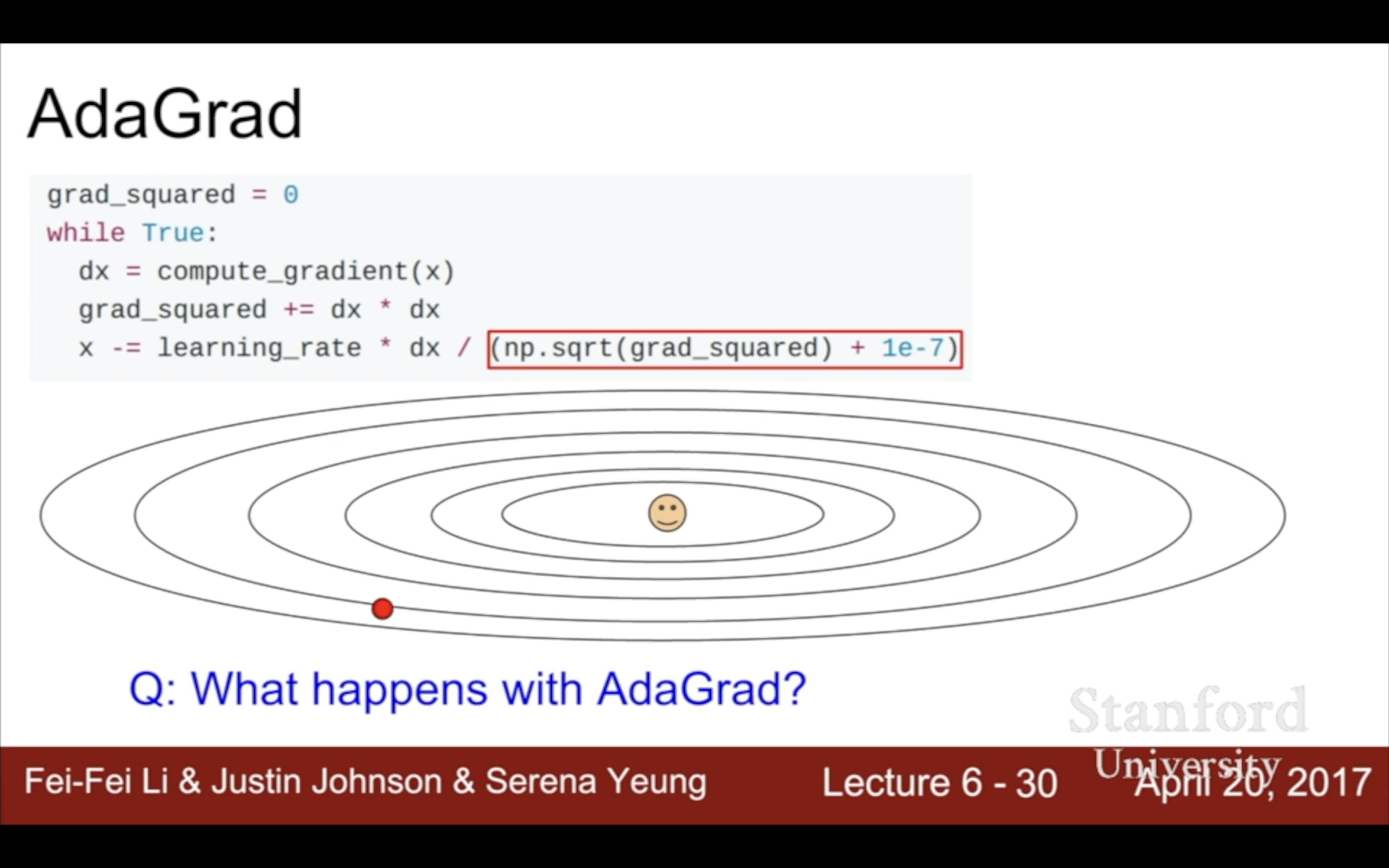
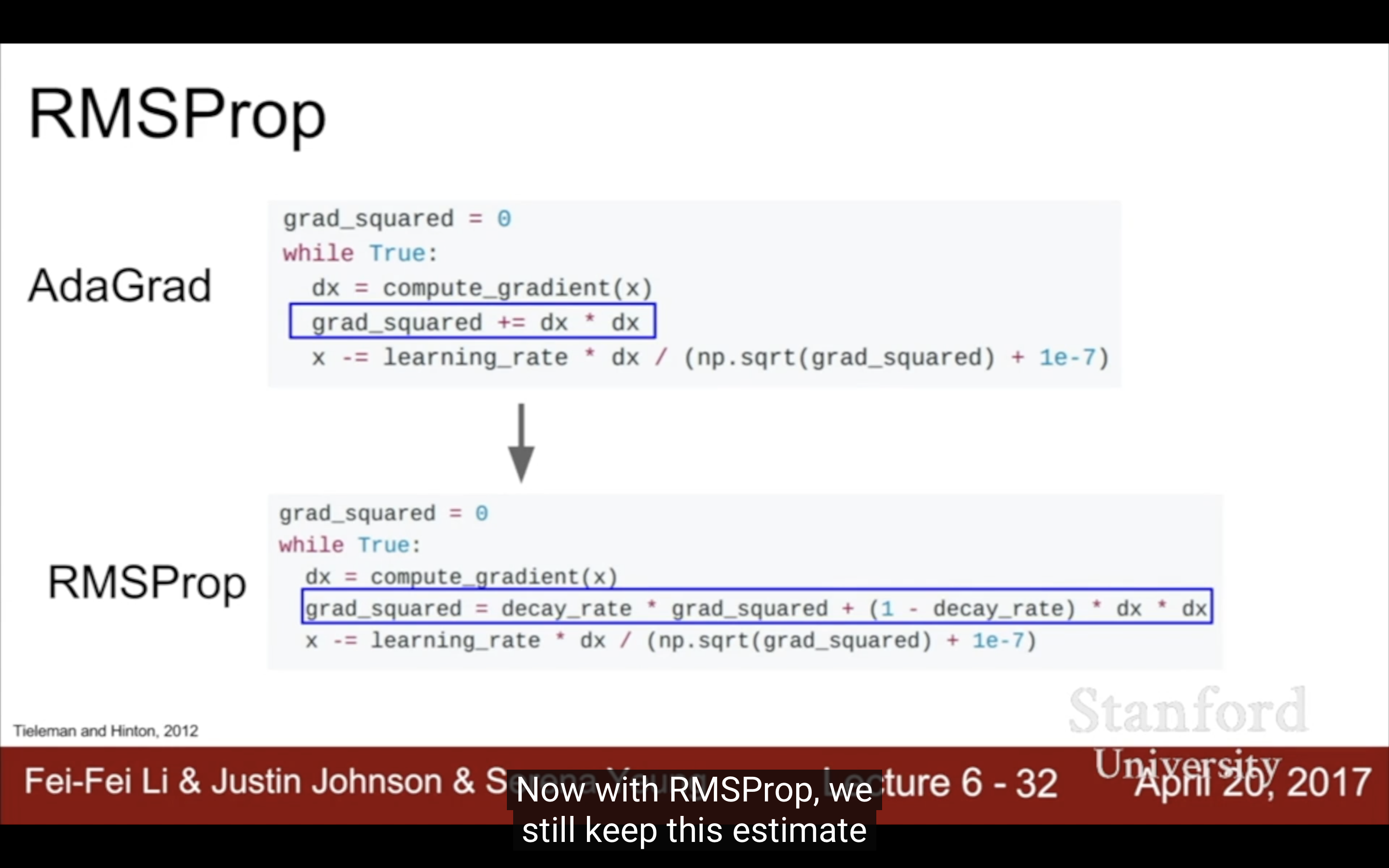
4. RMSProp
上面的slight variation,這個分母會自己變小。
5. Adam

所以剛開始更新的時候底下分母很小,如果first moment不幸也很小的話可能導致更新幅度很大,讓模型更難收斂。要知道這不是因為loss函數斜率很大,只是因為adam 特性。

6. Learning Rate
| decay over time | 一般SGD Momentum用lr decay,而且最好先選一個lr,再用cross-validation選一個好的decay |
|---|---|
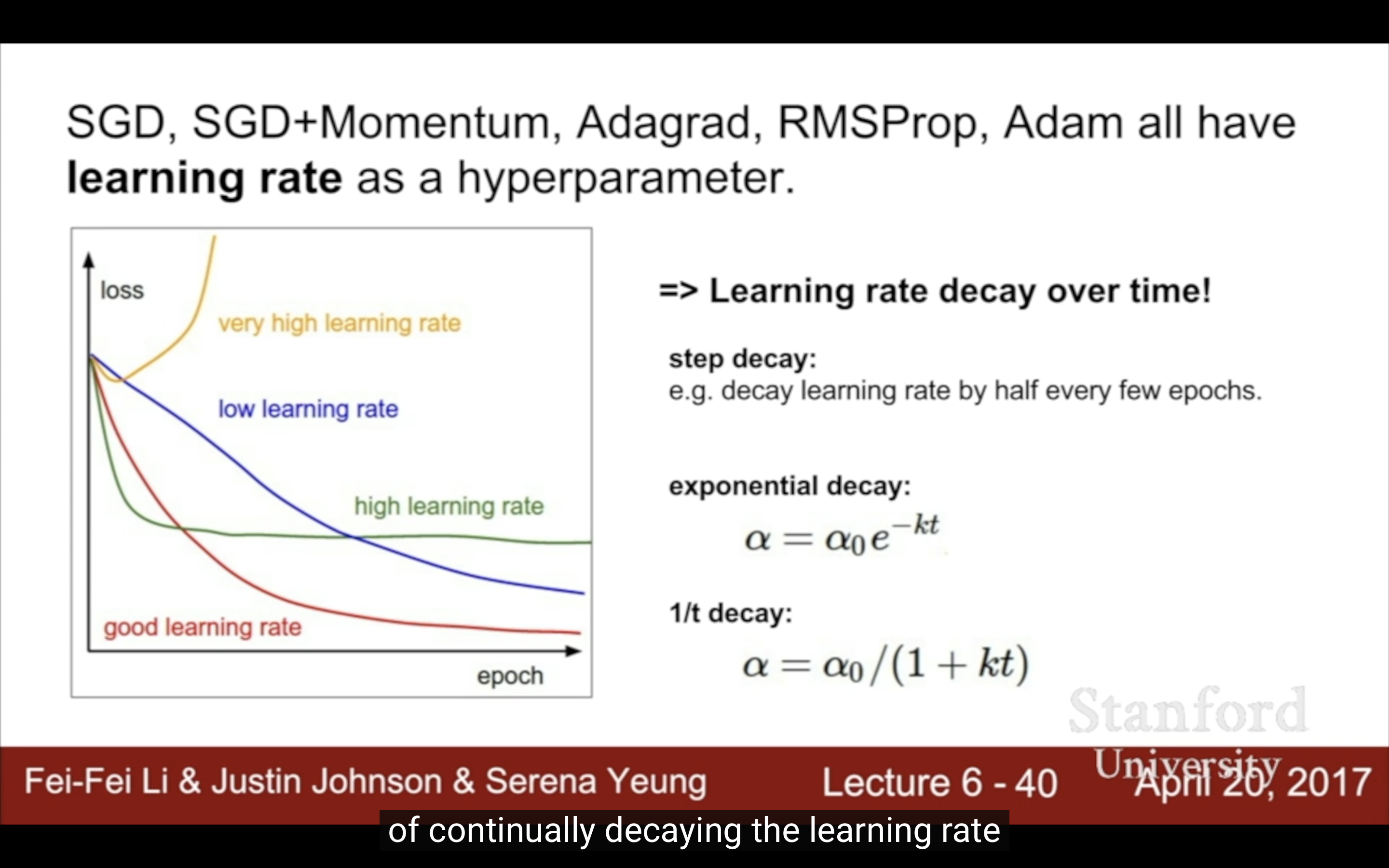 |
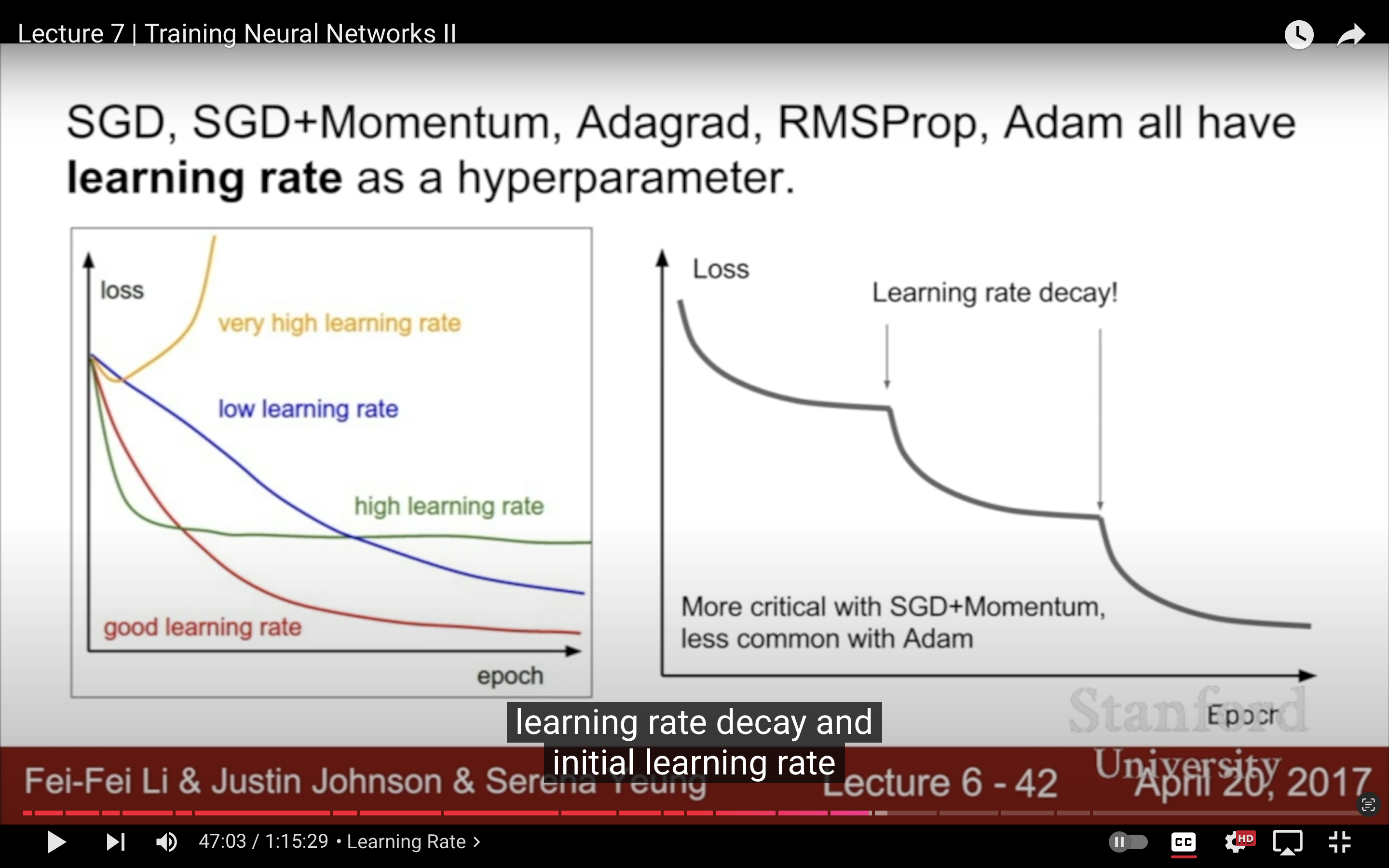 |
7. Second-order Optimization
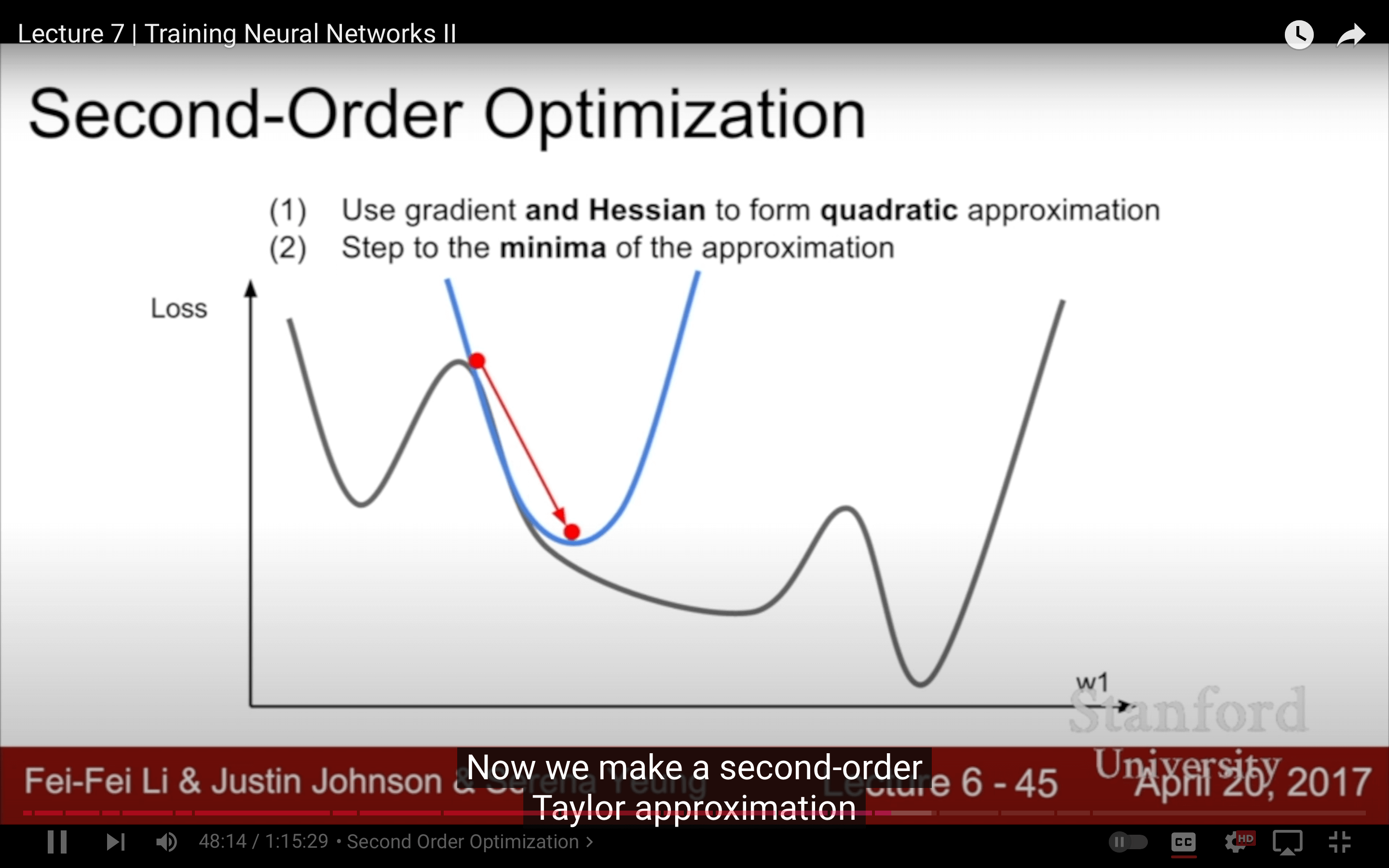
好像沒見有人用過,這個倒是可以拿來當畢業論文的創新點。XD
| 考慮拿來水論文 | |
|---|---|
 |
 |
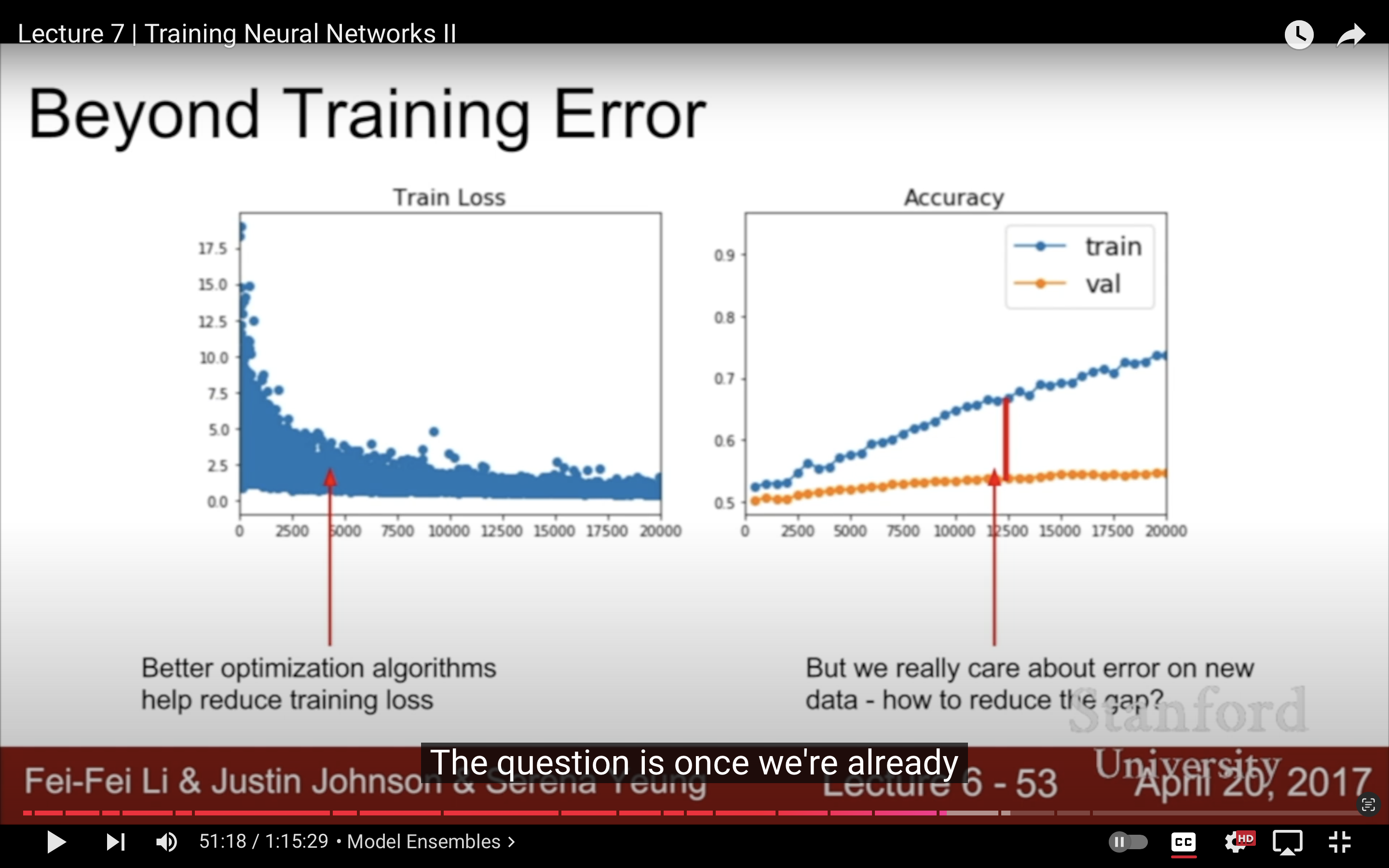
8. Test Error
| 如果在Training Dataset已經做得足夠好了,怎麼減小train error和test error之間的gap?記得嗎?test set是最後啟用的,我們只能用val set測試 | 用不同的隨機初始化訓練十個模型,平均他們的預測結果,在比賽裡還是有用的 | 或者可以在模型訓練的不同階段,把weights拿出來幾個snapshots當不同模型,自己跟不同時間的自己ensemble,2017當周的ICLR |
|---|---|---|
 |
 |
 |
ensemble的模型可以用不同的超參數。
如果不訓練多個模型來提升泛化能力,單模型改善表現可以使用正則。
Regularization
1. Dropout
在 dropout 技術中,將神經網絡中的一部分神經元的輸出設為 0,而不是將其輸入設為 0。
| 這種看起來就是totally messing with nets的行為怎麼就好用了? | |
|---|---|
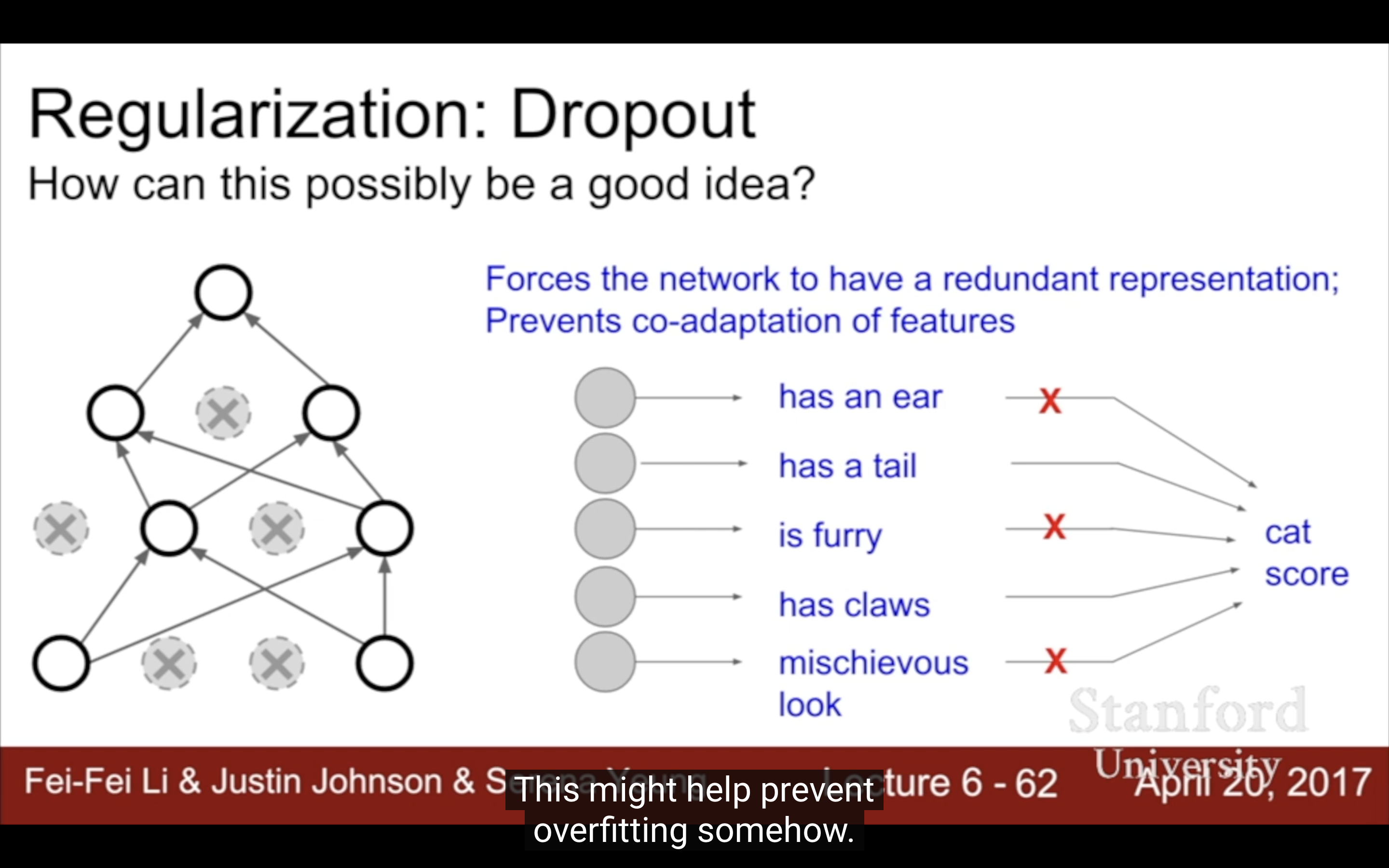 |
 |
反正就是好用。
| test做法 | ||
|---|---|---|
 |
 |
 |
dropout當然會導致training更久,因為w更新得更少了?
有點像都是引入了噪聲,有時bn就夠了,但dropout相當於給regularization加了個係數(變0的probability)更靈活了。
2. Data Augmentation
training加入stochasticity和noise的都可以看作regularization。
| pattern裡test time的marginalization是說“边缘化”,即再把噪聲給忽略掉 | 在網絡設計上加入這些“創新點”(別人的積木)可以當做大論文和專利的 |
|---|---|
 |
 |
每次用多少個正則手段?BN很多情況已經夠了(加速擬合、防止過擬合),應該每次感覺模型過擬合了才加入新的策略。
Transfer Learning
Off the shelf和off the wall到底啥意思?
这两个短语的含义是通过比喻或隐喻演变而来的,跟它们字面上的意思有些联系。让我分别解释一下为什么会有这样的意思:
Off the shelf
这个短语最初的字面意思是从货架上拿下来的物品。我们都知道商店里货架上的商品是直接可供购买的,顾客不需要等待生产或定制。所以,“off the shelf” 引申为“现成的”或“不需要定制的”。这个表达强调的是可以直接得到、无需额外处理的意思。例子:在一些领域,像软件、硬件、书籍等商品,有现成的商品直接从货架上取下,可以即刻使用,因此常常被形容为“off the shelf”。也可以用来描述任何“常规、标准化”的东西。
Off the wall
这个短语的起源比较有趣。它通常解释为某物“从墙上弹出来”,在字面上听起来像是某物离开了正常的轨迹,变得不受控制或不合常规。墙是一个常见的边界或框架,东西从墙上弹出来就意味着它突破了这个框架或界限。在这个意义上,“off the wall” 形容的是“跳脱框架、非常规、不拘一格”的事物。因此,原本它用来形容某事或某人行为怪异、出乎意料或充满创意,后来这个含义得到了广泛应用。
例子:如果你看到一个人的行为或想法非常独特,无法用传统的方式理解,或者说他的艺术作品完全不符合常见的审美标准,就可以用“off the wall” 来形容它的独特性或非常规性。
这些表达通常是从具体的、可观察的现象逐渐引申出更抽象的意义。
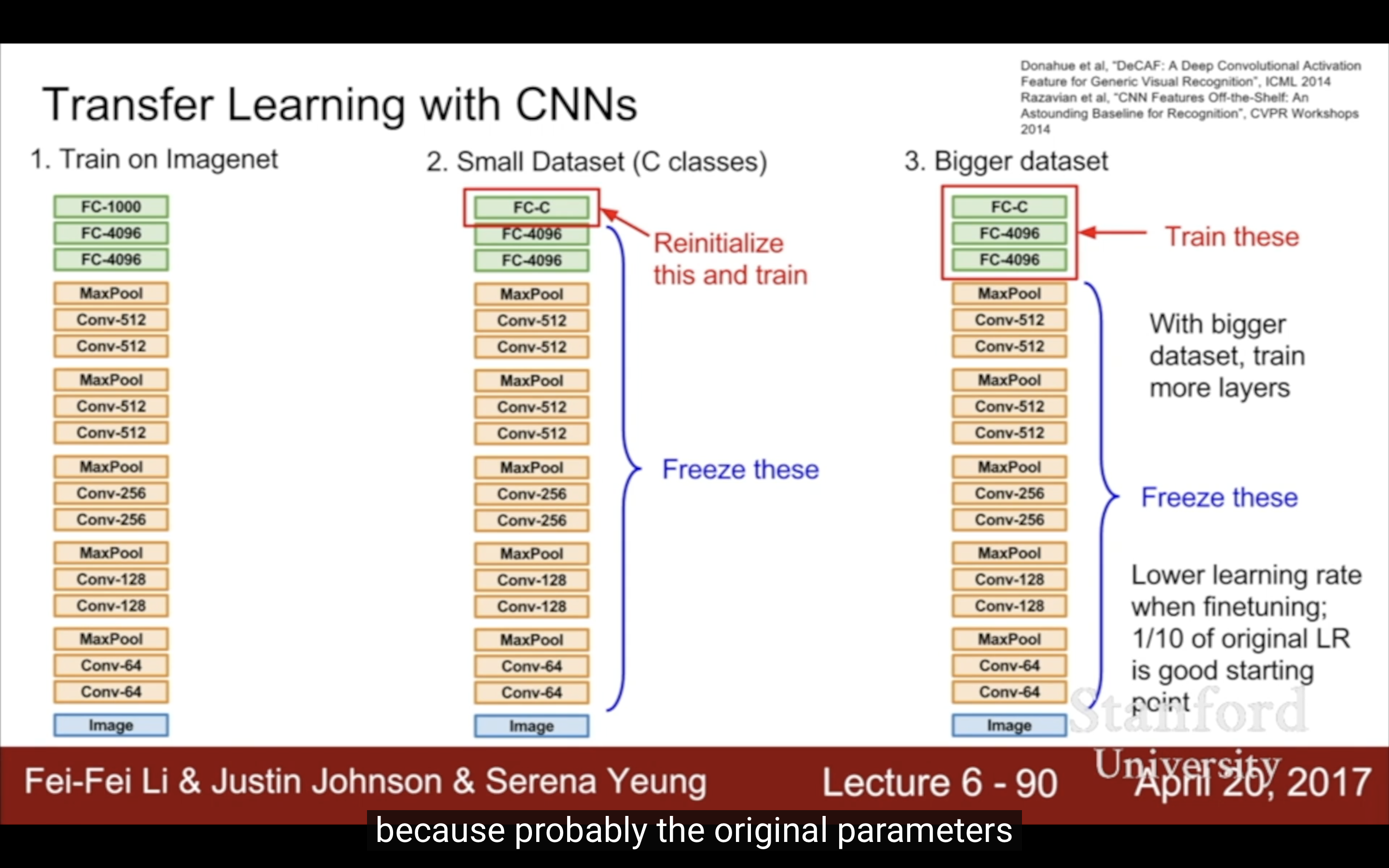
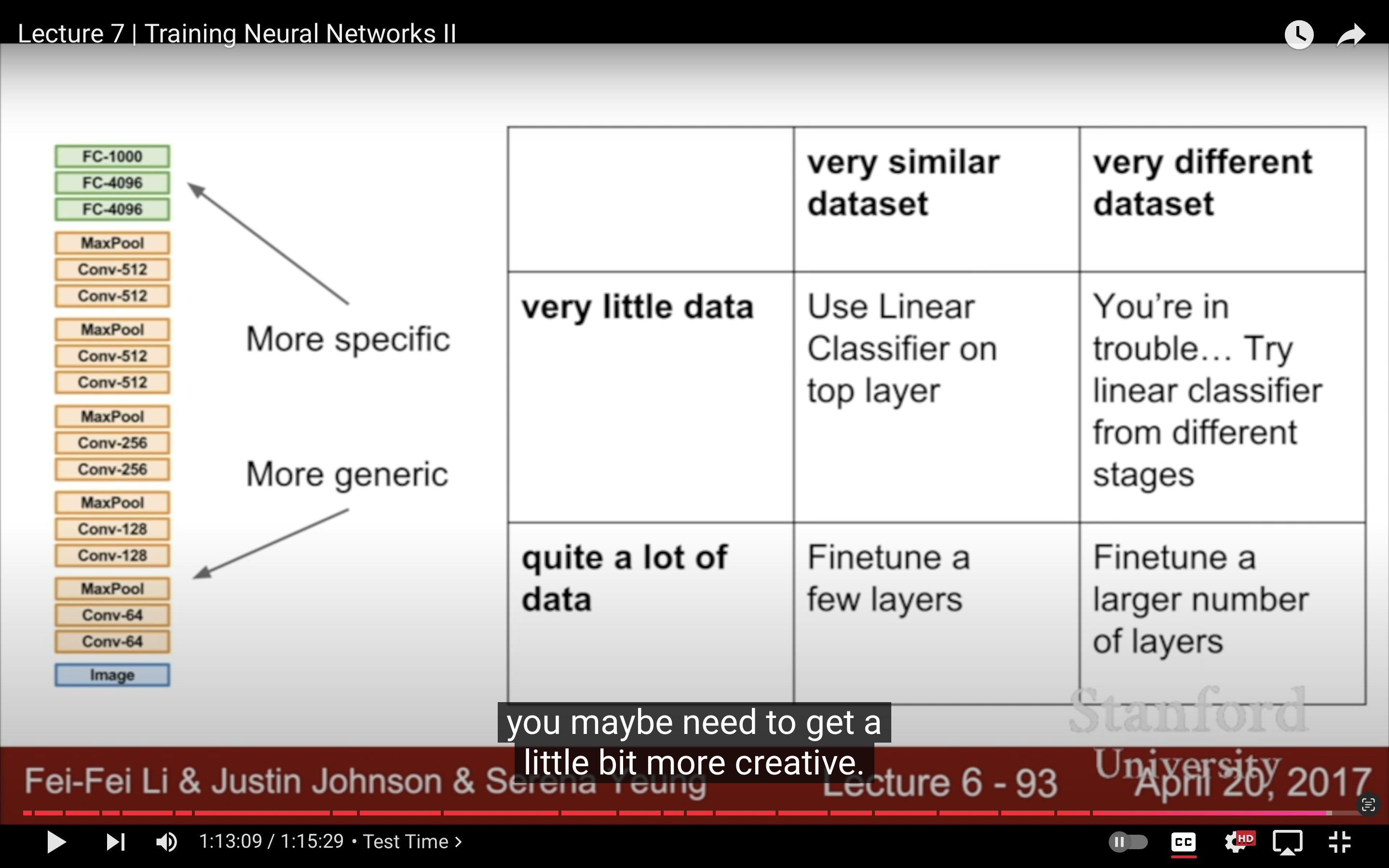
| 當時的CNN剛開始pretrain-finetune,已經不train from scratch了。 | |
|---|---|
 |
 |
optimization- training loss
regularization-test performance
transfer learning-less data
剛發現原來invisibility:true/false這個已經沒用了,得-BeInvisible,都給忘了。另外priority一定要有,不然推薦文章排序會bug。
Lecture 8
- CPU vs GPU
- Deep Learning Frameworks
- Caffe / Caffe2
- Theano / TensorFlow
- Torch / PyTorch
CPU vs GPU
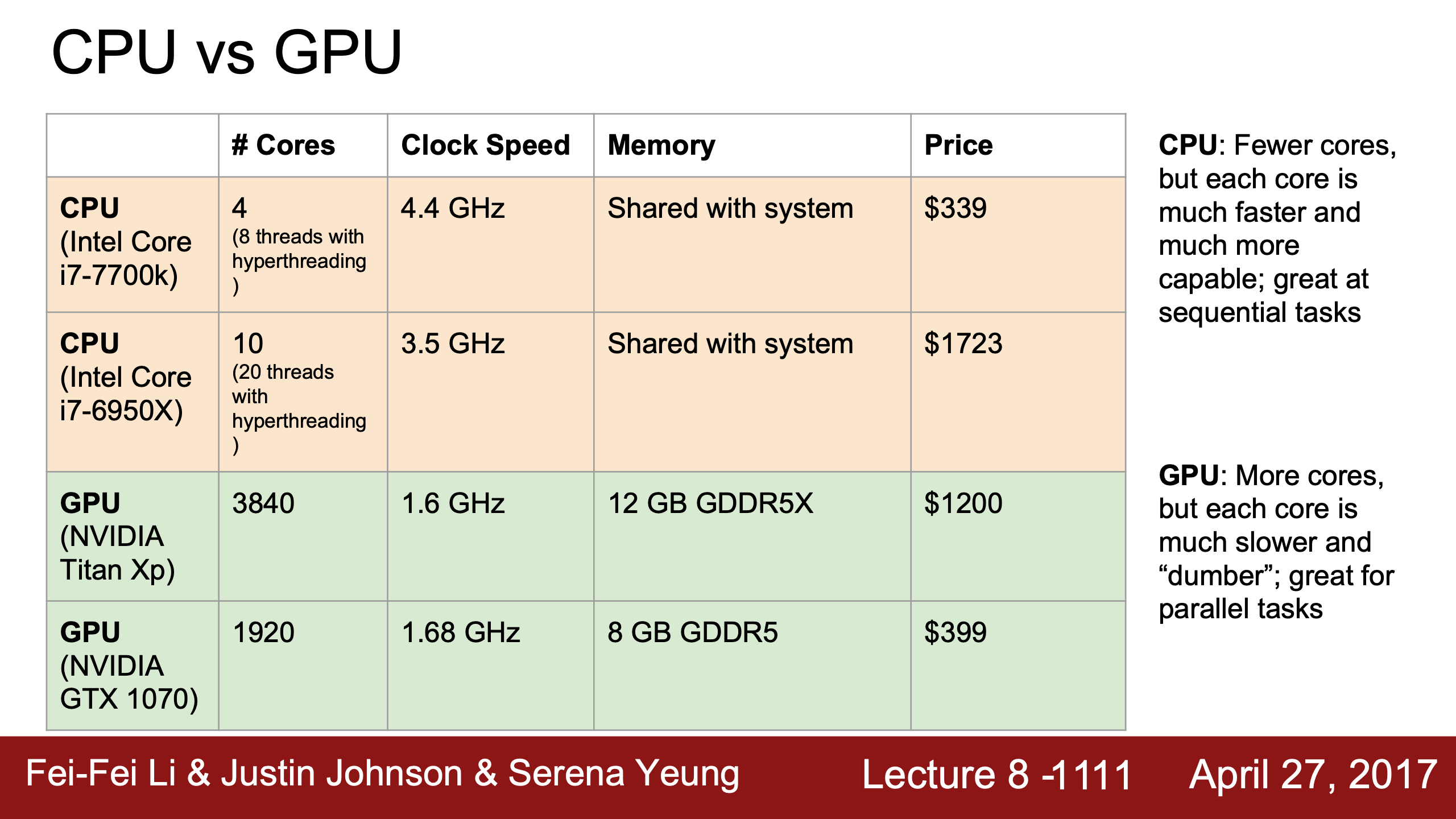
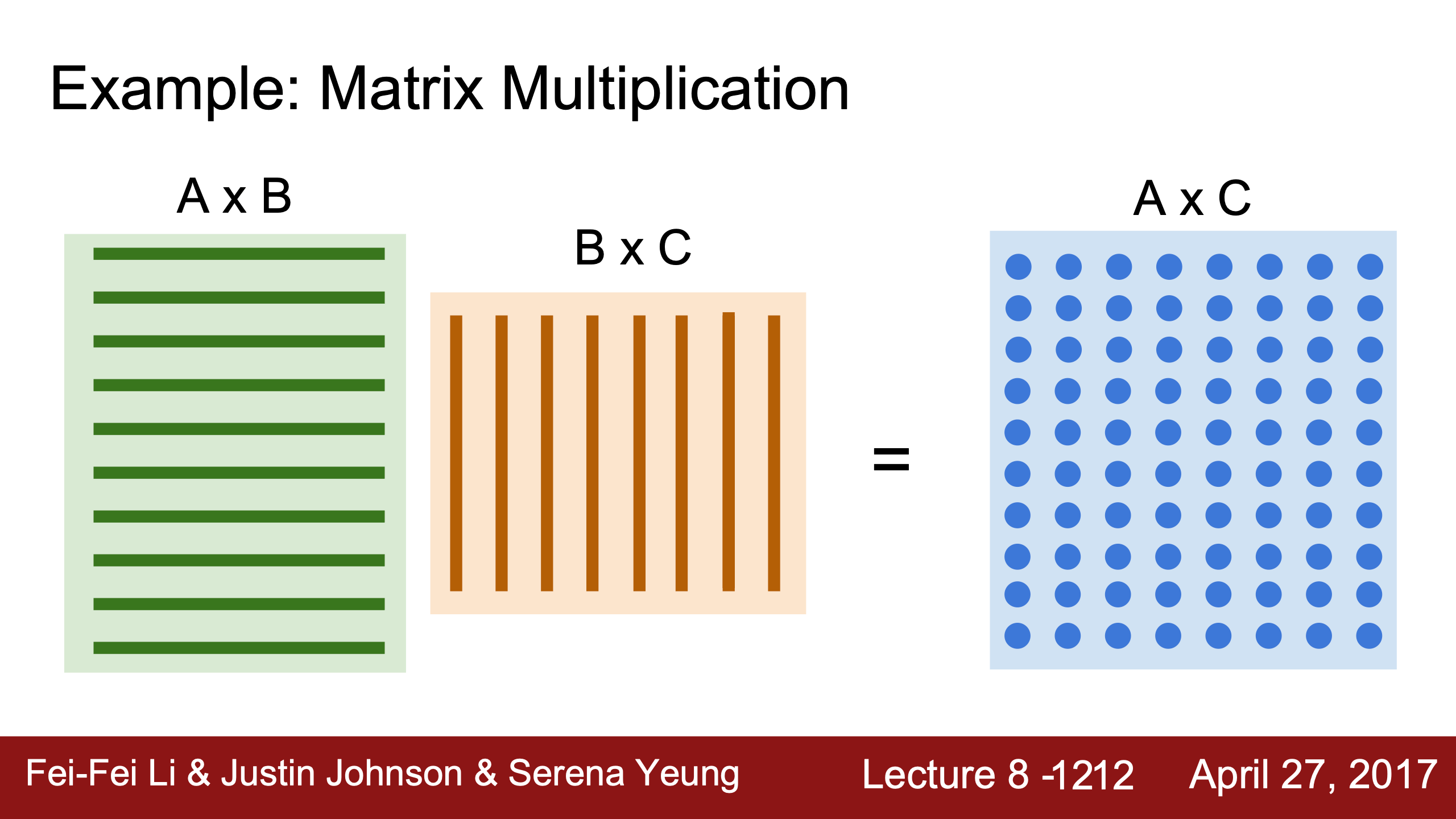
對應的行和列完全可以分別在不同的gpu core上同時運算,包括cnn的不同filter等都是parallelized任務

沒學會的cuda課,王麓涵好像是在做OpenCL系的矩陣算法優化來著,來浙大最遺憾的就是抄那門課作業糊弄及格(代碼之前又被我從郵件下回來了),在雲大最後悔的是編譯原理抄作業過關,有趣的是都是github上的校友repo,再其次就是OS課的大作業自己沒做出來抄了一段代碼。
Justin Johnson說是他從沒為自己的研究寫過cuda代碼。And cuDNN much faster than “unoptimized” CUDA.

Deep Learning Frameworks
Torch(NYU / Facebook)→PyTorch(Facebook),2017年時Justin Johnson最常用的就是Torch和Pytorch,現在也仍然是吧。
Caffe(UC Berkeley)→Caffe2(Facebook)
Theano(U Montreal)→TensorFlow(Google)
自己寫from scratch的(不是stretch伸展“Scratch”的原意是體育比賽地上畫的線)積木代碼雖然很爽,但是相比之下有三個不足:
The point of deep learning frameworks:
(1) Easily build big computational graphs
(2) Easily compute gradients in computational graphs
(3) Run it all efficiently on GPU (wrap cuNN, cuBLAS, etc)
無論是寫代碼效率還是運行效率都讓人不得不用第一代發源於academia第二代發展於industry的現成框架。
| Numpy is definitely CPU only. And it’s a pain to have to compute your own gradient. | GOAL: looks like numpy, but on GPU |
|---|---|
 |
 |
Tensorflow
沒有allocate memory,只是在graph裡加入這些nodes,所謂“placeholders”。
在CPU memory和GPU memory之間copy數據(weights/gradients)是開銷很大的,會成為bottleneck,定義成variable而不是placeholder可以避免這個問題:
Change w1 and w2 from placeholder (fed on each call) to Variable (persists in the graph between calls. Add assign operations to update w1 and w2 as part of the graph! Run graph once to initialize w1 and w2 first, then run many times to train.)
為什麼X和y不也放進graph裡?因為比如mini-batches裡的數據每個iteration會變,沒法提前存。
updates只是為了更新w加入的一個依賴於w的變量,因為想計算updates就要先更新前置w nodes,tf.group將多個操作聲明依賴關係,使他們作為一個整體運行,updates只是返回None。
相比一點一點group需要的參數,用tf的optimizer一兩行就夠了,內部實現跟上面一樣。
Justin Johnson也只知道placeholder是graph之外的,variable存在在graph裡面,並不清楚內部實現。
顯式定義的loss也可以用tf的函數代替。
最後可以把initial也都用簡便函數代替。除了這些還有很多高層庫能用,比如Keras就是基於tensorflow開發的(剛知道,也可以用tensorflow前身theano當後端),因為computational graph(比如ass1 ass2裡的)是很底層的實現,思考neural nets時一般會用比較高層的視角,用高層抽象的庫對開發效率是很有幫助的。在keras裡就變成了model.compile做back propagation(backward)工作,model.fit取代train()。Sklearn就不像keras是某個框架的API,也不是只面向深度學習的,是基於NumPy、SciPy 和 Cython的獨立机器学习库 。
前後對比:
| 代替前 | 代替後 |
|---|---|
 |
 |
Pytorch

相比tensorflow顯式更改cpu:0和gpu:0,pytorch是改數據類型——dtype = torch.FloatTensor。
 |
 |
torch沒有很多高層庫的選擇,只有nn.Modules。
tensorflow會先定義一個graph,然後train()時運行多次這個graph;而pytorch是每次前向forward pass裡都創造一個新的graph??這樣能讓代碼更clean。
Autograd

| 而且可以定義New Autograd Functions,就跟assignment1和2裡的layers/layer_utils一樣。 | optimizer.step()更新所有參數,tf裡是seesion.run() | 也可以Define new nnModules,跟assignment2裡classifier的fcnet和cnn非常相似。Define forward pass using child modules and autograd ops on Variables. No need to define backward - autograd will handle it. |
|---|---|---|
 |
 |
 |
torch.clamp(input, min=None, max=None, *, out=None)會把tensor(就是gpu上的np.array)最小值截斷到min,最大值截斷到max,不改變形狀。
dataloader是方便數據分割操作的玩意兒,需要定義自己的數據class,有minibatching, shuffling, multithreading等。例子等ass2寫的時候再理解吧
visdom Somewhat similar to TensorBoard: add logging to your code, then visualized in a browser Can’t visualize computational graph structure (yet?)(Justin Johnson沒用過)
Direct ancestor of PyTorch (they share a lot of C backend)
Written in Lua, not Python?我去居然是lua。2016年Justin Johnson上課還用torch,2017的pytorch是很新的東西。

static優勢是serialization序列化,部署時比較容易?
dynamic優勢:1.conditional,pytorch要做的跟我在numpy裡做過的一樣,但tf就要用tf.cond提前在graph裡加nodes/ops,倒是可以做到一樣的能力,就是麻煩;2.loop也是,循環也需要在graph裡顯式定義出nodes,可以看出tensorflow幾乎創造了自己的計算圖的programming language。Justin Johnson覺得學著用新語言很麻煩,用torch更舒適。
Recurrent networks 、Recursive networks,cs224n的Dynamic Graph Applications例子,比如對數Tree Data Structure的數據處理,torch可以就用普通的python做法,tensorflow就究極麻煩
Caffe
- Core written in C++
- Has Python and MATLAB bindings
- Good for training or finetuning feedforward classification models
- Often no need to write code!
- Not used as much in research anymore, still popular for deploying
Caffe: Training / Finetuning
No need to write code!
- Convert data (run a script)
- Define net (edit prototxt)
- Define solver (edit prototxt)
- Train (with pretrained weights) (run a script)
上這課的時候一個周前剛Facebook發布了caffe2。
- Static graphs, somewhat similar to TensorFlow
- Core written in C++
- Nice Python interface
- Can train model in Python, then serialize and deploy without Python
- Works on iOS / Android,
 |
 |
Lecture 9
Case Stydies:
- LeNet-5
- AlexNet (2012 ImageNet Large Scale Visual Recognition Challenge (ILSVRC) Winner)
- VGG (ILSVRC’14 2nd in classification, 1st in localization)
- GoogLeNet (ILSVRC’14 classification winner)
- ResNet (ILSVRC’15 winner,也在COCO’15數據集上的各比賽裡都明顯優於其他模型)
這些模型都是ILSVRC比賽的冠軍模型,空缺的2013年的ZFNet只是增加了AlexNet的參數量。
李飛飛的ImageNet只在2010年到2017年之間舉辦了這個ILSVRC比賽,因為2017年之後ImageNet分類任務的錯誤率太低,已經沒有再在這個任務上提升的必要了。
ILSVRC的成功促進了深度學習技術在計算機視覺領域的爆炸性發展,但隨著技術的進步和研究焦點的轉移,比賽完成了其歷史使命而逐漸退出舞台。
LeNet-5
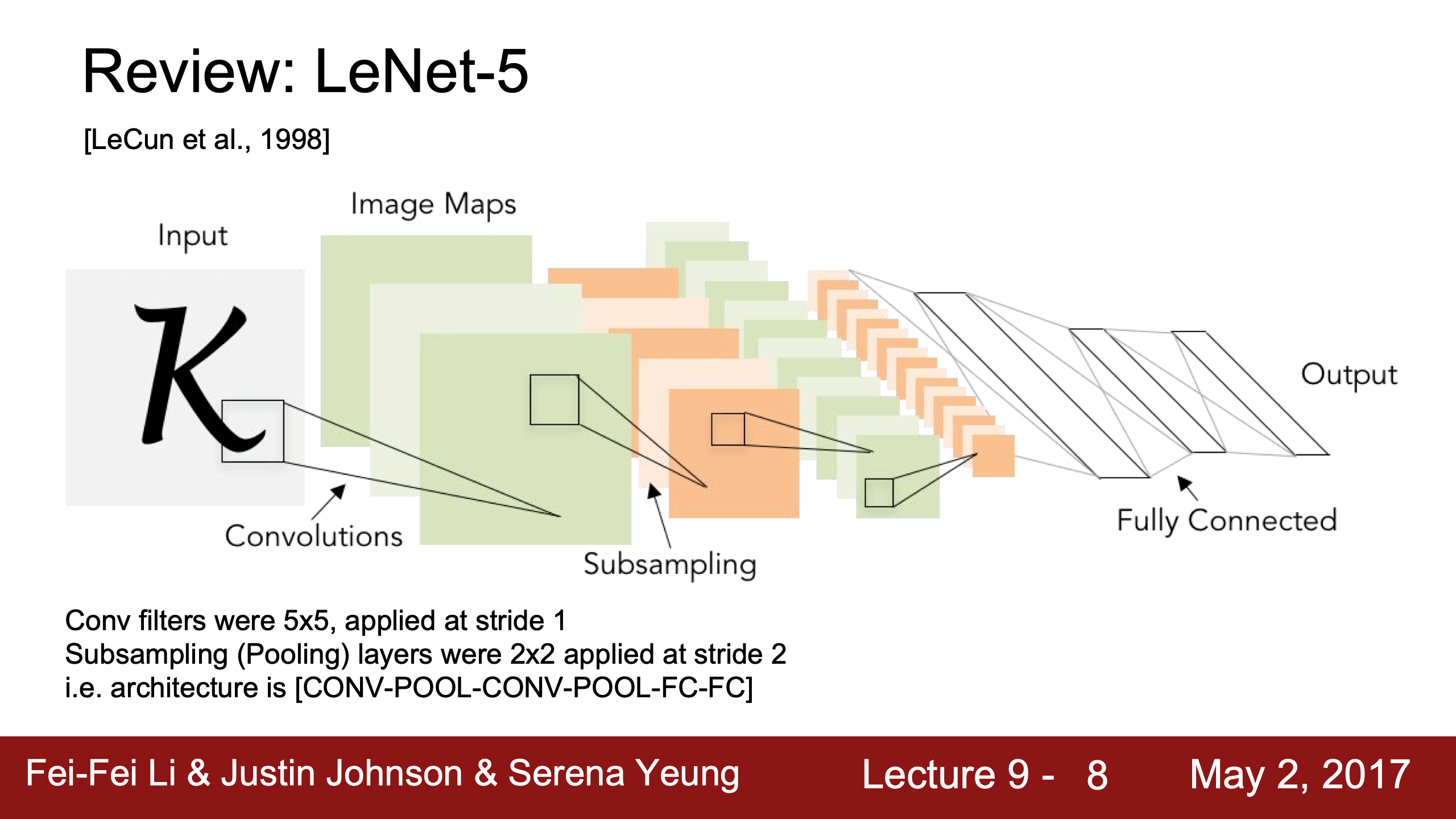
AlexNet
| 有些細節沒有說明(simplified),比如開始的224變成227(Serena說有些funny pattern) | 因為當時GTX 580顯存只有3G放不下所有參數,所以分成兩半訓練 |
|---|---|
 |
 |
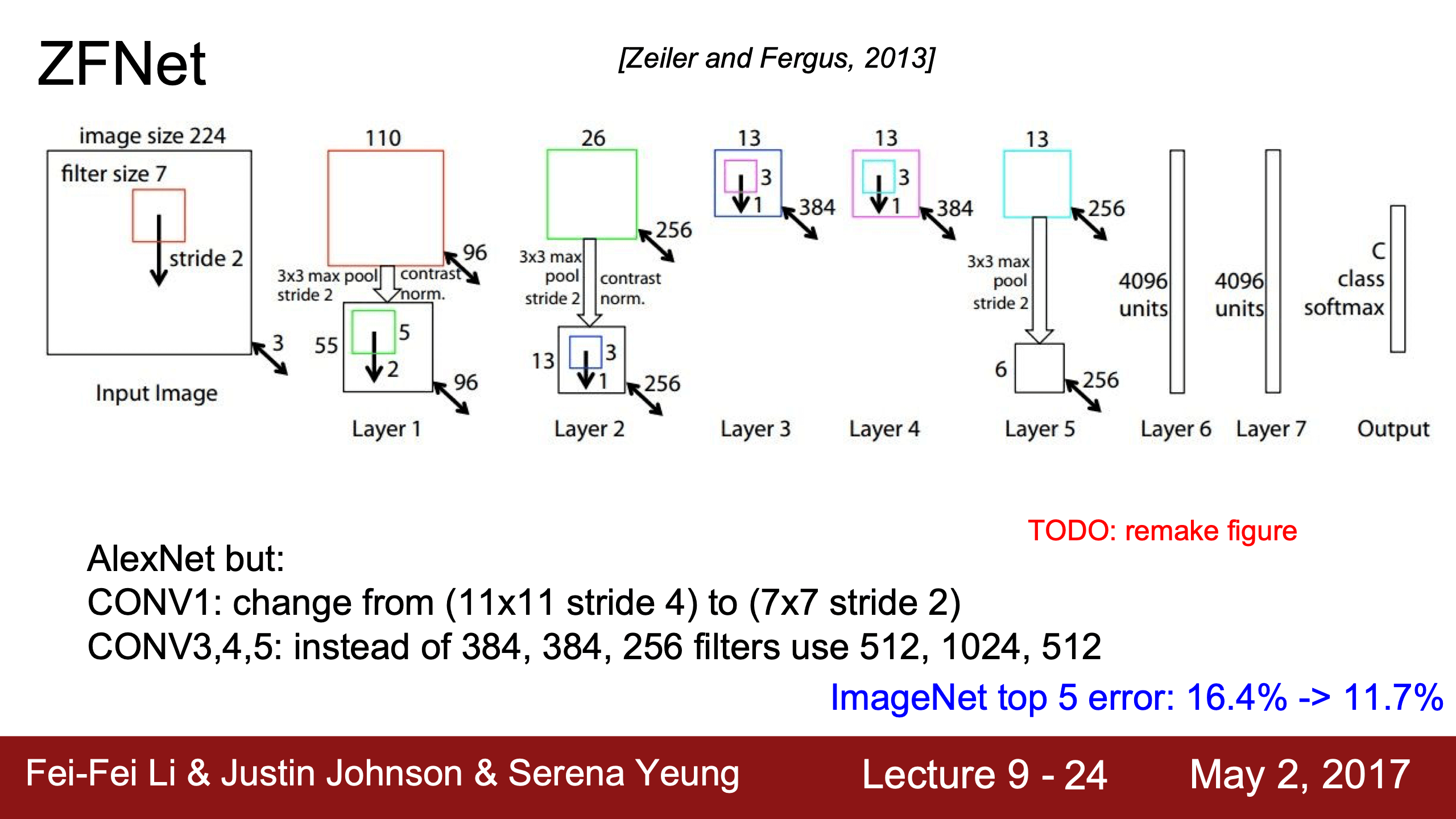
ZFNet
| 參數變了,但idea一致 | 之後就是filter變小,layers變多的趨勢 |
|---|---|
 |
 |
VGG
感受野(Receptive Field)指的是卷積神經網絡(CNN)中某個輸出單元對輸入圖像的感知範圍。簡單來說,它代表了輸出特徵圖上某個像素或神經元,能夠從原始輸入圖像中“看到”的區域大小。
感受野大小 就是這個像素值所受影響的輸入區域的範圍。例如:
如果感受野大小是 3×3,這意味著輸出特徵圖中某個像素對應於輸入圖像的 3×3 區域。
| 比如三層的activation maps裡,layer3上的一個點(一個像素)是由layer2的3x3範圍計算得到的,layer2的3x3是layer1上的5x5計算得到的。 | 因此7x7的一個filter可以由 3 個3x3的filter代替。所以從2014年的VGG之後都是上面所說的“filter變小,layers變多的趨勢”。 |
|---|---|
 |
 |
$3 * 3^2C^2 = 27C^2 < 7^2C^2 = 49C^2$,3 個 3x3 filters代替 7x7 filters,這個替換的參數量是原來的55%。
| 不是所有參數都要一直保存在顯存裡,梯度是圖裡Total Memory的2倍,無論是Hidden Layer/Activation Map還是Weights/Filters都是以浮點數存儲,FP32(32位浮點數,4字節) | VGG-16就是加FC一共16層,VGG-19多3層CONV,圖裡不知為何跟實際不太一樣,vgg應該是block1和block2有2層conv,vgg16後面3個blocks都是3層conv,vgg19後面3個blocks都是4層conv。 |
|---|---|
 |
 |
再詳細記錄一下數量計算,這個很有用:
- 存在顯存裡的數據:
- 模型參數Weights and Biases,每次前向和反向傳播都要用到;
- 梯度Gradients,反向傳播結束後可以釋放,前向完再佔用顯存;
- 激活值Activations(數據集dataset是在CPU Memory或磁盤裡),
- 哪些層有激活層?卷積層(Conv Layers),全連接層(FC Layers),所以這些層計算梯度需要考慮activation function;
- 哪些層沒有?批量歸一化層(BatchNorm Layers),Dropout之類的;
- 哪些激活函數需要存激活值?
- $\text{Sigmoid:} \quad \sigma’(x) = \sigma(x) \cdot (1 - \sigma(x))$
- $\text{Tanh:} \quad \frac{\partial \tanh(x)}{\partial x} = 1 - \tanh^2(x)$
- 哪些不需要存激活值,需要存激活函數的輸入而不是輸出,或者存別的?
- ReLU可以存activation的inputs而不是ouputs,或只存一個mask,輸入是正數的梯度是dout * 1,負數或0的梯度是dout * 0,這很像池化層(Pooling Layers),也是dout * MASK;
- Leaky ReLU/PReLU也差不多,只需要存一個MASK,區別是負數或0的梯度是dout * alpha;
- 除了ReLU/dropout這種存個MASK可以節省顯存之外,還可以用反向重計算(Recompute Activations)
- 如果顯存非常有限,可以在反向傳播時重新計算前向傳播的激活值,而不是在顯存中保存它們。這叫 梯度檢查點(Gradient Checkpointing),以計算時間換取存儲空間。
- 顯存使用 = 參數+激活數據+參數梯度(+激活梯度)
- 前向顯存 = 參數 + 激活數據
- 反向顯存 = 參數 + 激活數據 + 參數梯度
- 激活梯度包括$dx$和prelu裡的$d\alpha$,后者幾乎可以忽略,dx不需要存儲,因為它是逐層即時計算並傳遞的。
- 兩倍關係:反向傳播的顯存需求 = 正向傳播需求 + 參數梯度需求,大約是兩倍,在transformer這種參數量一定大於激活數據的模型裡,反向對正向是大於兩倍關係的。
- 混合精度訓練(Mixed Precision Training): 使用 16-bit 浮點數(FP16)存儲激活數據和梯度,顯著減少Memory占用;
- 模型壓縮: 减少参数数量,通过剪枝等方法减少存储需求。改數據類型也可以用在參數上,能成倍減少開銷。
- 上面的Weights and Biases、Activations、Gradients都是以浮點數存儲,一般是FP32(32位浮點數,4字節),即實際佔用顯存量就是數據量 x 4bytes。
為什麼用Softmax沒人用SVM loss?因為就是效果好。
- 模型集成提分:Use ensembles for best results
- FC7學到的特徵可以用於其他任務:FC7 features generalize well to other tasks
GoogLeNet
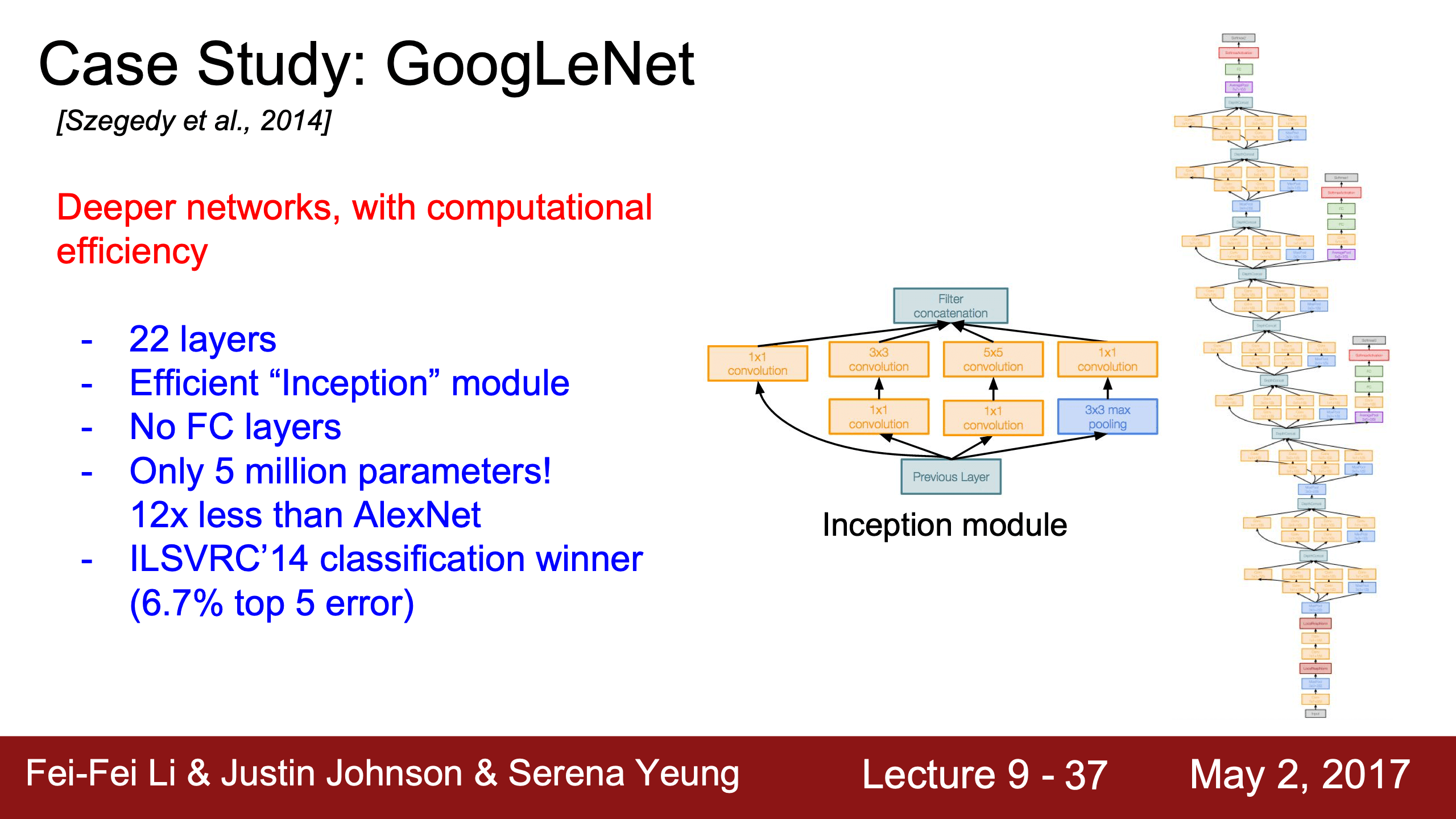
| 這裡通過padding強行讓output size都是28x28,而且pooling意味著下一個inception module的輸出只會更深層,開銷爆炸。 | 用1x1的conv減depth雖然會有一點information loss但是能降低超多開銷。 其他dimensionality reduction也是可以用的。 |
|---|---|
 |
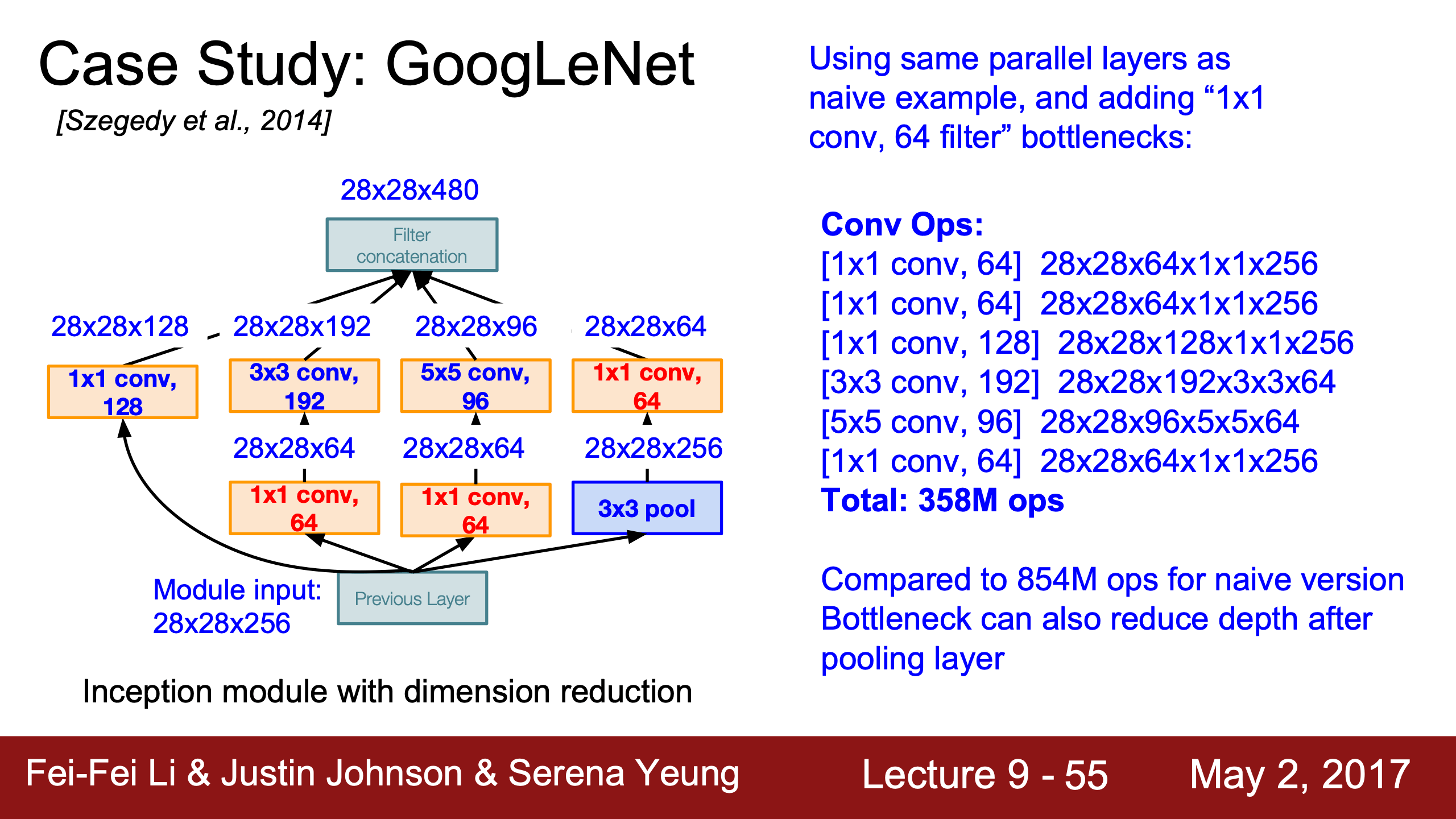 |
前面加兩個fc-loss(auxiliary outputs,training時3個loss不是分多次的只會有一次back prop,Serena也忘了inference時是三個loss取平均還是只用其中一個),更多地算前幾層梯度更新前幾層的參數,說是有更好的效果,說是有時梯度信息會在超長網絡裡丟失,這樣也可以緩解問題。
ResNet
何恺明閃亮登場。
既然趨勢是網絡越深效果越好,那可以直接狂堆層數嗎?這樣做其實會讓效果變差。而且是training/test error都高,所以並不是過擬合導致的。
一種假設是網絡越深越難優化,不然深層模型至少應該跟淺層一樣好,因為只需要copy淺層剩下的層讓input和ouput一致就行了。
那麼就讓模型學x的residual(x的殘餘),模型完全可以把f(x)學成0達到上面說的效果,也許這樣會更簡單一點。
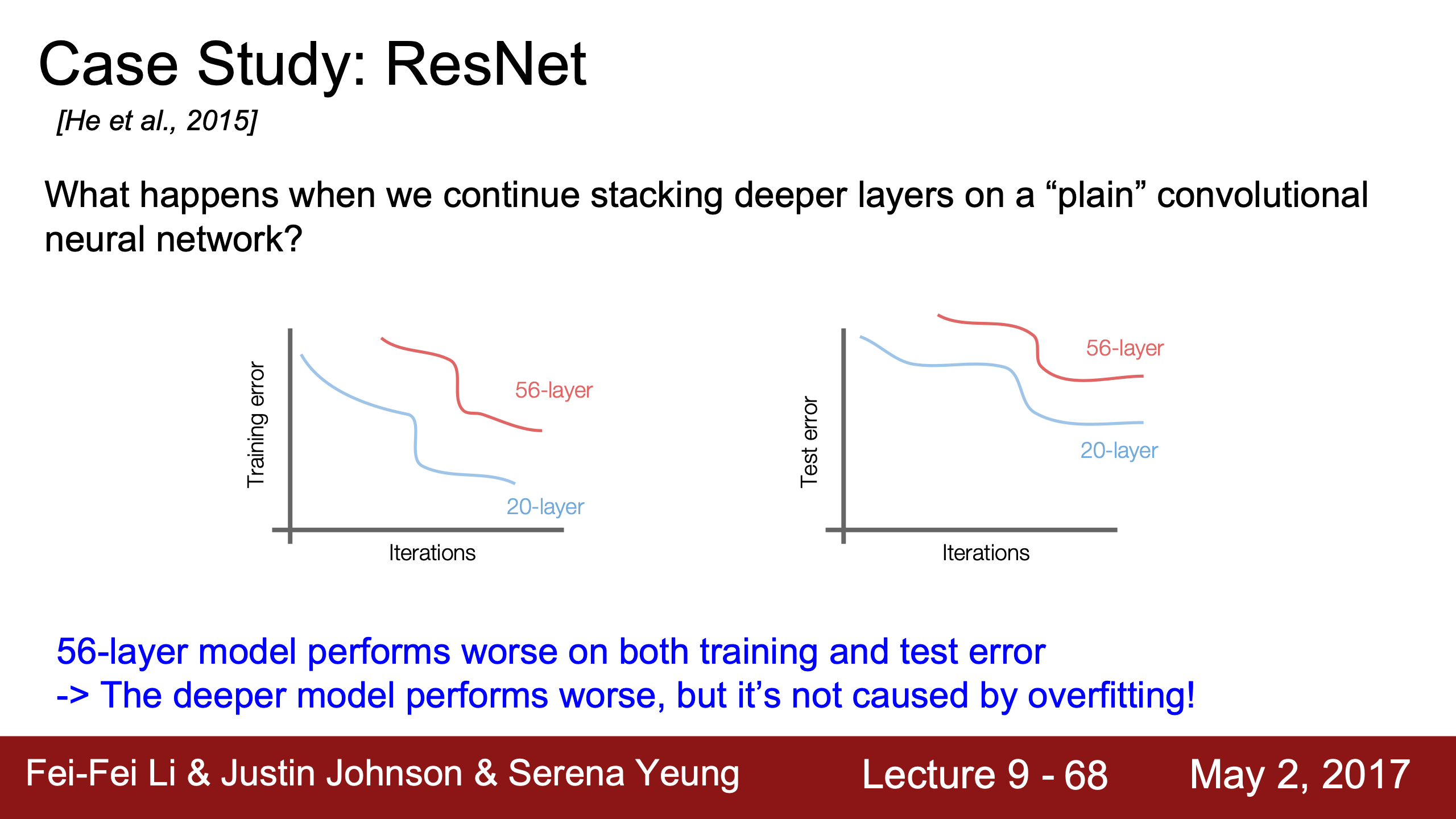 |
 |
實現細節:
| 丟掉VGG的兩層FC之後,參數量大大減少,記得上面VGG那裡計算參數量時幾乎全部都來自FC | 跟GoogLeNet一樣可以用1x1的conv減少channel depth | |
|---|---|---|
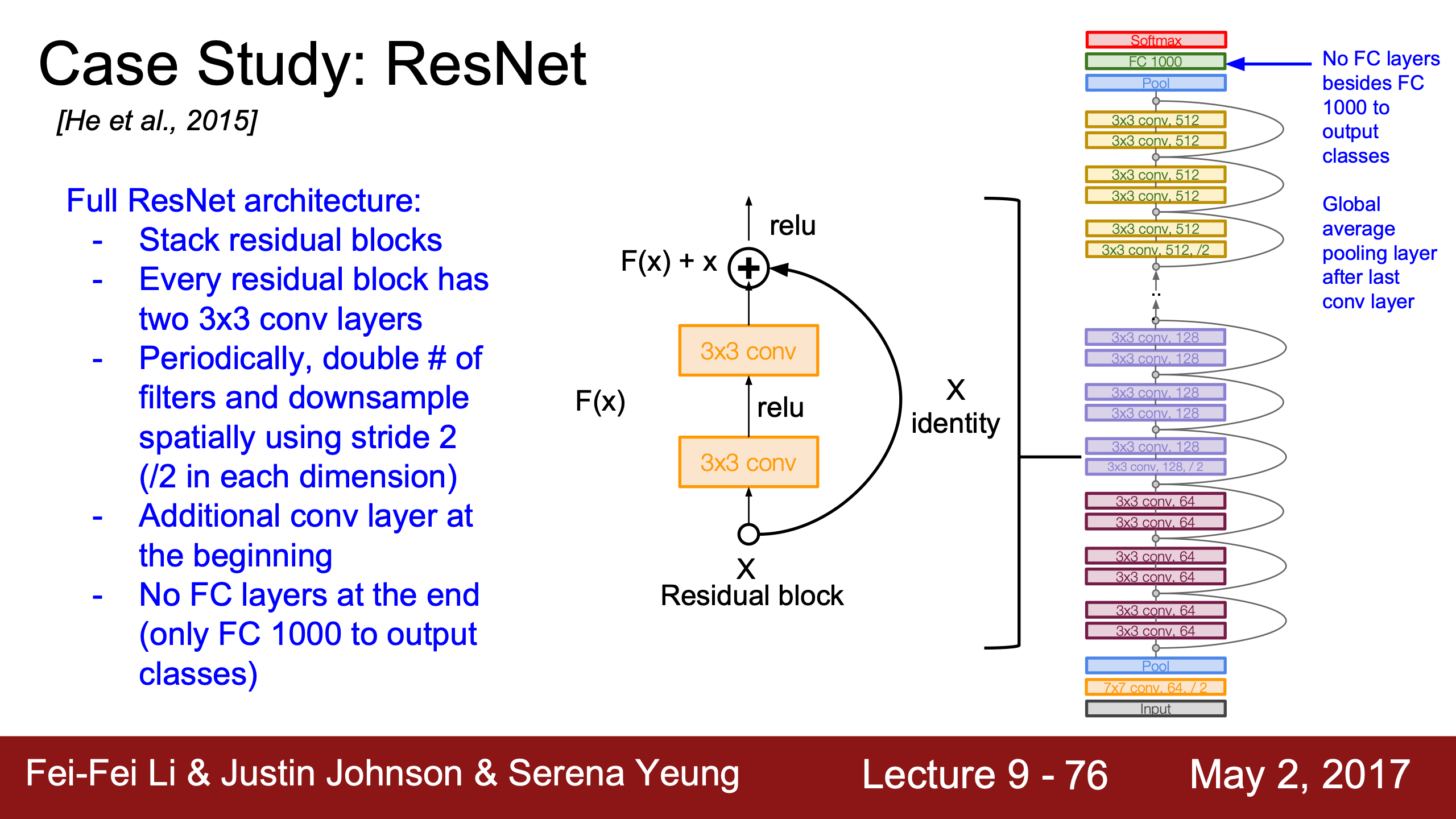 |
 |
 |
H(x) = f(x) + x裡,f(x) 和 x 的concatenation如果維度不同就無法逐元素相加,所以:
1. 維度本來一致時
如果 $x$ 和 $f(x)$ 的通道數和空間尺寸一致,直接相加即可:
- 條件:$x$ 和 $f(x)$ 的形狀為 $[N, C, H, W]$,其中 $N$ 是 batch size,$C$ 是通道數,$H$ 和 $W$ 是特徵圖的高和寬。
2. 通道數不一致時
當 $f(x)$ 改變了通道數時,需要對 $x$ 進行通道數匹配。
解決方法:使用 $1 \times 1$ 卷積進行投影,將 $x$ 的通道數從 $C_{\text{in}}$ 變換為 $C_{\text{out}}$:
- $W_{\text{proj}}$ 是 $1 \times 1$ 卷積核。
- $x’$ 和 $f(x)$ 的形狀一致。
3. 空間尺寸不一致時
當步幅 $s > 1$ 導致 $f(x)$ 的空間尺寸縮小(例如從 $[H, W]$ 變為 $[H/s, W/s]$),需要對 $x$ 進行下採樣。
解決方法:使用帶步幅 $s$ 的 $1 \times 1$ 卷積,同時調整通道數和空間尺寸:
- $x’$ 的形狀與 $f(x)$ 保持一致。
總之都是用 1x1 的conv修改維度。
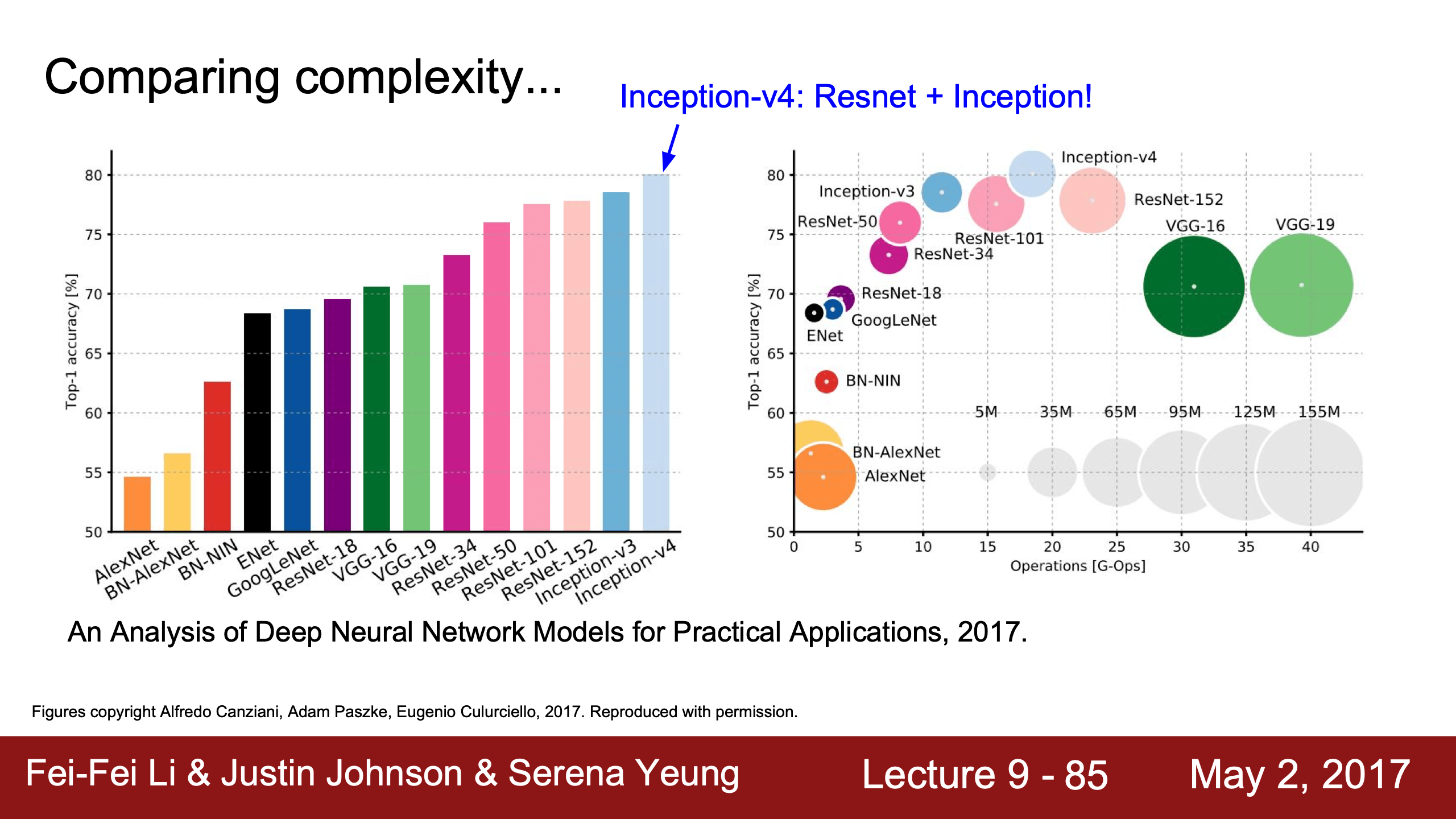
Other Architectures
- Network in Network (NiN)
- DenseNet,原來是中國人做的,根據這個solution試試看吧。
- SqueezeNet
沒細看,又開始急了,趕緊RNN。
MLP(Multi-Layer Perceptron) = 多層 FC 層(Fully Connected Layer) + 激活函數 + 正則。
Lecture 10
JJ為什麼說AlexNet是9層?chatgpt:
AlexNet 是一個經典的卷積神經網絡,最初提出時被認為是 8 層深,但有時也被描述為 9 層。這取決於如何計算層的數量。總層數 = 卷積層(5 層)+ 全連接層(3 層)+ Softmax概率輸出層(有時算有時不算)。
2014年還沒出BN,所以VGG和GoogleNet訓練得很吃力,不太能收斂。VGG是先訓練了個11層的,後續往裡加成16/19層,JJ說GoogLeNet的兩個ugly hacks只是用來幫助收斂的。
residual也會讓梯度更好反向傳播,因為有一條x的直通路線,完全不用擔心梯度消失(爆炸還是會的吧?)。
管理梯度流在任何模型裡都很重要,包括RNN。
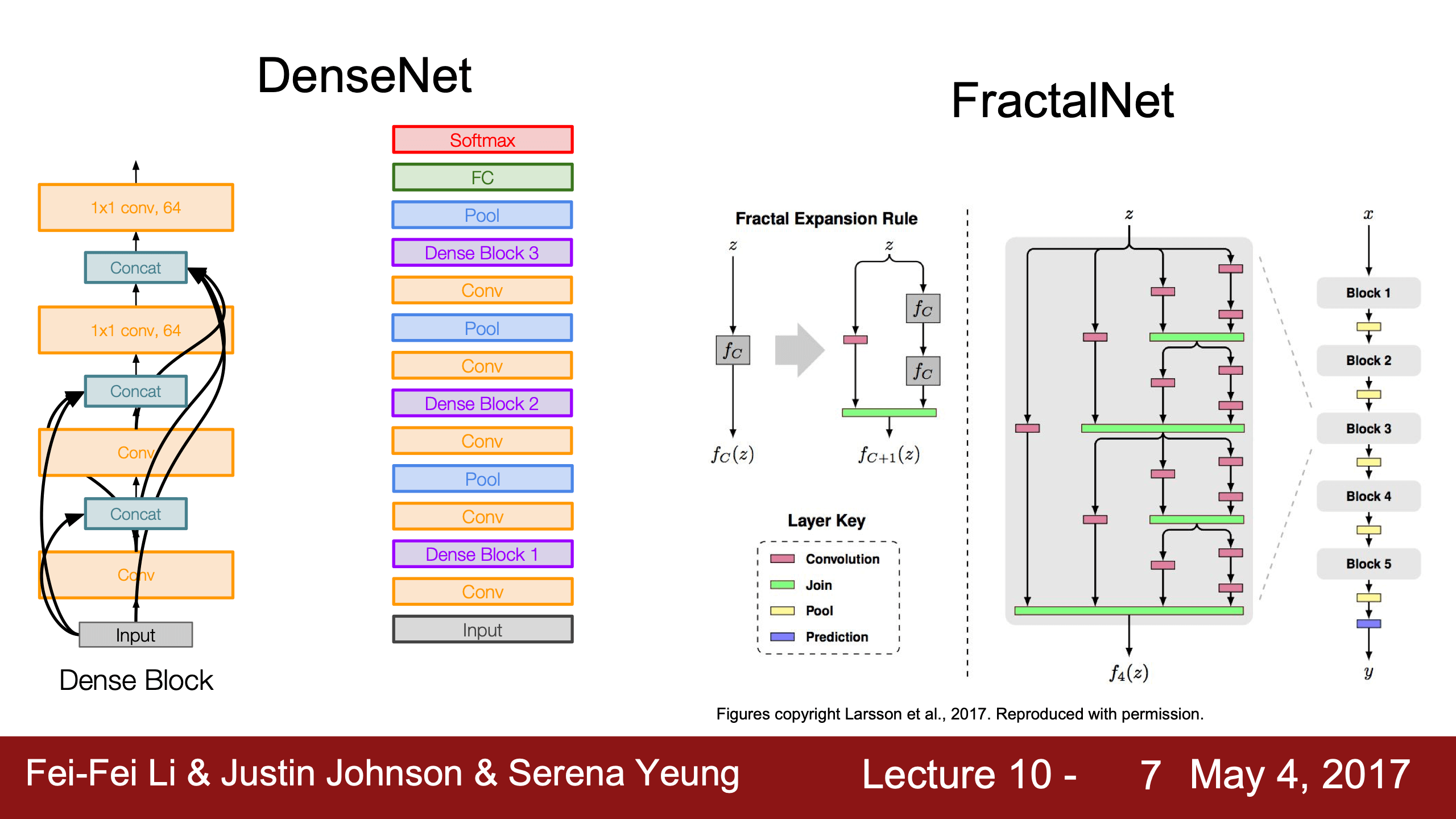
recurrent nn是Justin Johnson’s favourite topic.
循環nn vs. 递归nn
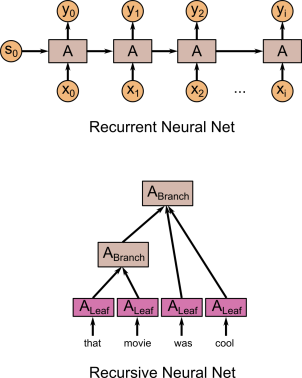
vanilla RNN
又叫做Simple RNN或Elman RNN。
每層用的W都是一樣的,更新 $\frac{\partial L}{\partial W}$ 的梯度則為每個time step的梯度之和:

computational graph:
 |
 |
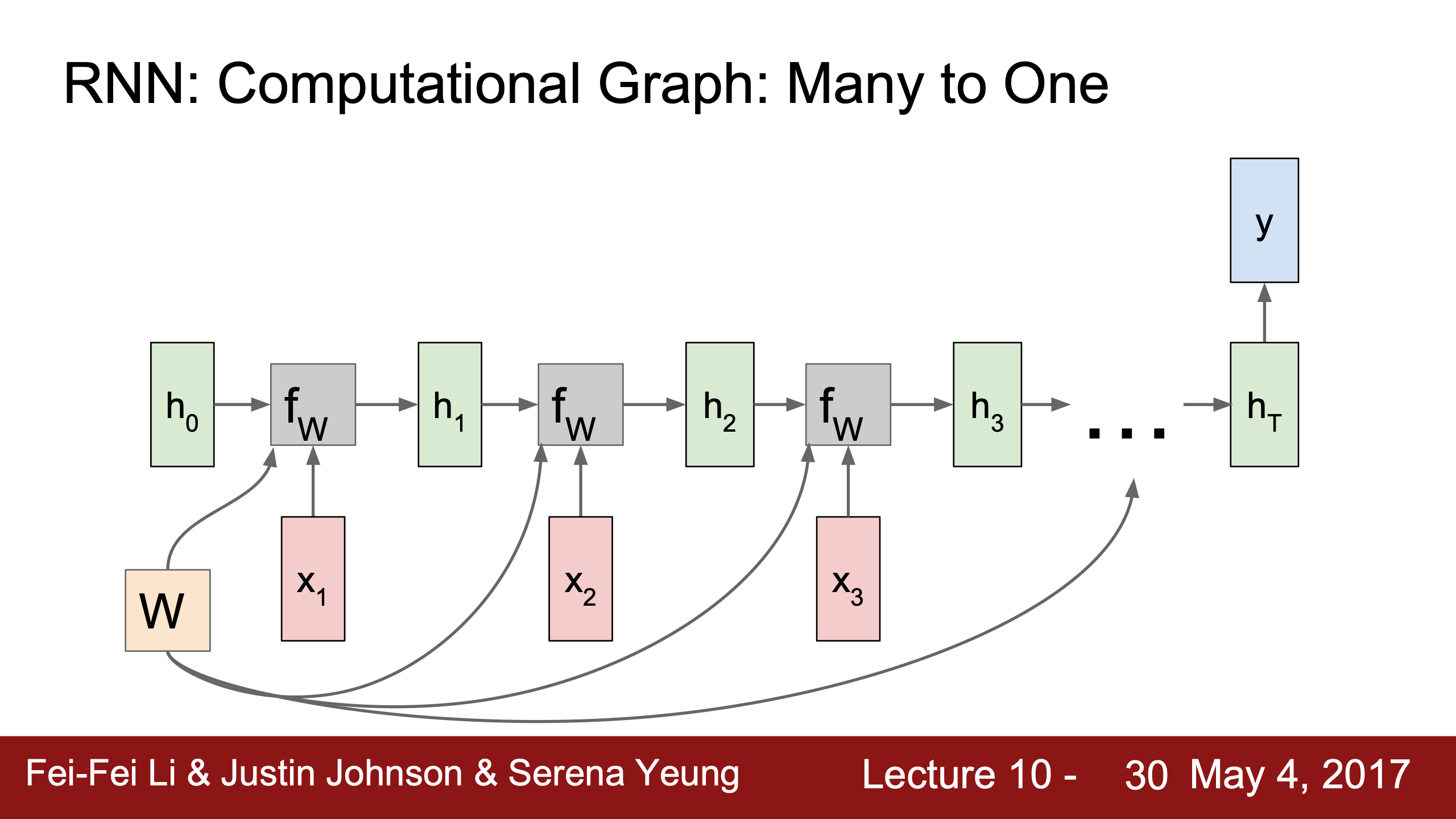 |
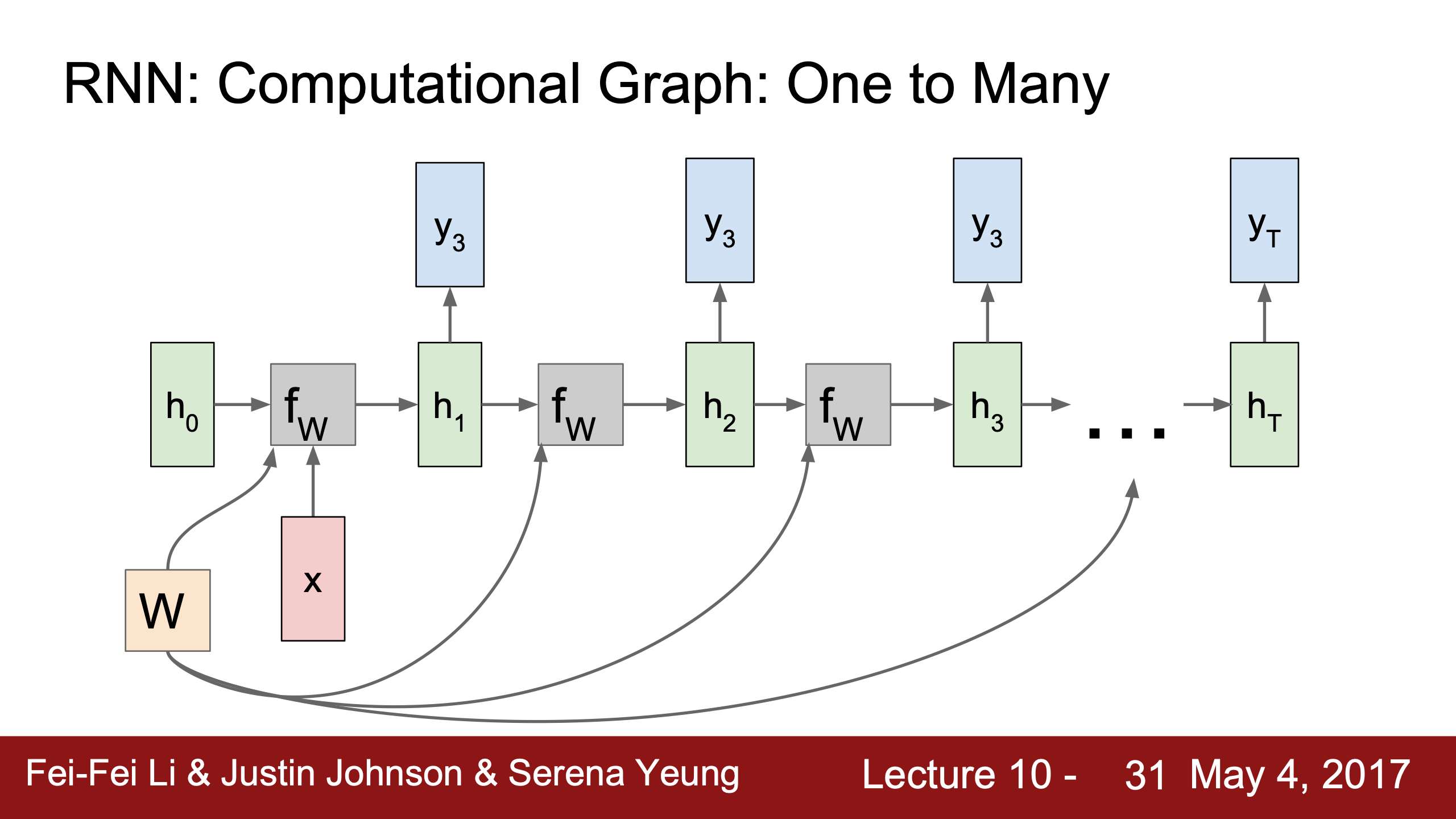 |
 |
最大概率argmax vs. 採樣sample, vanilla
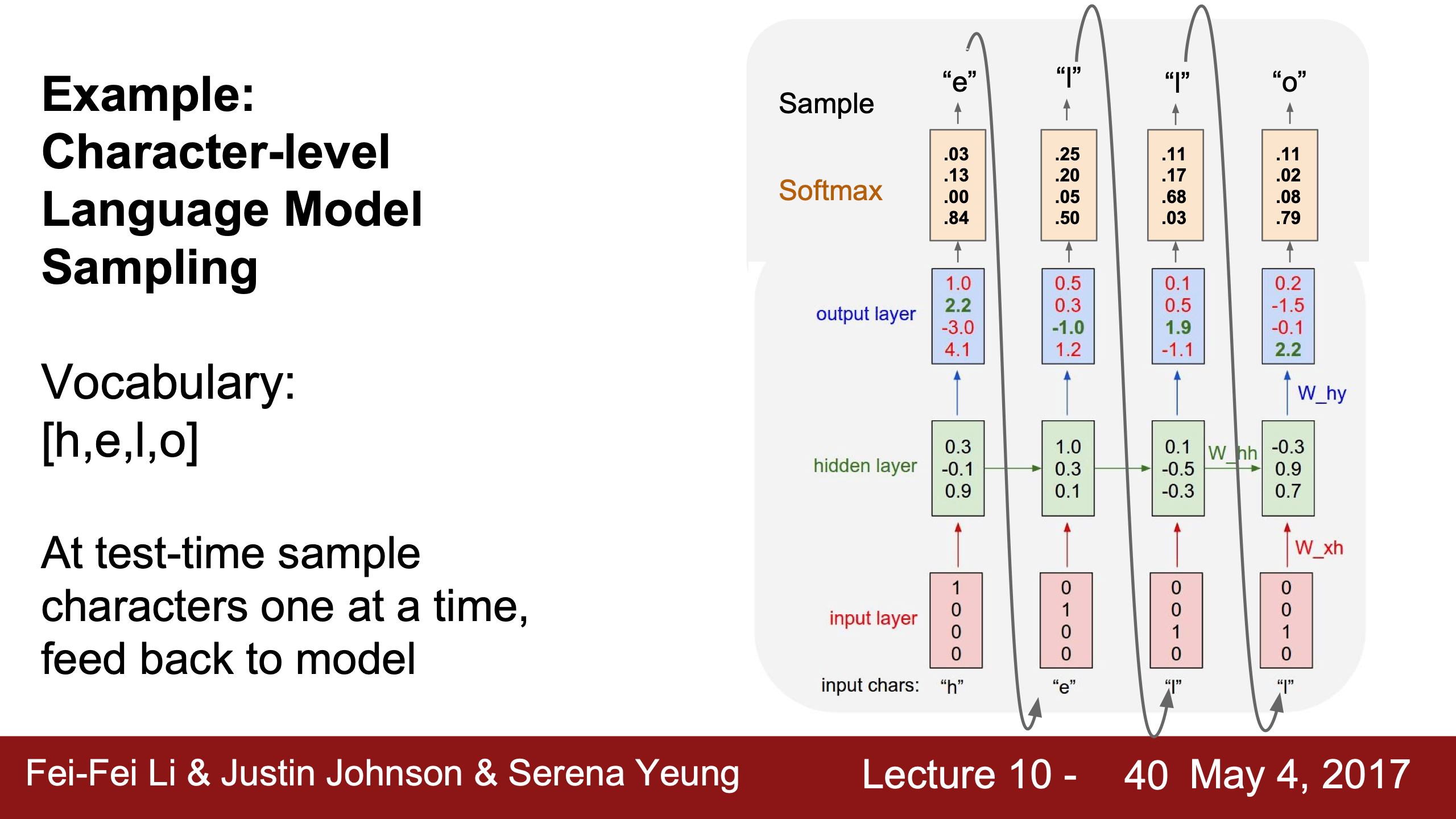
sampling是根據每個詞(輸出)的概率分佈進行隨機選擇,不是均勻分布的隨機採樣,哪個詞softmax後概率大被選中的概率就大。生成更多元、創造性或不確定的輸出,提高結果的真實感。
test time不用softmax用one-hot的原因:1.如果train/test給模型的東西不一致通常會輸出garbage;2.假如vocabulary是以萬計的詞表,用softmax這種dense vector會增加計算開銷,會傾向於用one-hot這種sparse vector。
這群同學問的問題都太好了。
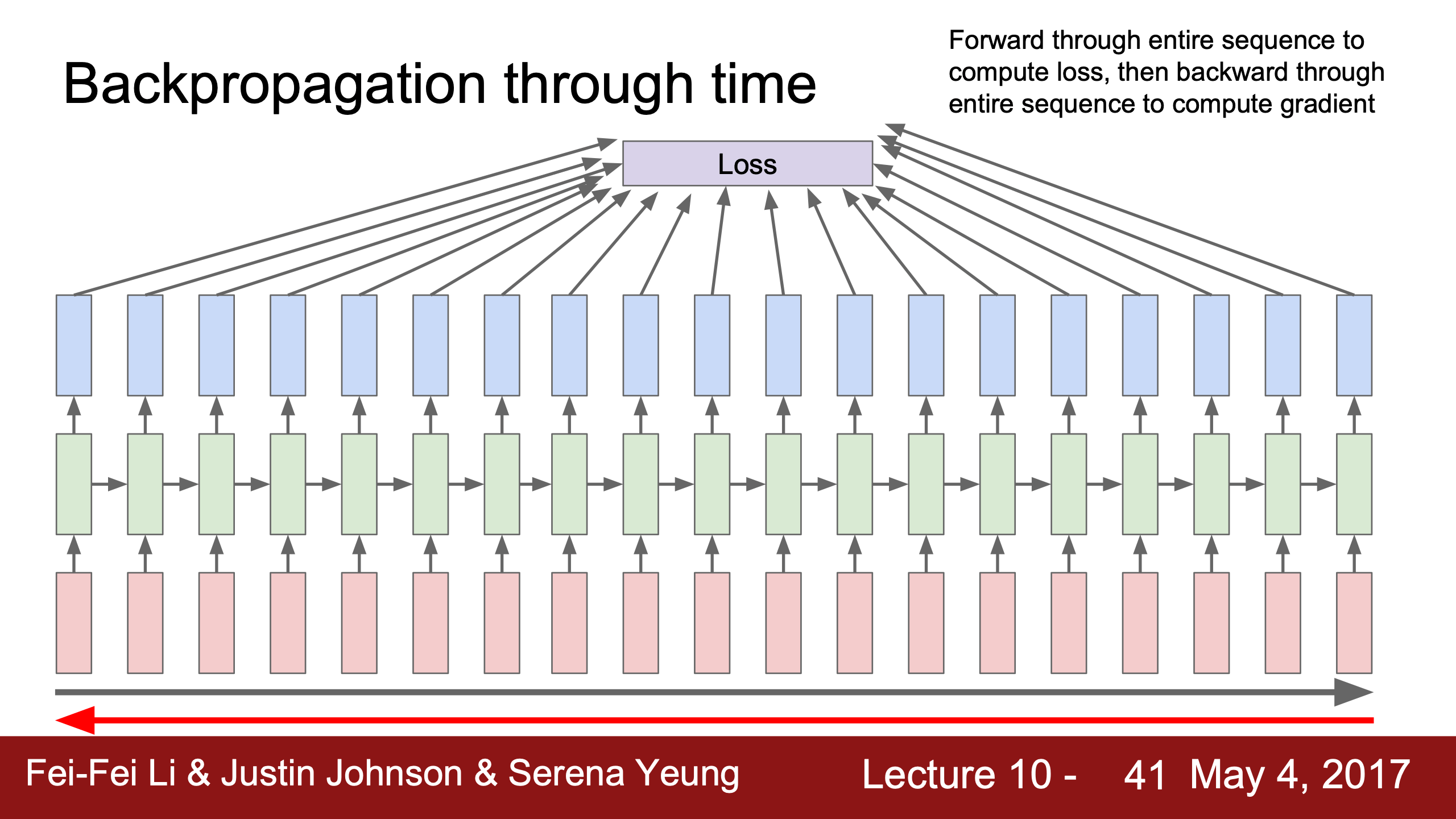
為降低開銷使用截斷反向傳播Truncated Backpropagation Through Time (TBPTT),其實類似於我們不做full batch的gradient descent而選擇用mini-batches的SGD,這裡只用幾百個time steps計算一次梯度。
vanilla rnn就講到這,剩下的JJ就讓自己看min-char-rnn的代碼了。
attention
| image captioning用CNN+RNN時,有很多組合的方式,比如把image information直接乘Weights加到第一個time step上。 | training階段在每個caption的最後都加一個<end>token(開頭加<start>),所以模型test階段會傾向於在最後採樣結束標誌。 |
|---|---|
 |
 |
可以用Microsoft Coco數據集從頭到尾訓練這樣一個CNN+RNN,也可以固定CNN最後的FC層,訓練RNN的時候捎帶更新FC。
| JJ還講到了第一篇用到hard attention(不可導,后面強化學習還要講)的文章Show, Attend and Tell: Neural Image Caption Generation with Visual Attention, ICML 2015 | 第一個在神經網絡訓練裡用soft attention的是Neural Machine Translation by Jointly Learning to Align and Translate, ICLR 2015 |
|---|---|
 |
 |
VQA也在用attention機制,image和word vectors的結合最常用的就是直接concatenation。
Multilayers RNN
多層也一般就三四五層,RNN沒有很深層的,LSTM也一樣。
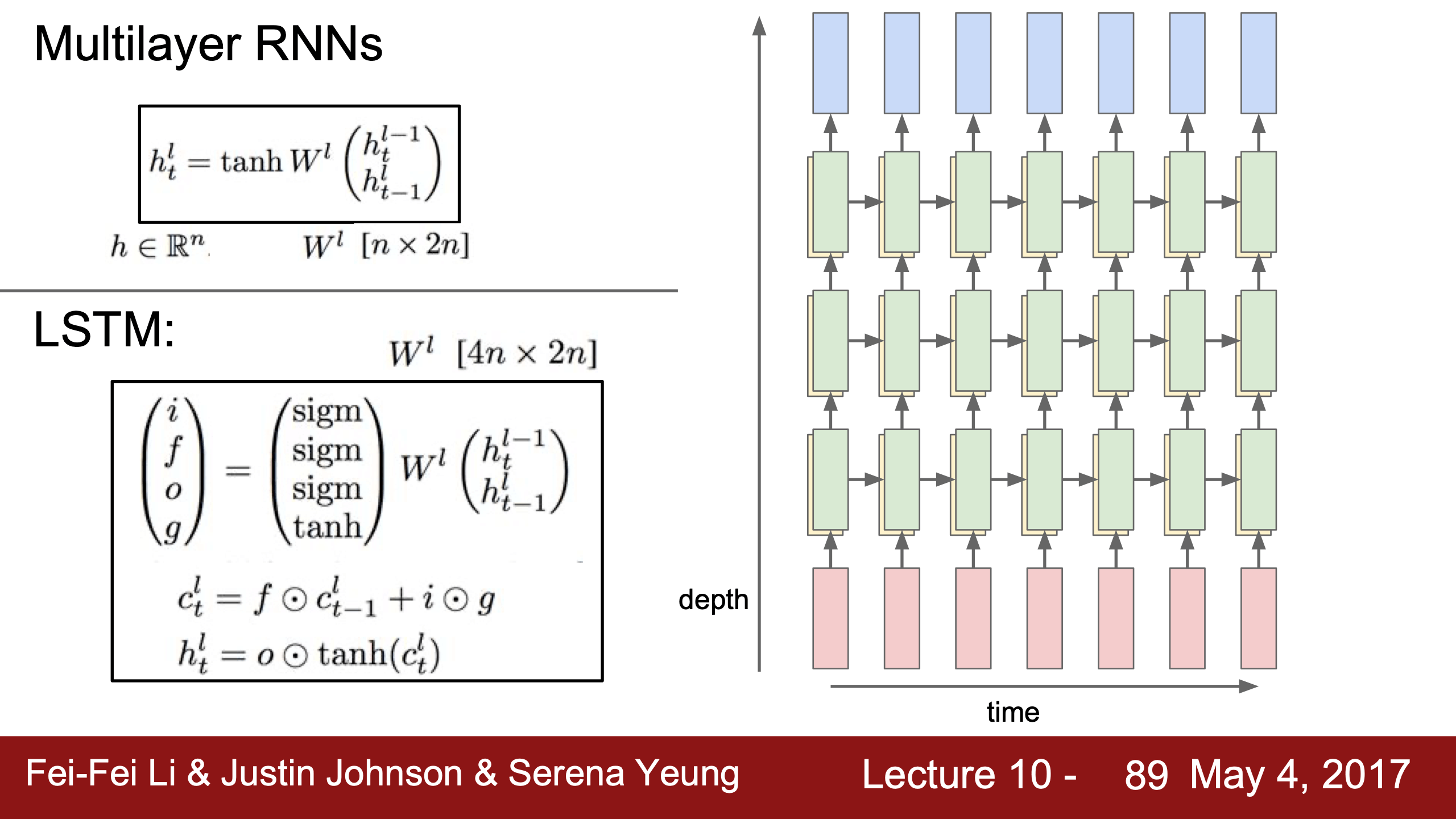
LSTM
因為向前面time step傳遞梯度時,$dh$ 會不停地乘 $dtanh$ (即 $1-tanh^2$ )和 $W^T$ ,這個值是不變的(截斷back prop也要很多time steps才update params),
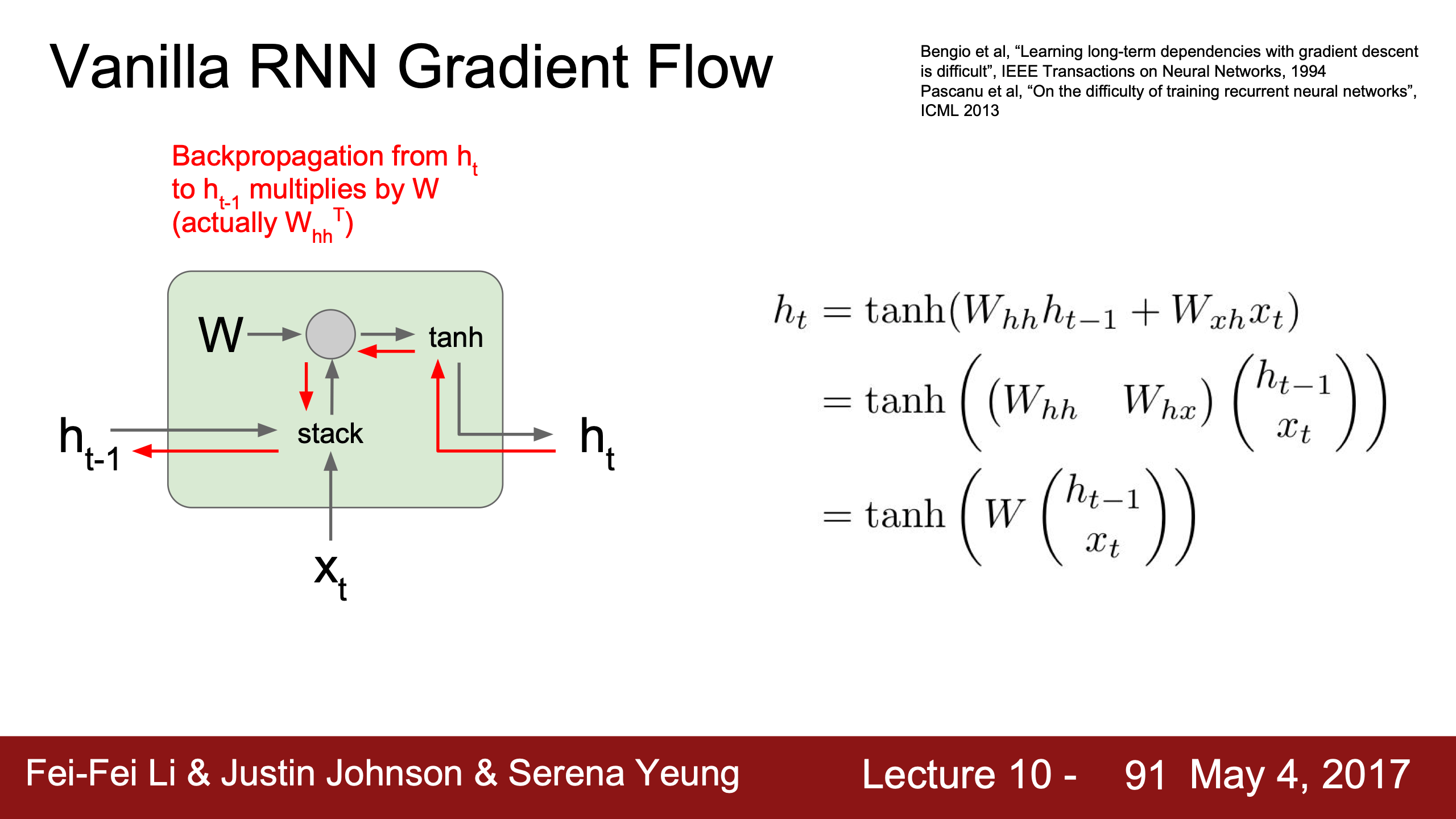
| 如果這個 $dtanh \cdot W^T$ 值大於1,傳遞到最開始的 $dh_0$ 就很可能梯度爆炸, | 小於1就很可能梯度消失。 |
|---|---|
 |
 |
解決方案是,太大就直接clamp截斷,為了應對太小的問題則需要其他RNN架構(LSTM同時能解決exploding和vanishing,已經是1997年的論文了,Long Short-Term Memory, Neural Computation, 1997, Sepp Hochreiter, Jürgen Schmidhuber (German))。
| 公式裡的 是指concatenation之後的vector,LSTM相比vanilla RNN除了hidden state $h_t$ 之外還需要maintain一個cell state $c_t$,$c_t$ 是個幾乎只在cell內部作用的內部量 | LSTM同樣是用這個stack的向量 ((h+x), 1) 乘一個大的W (4h, (h+x)),結果直接切分成4個(h, 1)維向量,然後分別通過3個sigmoid和1個tanh激活函數得到4個跟hidden state(h)維度相同的門gates(i f o g)。 |
|---|---|
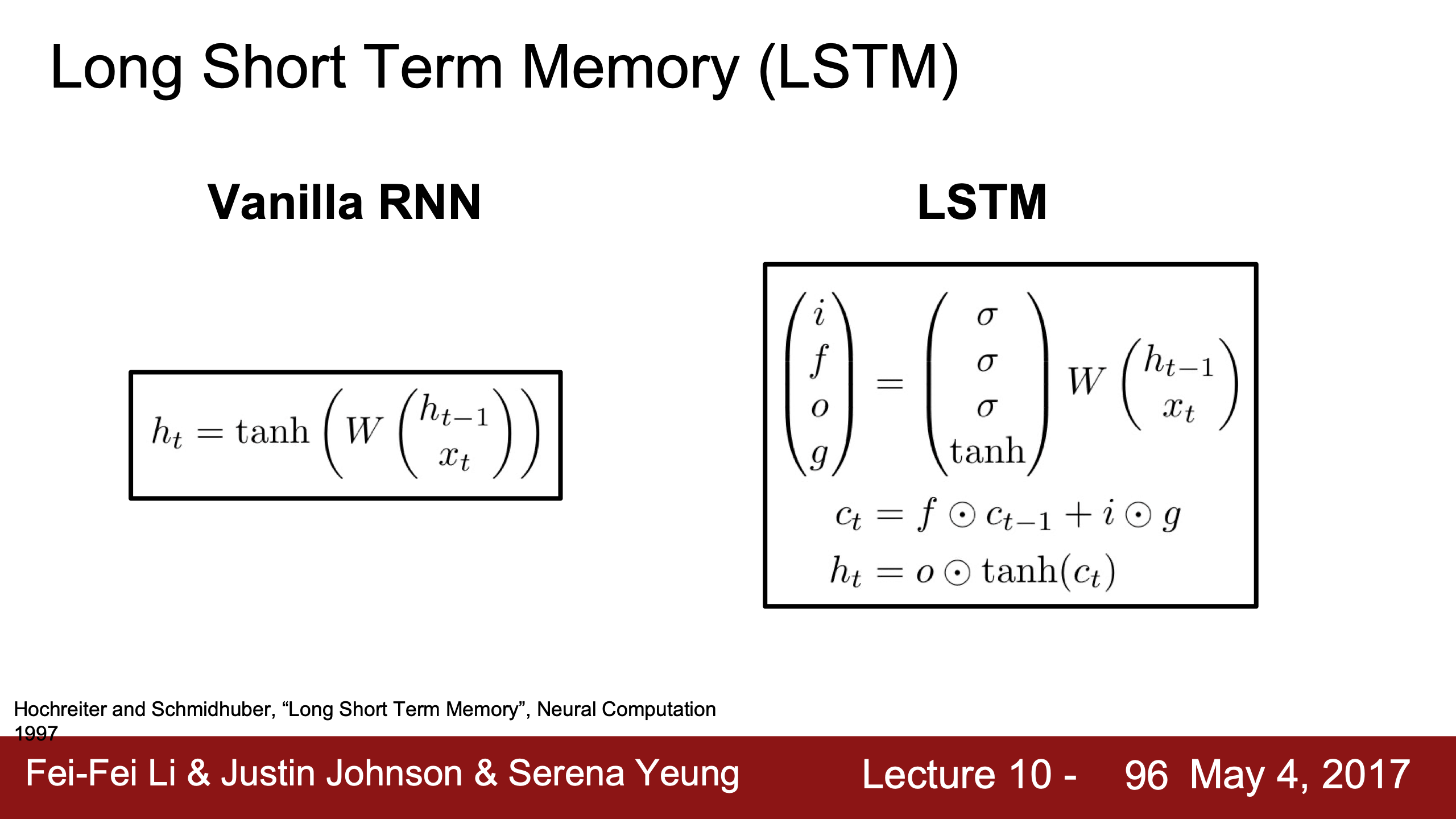 |
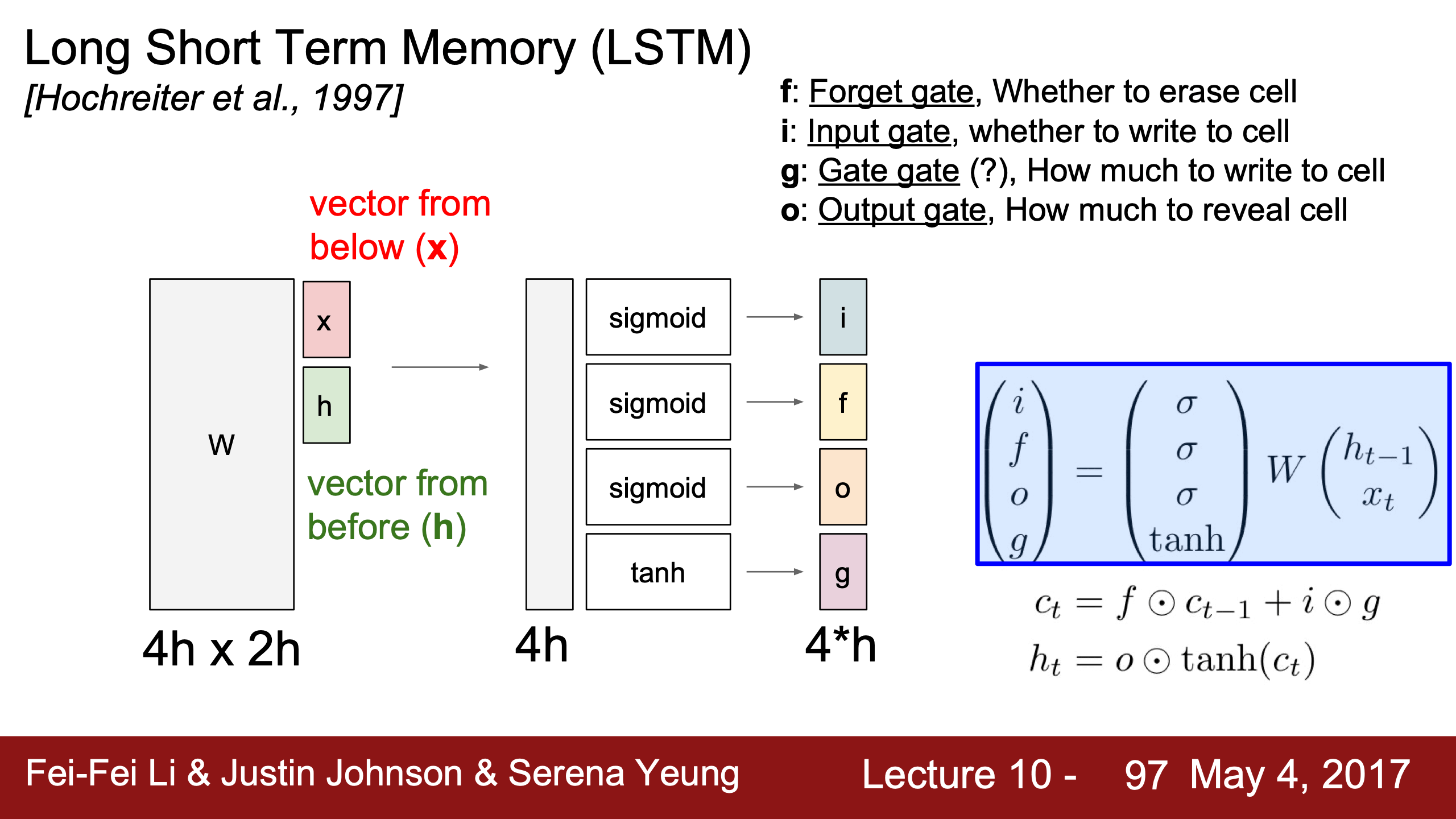 |
理解下右邊右下角公式:
- f是被sigmoid拉到0~1的值,跟cell state相乘可以理解成是否遺忘上一個時間的狀態,0為遺忘1為記住;
- i也是0~1,用於決定本個LSTM cell的信息是否被寫入cell state;
- g是-1~1的值,中文是“候選記憶單元”,是待寫入cell state的信息;
- 所以 $c_t$ 的更新規則為,除了決定是否記住/忘記上個cell state,每個time step還會加一個(-1, 1)之間的值;
- 所以其實 $c_t$ 類似於一個time step的計數器,每個time step ±1;
- 在計算完cell state之後,就用 $c_t$ 來計算真正暴露在cell外的外部量,hidden state;
- o是被sigmoid壓縮到0~1的值,$c_t$ 通過 tanh 被 squashed 壓縮到 (-1, 1)之間與 $o$ 相乘,所以 $o$ 用來決定是否把 $c_t$ 用於外部計算。
一個最直接的疑問可能是:這樣被壓縮到0到1之間的 $x_t$ 和 $h_t$ 不會造成信息損失嗎?——其實是不會的,不管那些“平滑變換”之類的說法,vanilla RNN本身和FC和CNN都是會用所謂的non-linearity把值 squash 到 0~1 或 -1~1 之間。
在本節最下面再討論一次激活函數non-linearity的問題。
| 上面的加法只會直接傳遞upstream,乘法會讓upstream逐元素乘forget gate f,1.這樣傳遞梯度只會有逐元素乘,优於vanilla RNN的 $dtanh \cdot W^T$的矩陣乘;2.這樣每個time step的梯度反向傳播不會不斷地反覆地乘一個W,而會是乘不同的0~1之間的f,這樣不容易梯度消失? | cell state這條通過additive和element wise multiplicative interactions傳遞梯度的highway跟resnet很像 |
|---|---|
 |
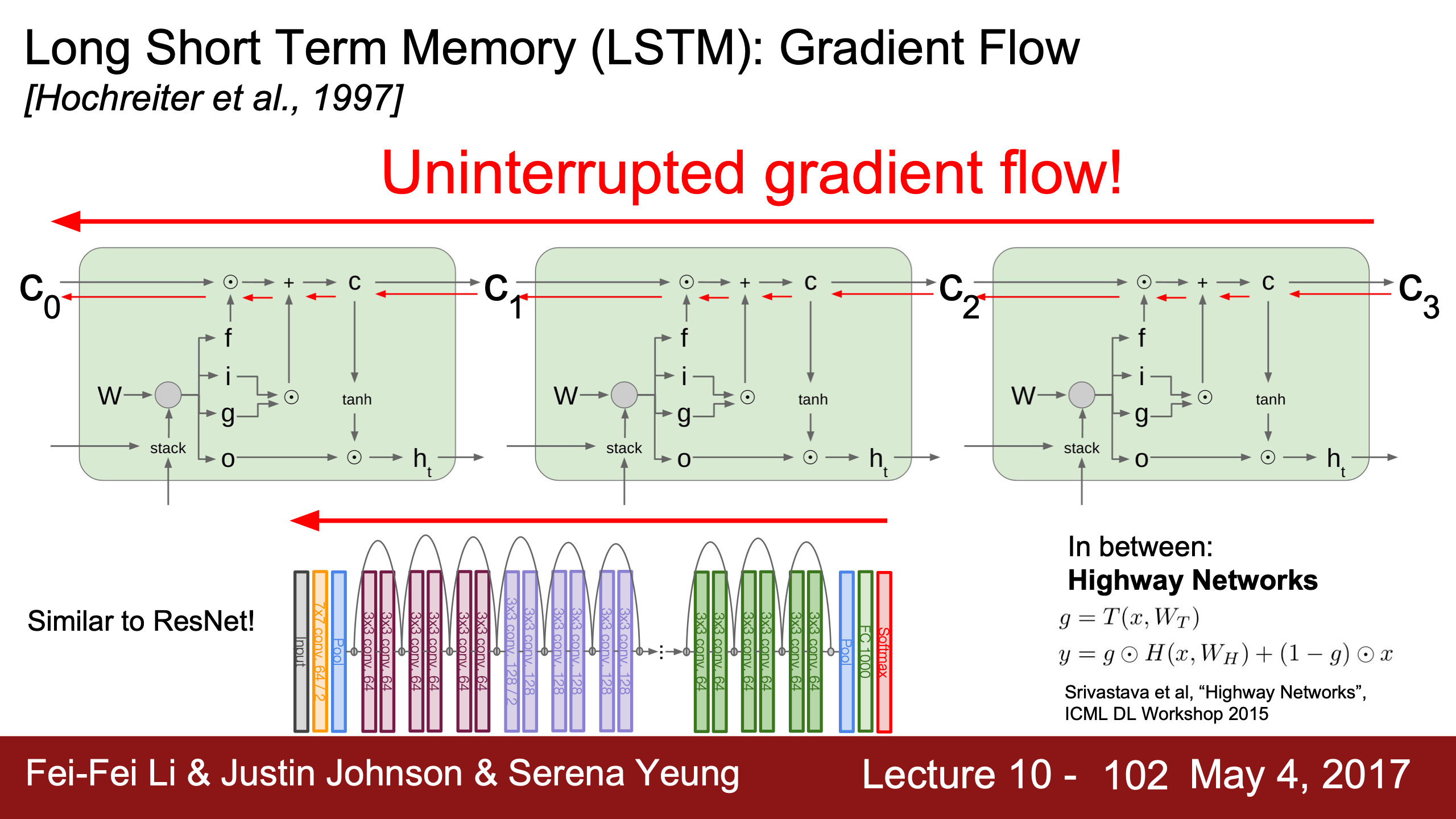 |
關於上面JJ說的的兩個好處我滿滿都是疑問:
- 為什麼只有逐元素乘?因為更新W是通過i f o g四個門更新的,這些正向都是逐元素乘操作,所以反向梯度也是逐元素乘;
- 但為什麼逐元素乘好過矩陣乘?不知道是說訓練效率還是模型效果;
- 為什麼反覆乘一個f不會導致梯度消失?f在0~1之間,就算一個位置一直是0.99經過100個time steps也會變成0.366!
- 說是乘W是固定一直乘一個,f是動態的,所以好;
- 說是傳遞cell state的梯度不經過tanh只經過加法操作(f i g都沒有tanh,只有o有,但是它們本身的sigmoid不會影響穩定性嗎?)梯度傳遞更穩定。
- 1:08:41原來JJ講到了!我太喜歡他們了——
- 說是確實會有這種問題,所以在實踐中大家可能會把forget gate的biases都初始化為正數,所以在訓練剛開始時forget gate會一直接近1保證乾淨的梯度流,
- 確實仍然會存在vanishing的問題,但是會比vanilla RNN好非常多,就是因為1. forget gate是變化的,而且2. 是元素乘不是矩陣乘。
總之我們關心的只有W和dW,原本的RNN的 $\frac{\partial L}{\partial W}$ 只會通過h傳導而存在不停乘 $W^T$ 的問題,現在LSTM的 $\frac{\partial L}{\partial W}$ 同時通過 c 和 h 傳導,而 c 的梯度相比 h 有以上那些好處,所以回傳的梯度會更乾淨更穩定。
Takeaway:
後來二十多年的研究裡並沒有效果全面超過LSTM或GRU的,可能某一個任務強但是其他任務弱。
可能直接用LSTM或GRU不會有什麼神奇的效果,但是通過添加 加法additive connections 和 乘法門multiplicative gates 來讓梯度流更合理地反向傳播的思路往往很有用。
激活函數non-linearity
sigmoid、tanh、relu的目的是对数据进行平滑变换,不會丟棄信息,通过将输入映射到一个新的范围,使其在更合理的范围内流动,而不会出现过大的数值波动(避免梯度爆炸)或数值消失(避免梯度消失)。
它們基本都保留了輸入信號的大小和方向,而且能允许网络捕捉复杂的非线性关系。
在上面Lecture 4那也想過相關問題,“這裡其實我一直有個疑問,如果X裡有x1 x1x2 x1x2x3這種高階特徵,那豈不是不再線性了?這個問題其實有點蠢,因為線性關係是指x1和f(x1)、x1x2和f(x1x2)、x1x2x3和f(x1x2x3)之間是線性/直線,而不是x1x2/x1x2x3跟f(x1)”。
Lecture 10 Summary
- RNNs allow a lot of flexibility in architecture design
- Vanilla RNNs are simple but don’t work very well
- Common to use LSTM or GRU: their additive interactions improve gradient flow
- Backward flow of gradients in RNN can explode or vanish. Exploding is controlled with gradient clipping. Vanishing is controlled with additive interactions (LSTM)
- Better/simpler architectures are a hot topic of current research
- Better understanding (both theoretical and empirical) is needed.
RNN本身效果太差,用就用LSTM,雖然equations看起來crazy,但是make sense,因為優化了backprop gradient flow。
Lecture 11
HyperQuest它們開發完了,對他們同學有extra credit的調參遊戲,有空(when?)跟上面之前幾個demo一起玩一玩。
之前的主題都是image classification,這節課講detection/segmentation/localization和其他tasks。
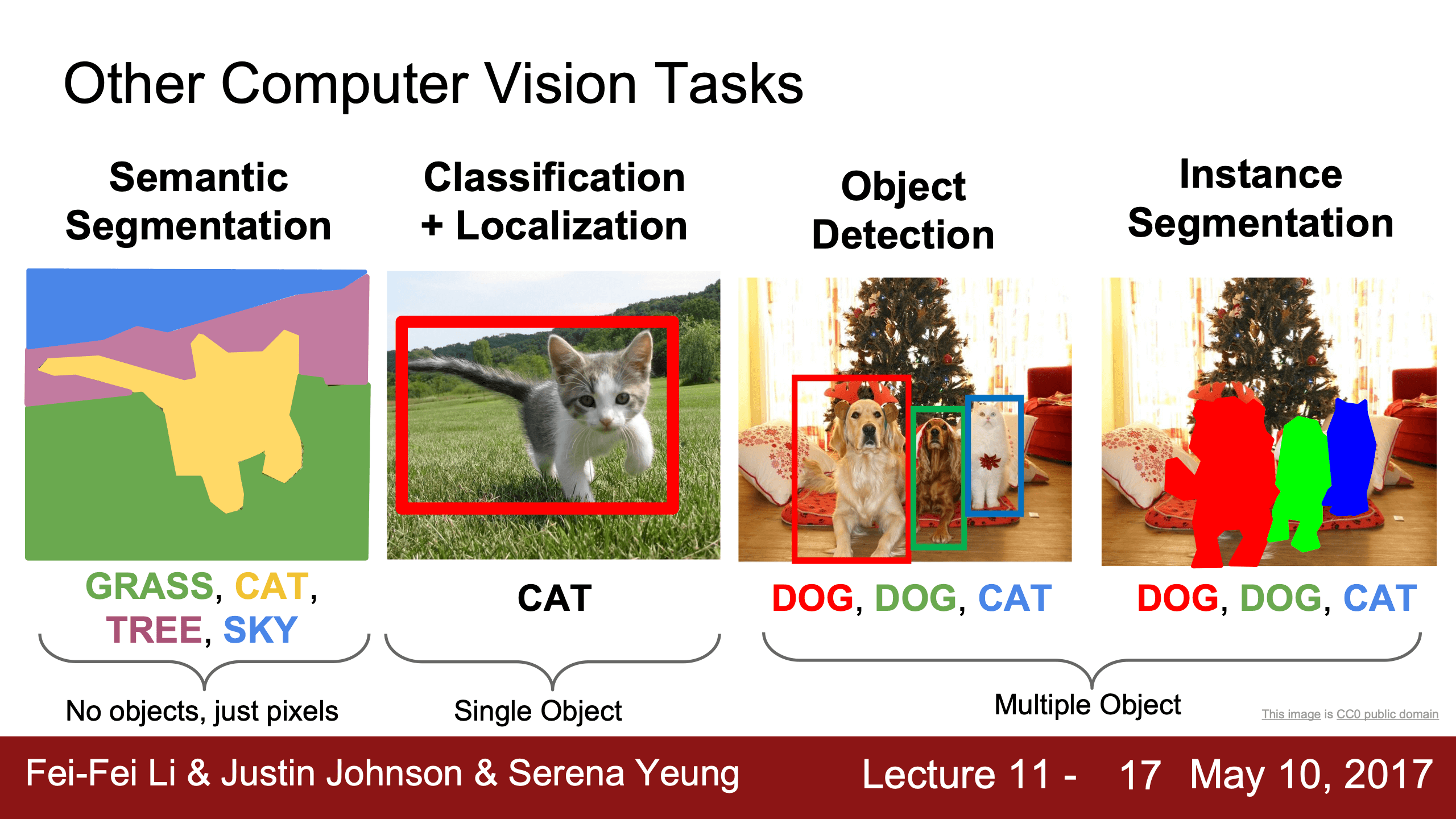
Semantic Segmentation

語義分割任務目標是給每一個像素分一個label,這裡跟圖像分類一樣,數據集裡我們關心的類別是10個100個1000個提前確定的類。
右邊不區分兩頭牛都打上cow是語義分割的一個短板,instance segmentation實例分割會解決這個問題。
所以這類任務的數據很昂貴,需要用軟件手動畫邊界。
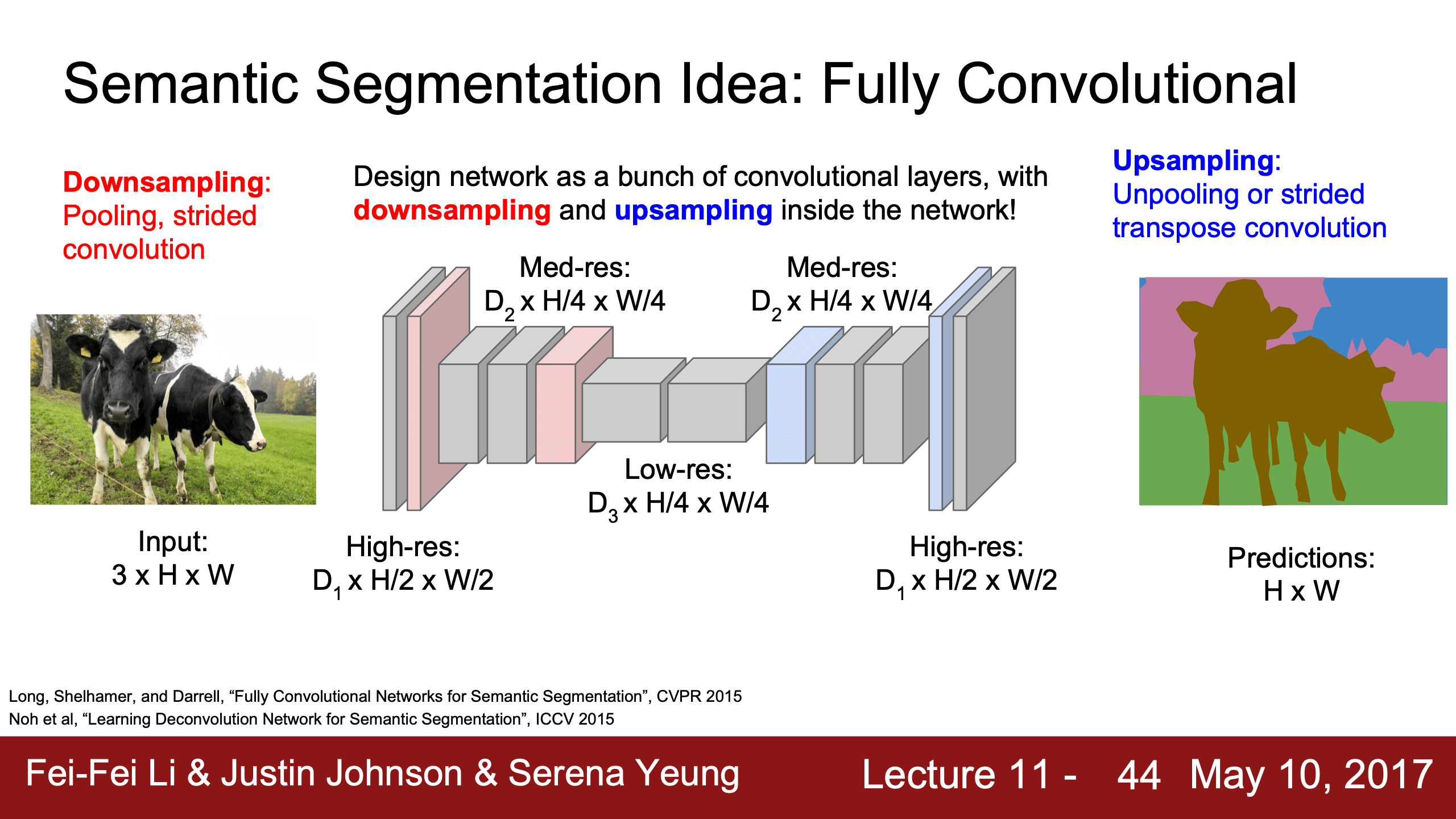
| 對應降維的pooling層,升維時是unpooling/upsampling,即復原MASK其他的位置都補0。 | 對應降維的conv層,升維時還是用filter走stride,只不過把conv的內積變成逐元素乘。 |
|---|---|
 |
 |
| 用矩陣乘表示convolution操作的話,現在的升維convolution就是輸入transpose一下,這裡是stride=1的演示 | stride = 2 |
|---|---|
 |
 |
transpose convolution真是個好主意,叫做”transpose”也真的很聰明,但其實也就是玩維度遊戲,剩下的一切交給optimizer罷了。不要叫deconvolution,因為反卷積不是這個操作。我在上面cnn convolution部分討論原初的signal processing convolution的地方補充了反卷積的概念,以及改掉了一開始chatgpt的錯誤例子。
用的都是很熟悉的模塊,但是稍加修改立刻就能應用到其他任務上,這super cool也super 爽。我的論文可以學這裡把模型遷移到其他任務的思路,兵來將擋水來土掩,包括diffusion和transformer之外用上面的LSTM機制會看起來很屌。
Classification + Localization
這個任務跟目標檢測object detection的區別是,Classification + Localization 分类 + 定位任務事先假設只有 1 個目標或者exact多個目標只生成exact 1 個bounding box邊界框。
| 如果這個multitask loss不是直接加起來,而是用一個weight做weighted sum,那麼就需要一個loss之外的metric衡量performance,因為一般我們調超參都是以loss為指標,換幾個hyper parameters看loss怎麼變化,但這個weighting parameter是會直接影響loss值的 | 這個任務可以應用到其他地方,比如Human Pose Estimation人体姿态估计。 |
|---|---|
 |
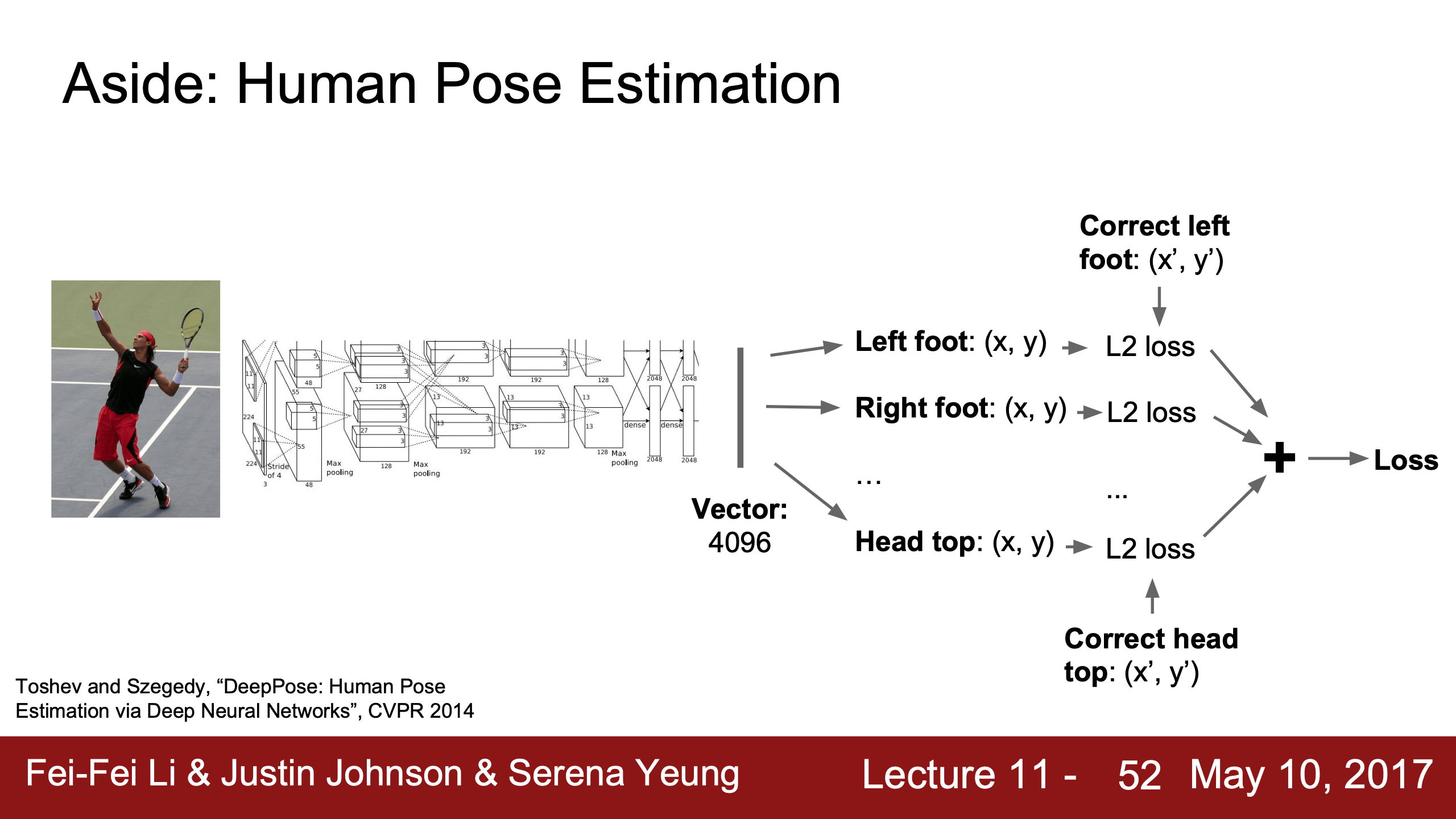 |
- 把兩條路合成一個可行嗎?未必,這裡只是basic setup。
- 那如果不把兩個loss合成一個multitask loss而是分辨訓練兩個FC呢?JJ說在Transfer Learning時Fine Tune Jointly(聯合訓練)永遠效果都好過分開tune,因為features的mismatch,但是也有一個trick是分開訓練完都converge收斂了,再合在一起jointly訓練一下,這樣也是可以的。
這裡同學的一個問題很好:為什麼這裡JJ說Human Pose Estimation用“regression loss”,指的是什麼?
JJ說他指的就是cross-entropy(softmax)或者SVM loss之外的loss,比如L2和L1 loss,如果你希望輸出是離散的(如classification)就用softmax loss(classification loss),如果希望輸出是連續的(比如這裡)那就用L2(regression loss)。
單獨討論一下回歸問題和分類問題吧。
回歸vs.分類 (Classification vs. Regression)
簡單來說,
- 回归是預測連續值,使用MSE (Mean Squared Error, 均方误差) 损失函数。
分类是預測離散值,把數據分配到離散類別,使用交叉熵损失函数。
- MSE确实可以用于分类任务,但它并没有交叉熵损失那么直观且有效,尤其在处理概率和梯度更新方面。
- 交叉熵更适合分类任务,它是专门为概率分布设计的,能够更好地处理类别之间的关系,并且有更稳定和有意义的梯度。
假设我们有一个二分类问题,类别0和类别1。
- 模型的输出为0.7,表示模型认为它属于类别1的概率为0.7。
- 真实标签是类别0(即标签为0)。
$\text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2$
MSE = (0 - 0.7)² = 0.49
$\text{Cross-Entropy Loss} = -\left( y \log(\hat{y}) + (1 - y) \log(1 - \hat{y}) \right) = -(0 \cdot \log(0.7) + (1 - 0) \cdot \log(1 - 0.7)) = - \log(0.3) \approx 1.204 $
可以發現,
- 交叉熵的loss更大,即對錯誤的懲罰更大,錯得越離譜用log就大得越多;
- 還是因為這個對數,對數曲線是越接近0時越陡,根據上面的公式模型預測越錯誤log的自變量就越接近0,梯度就越大,模型更新得就越快。
反過來看回歸的例子:
- 假如我們在預測房價,一個數據的真實房價是3.5,預測值是3。
$\text{MSE} = (3.5 - 3.0)^2 = (0.5)^2 = 0.25$
但是用交叉熵根本沒法處理,因為這裡沒有類別,假如想強行使用交叉熵得發揮想像力,比如把連續值離散化為類別,房價離散化為區間:
- 类别1:( [3.0, 3.5) )
- 类别2:( [3.5, 4.0) )
那 $y = 類別2$,$\hat{y} = 類別1$,而且這裡錯誤類別的預測值也得假設,
這裡預測值是3.0,就得假設 $\hat{y}_{類別1} = 0.99$,假設 $\hat{y}_{類別2} = 0.01$ 這樣。
雖然能算,但是幾乎沒法算。
結論:用同一個模型可能既可以處理regression又可以處理classification,但是需要構造不同數據 且 需要改loss function。
Object Detection
這個領域的歷史和研究足夠講一個學期,是非常meaty的問題。
任務描述:
- 同樣是some fixed set of categories;
- given image:每次上述categories裡的一個出現在image裡的時候, 我們希望得到一個bounding box和它的類別label。
跟Classification + Localization不同的是每個image都可能有不同數量的outputs。上課時的數據集多年來相對常用的是PASCAL VOC,但因為15年以後mAP一直80%以上,很多人因為這個數據集的任務太簡單而轉用其他數據集了。
| 把目標檢測想成是regression回歸任務有些麻煩(輸出連續值坐標), | classification比較好(離散值),用熟悉的滑動窗口sliding window,但問題是需要滑動的位置太多了! |
|---|---|
 |
 |
這裡的類別在categories之外會加入一個additional category: background。
| 針對sliding window滑動位置太多的問題,自然想到事先選定一些窗口,即Region Proposals。左下角是一些region proposal算法(Selective Search/EdgeBoxes),都是在CPU上完成的。 | 基於這些算法,優化版的sliding window出現:R-CNN |
|---|---|
 |
 |
R-代表region,region-based cnn。
- 也是個multi-task loss,svm判斷label,然後會有個Bbox reg的correction項,把region proposals出來的bounding box再修正一點,svm預測的是離散標籤所以是classification,預測的Bbox reg是連續值所以是regression。
- 這裡提取的RoI的aspect ratio寬高比?大小如何影響結果?JJ不確定相關實驗結果。
- RoI可以是非rectangles嗎?說是在其他任務比如instance segmentation裡region proposals可能不是矩形。
- R-CNN裡region proposals不是learned的,是固定的傳統的算法,但後面會有基於這個改動的算法——Fast和Faster用另一個CNN(RPN)學到。
- RoI裡沒有objects的也是都會輸出background。
這類數據的獲得構建也有論文,比如如果只有一些圖片有bounding box數據?如果數據有噪聲(like誤定位誤分類?),這些問題我的論文也可能遇到。
這部分寫作業不知道2017年和2024年哪邊有,最好還是實現一下,看過很多次了包括前些年看李沐老闆上課時讓實現這塊兒讓我負責講這塊兒slide到現在還是不懂。
實在是太慢了,訓練在cpu上,要花 80 多小時,要很多disk,而預測一個圖片要花將近 1 分鐘。
Fast/Faster R-CNN
| Fast R-CNN裡region proposals的做法是,不直接對圖片取region,而是對CNN處理後的feature map取region。 | 訓練仍然是multi-task loss |
|---|---|
 |
 |
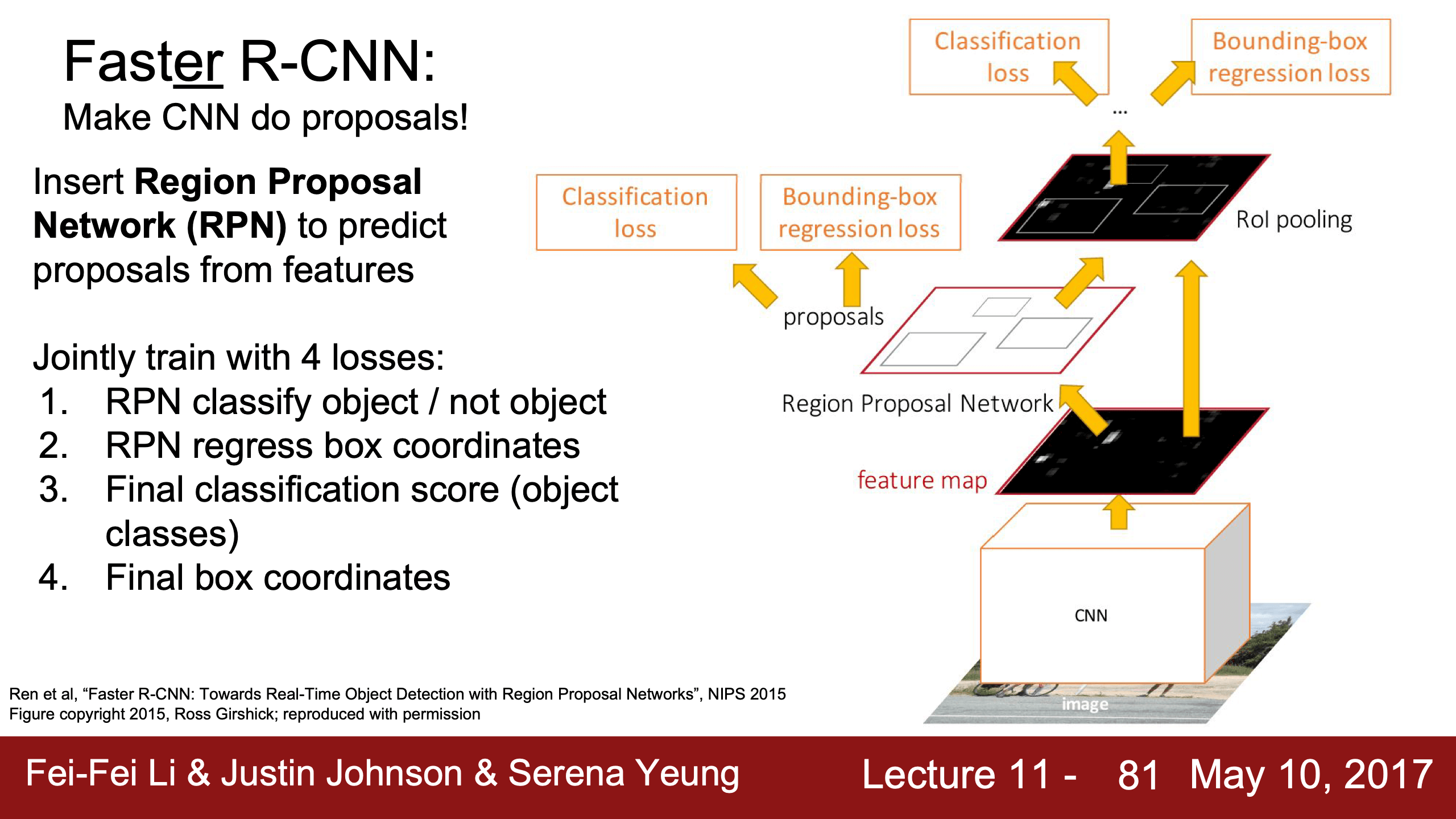
- 讓bottleneck的region proposals直接由RPN網絡提供。不再被這一步算法限制速度(Fast R-CNN雖然是在feature map上提取但還是慢)
- Fast R-CNN和Faster 都有一步 RoI Pooling 層,vanilla R-CNN是手工裁剪 region 為相同大小 RoI 給 CNN,不是 Pooling。
JJ說是文章裡有提到,如果region proposals的network跟classification的network分開呢?實驗結果是區別不大所以選擇計算開銷低的只用 1 個sharing network。
還有個同學問到了關鍵問題——怎麼設計的region proposals這部分的loss?JJ說基本思路是看region跟ground truth bounding box的重合率,重合高過threshold就positive反之negative,但是這些都是黑魔法超參數很hairy。loss是個二分類的loss,會在模型生成的一堆regions裡面分類。。
或者不分成兩個階段(region proposal + classification),而是一個模型一步到位。
YOLO/SSD
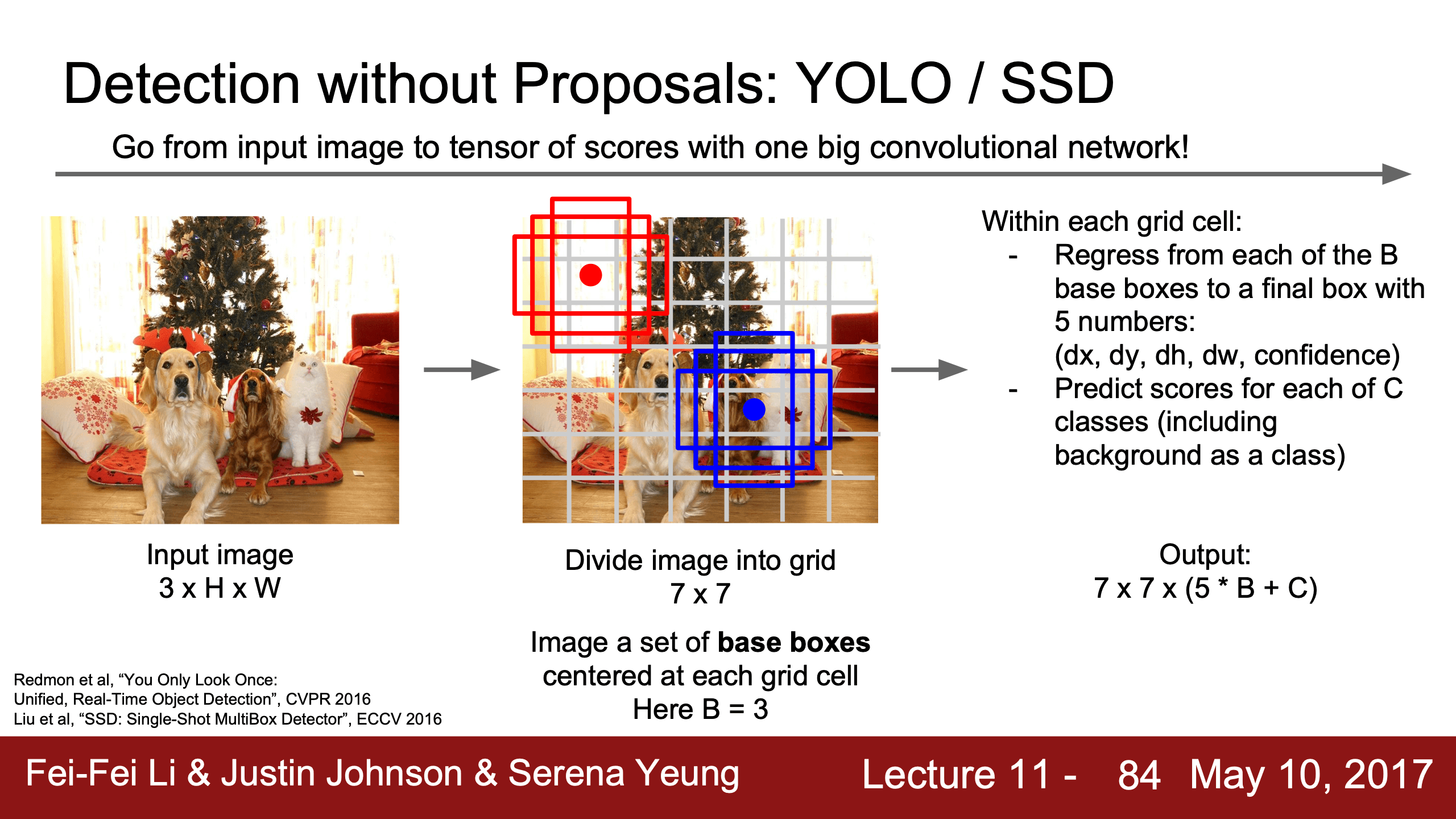
沒有region proposals,首先把input分割成 7 x 7 grid cells,每個 grid cell 以中心為 anchor 創造 B (>=3) 個 Base Boxes,對每個 base boxes直接預測 (dx, dy, dh, dw, confidence),和類別分數。
Base Box(基础框)Anchor Boxes(锚框)
grid cell實踐裡一般會超過3個,confidence是bounding box裡存在object的confidence。
Instance Segmentation
任務描述:類似object detection + semantic segmentation,不只想要bounding box,需要objects的segmentation mask。

用MSCOCO (200,000 images, 80 categories, 5 or 6 instances per img)。
Lecture 12
整個visualizing和interpretation都是不希望neural nets對人類只是數字很好看的黑箱,不能解釋如何做出的classification decision就似乎無法被信任,不像隨便什麼linear regression、random forest、decision tree都能直觀理解weights而被解釋。
Weights Visualization
 |
 |
這些Visualized Filters是彩色因為都是first layer的,數據是3 channel的第一層conv filter當然是3 channel的。N, C, H, W或者F, C, H, W四個維度,cnn那節或者在上面套路改變array形狀時實現過的。
Last Layer Visualization

尋找最後的特徵向量的nearest neighbours,發現確實學到了一些語義特徵,比如在圖像最左側的大象和最右側的大象是nearest neighbour(對原images用L2或者L1算KNN是不太會得到這麼好的結果的),在普通的supervised learning裡比如cross entropy loss並沒有要求這些feature相近,這只是個happy的發現,但是contrastive loss和triplet loss是顯式地要求同類features相近。看到這兒終於想起來三年前的種種往事,下回了久違的keynote,看了第一次組會拖了一個月的slides,老闆

dimensionality reduction也可以visualize what’s going on in the last layer,用PCA把高維數據降為2維就能可視化了。t-SNE (t-distributed stochastic neighbour embeddings) 是個更好的非線性算法,這裡直接聚類了m-nest dataset的數據,也可以聚類最後一維的features,這裡的做法是用t-SNE處理這個4096-d的feature得到一個x,y坐標,然後用feature的原圖代入進去。
Activations Visualization
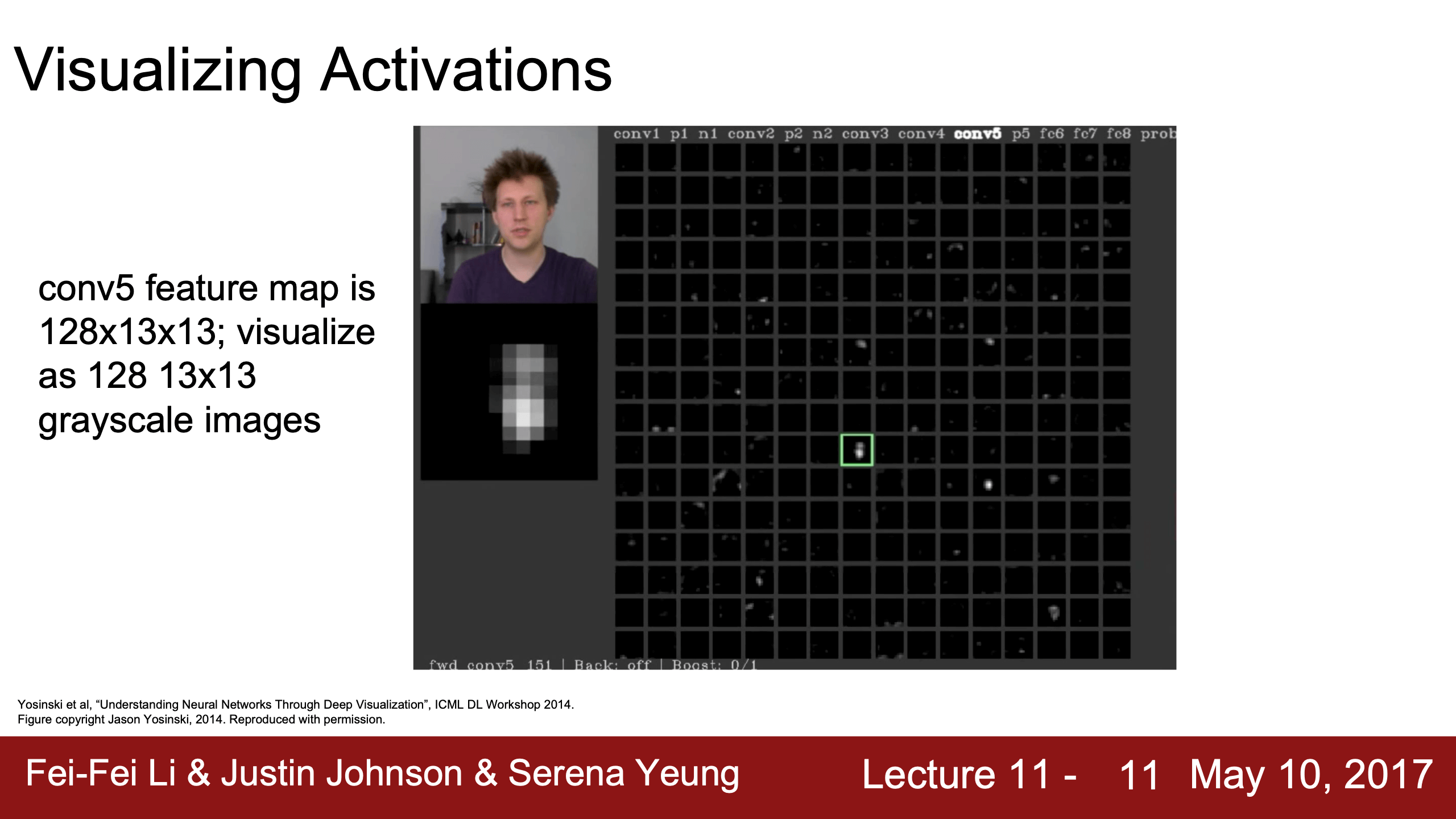
visualize weights可能不是很interpretable,但是activation map有可能比較interpretable。黑的是沒有active的激活函數,(不是dead relu,dead relu是說整個訓練都接收負值的)這裡所謂的activation map是每個conv filter輸出的大的3維數據的activation volume的一個切面(1, H, W)(我剛意識到輸出不是四維的嗎?喔N是數據量,展示的只是1個數據的模型)

activating patches也是個思路,這裡每一行都是conv5的激活層的某一個neuron?這裡的neuron就是比如relu的輸出值scalar。還是某一個channel的neurons?因為一個channel的neuron都是由同一個weight的filter產生的,比如第一行的這個neuron可能在找淺色包裹的深色圓形物體。因為深層的一個像素receptive field比較大所以能相較edge檢測更大的物體。

occlusion這個實驗思路是,用一個occluded patch (用image mean遮擋的區域)滑過圖片每個區域,在每個地方用模型生成一個目標分類的probability,比如elephant,把滑過每個地方的分類到elephant的概率合起來畫成一張heatmap熱力圖,基本思路是如果遮擋住某個部分讓分類概率大幅變化,那麼這個部分就對分類決定很重要。really import to classification decision

saliency map在2017年的assignment3裡,思路是直接對輸入的每個pixel計算gradient,其實一般我們不會算第一個dx,居然發現效果很不錯,同學提問JJ說確實可以用來做semantic segmentation problem。
guided back propagation能更好體現哪些真的在影響neuron的scores,JJ說想看細節得去讀paper。(跳過這個idea)

到目前為止都是給網絡固定的圖片,求解哪一部分哪個neuron最感興趣,但是也可以求解in general,使用gradient ascent,fix the weights, synthesize the image to try to maximize the scores of intermediate neurons or classees。
這裡也要加regularization,可能只是生成的圖片的L2 norm,不加reg的話可能看起來像random noise?然後初始化一個image,喂給訓練好的模型,計算感興趣的class/neuron wrt image的梯度,然後往梯度方向(argmax)而不是梯度反方向(argmin)改變圖像,生成的圖片很有意思。顏色很亂是因為可視化很tricky,因為我們要把gradient ascent的結果限制在0~255之間。
Fooling Image/Adversial就可以基於這個做法,把初始化圖片換成一個隨機圖片比如elephant,然後選擇一個隨機類別比如koala bear,然後用這個gradient ascent讓image maximize the class,最後可以生成人眼看起來一樣(居然沒變,difference也基本看上去只是noise)但是會分類為koala bear的圖片,即欺騙圖像。最後一節課lecture 16 Ian Goodfellow (這哥們兒姓“好人”?)會細講,這個也在作業裡。
DeepDream這個公式怎麼來的,56分JJ簡單算了一下沒聽懂。

Feature Inversion用到了Total Variation regularizer(encourages spatial smoothness),用cnn的越深層relu生成的圖片越抽象可能說明模型越希望保留更多語義信息?也是2017 ass3的作業,2024大概沒有,所以估計要把2017的Q3拿來做一做。
Style Transfer裡Texture Synthesis材質生成是個很老的CG問題,用一小塊圖片生成一大塊材質,傳統方法比如可以用nearest neighbour copy材質圖片。
後面十分鐘講Style Transfer和好看的圖片的內容就沒聽了,就聽到這裡outer product算gram matrix,聽不懂但是應該暫時不做2017年ass3的Q4,所以先不看,等做完2024年的ass3再做。
Lecture 13
- Unsupervised Learning
- Generative Models
- PixeIRNN and PixelCNN
- Variational Autoencoders (VAE)
- Generative Adversarial Networks (GAN)
Unsupervised Learning

Generative Models

生成模型的目標就是通過 $p_data$ 生成盡可能与 $p_data$ 相似的 $p_model$。即解決density estimation問題(無監督學習核心問題)。
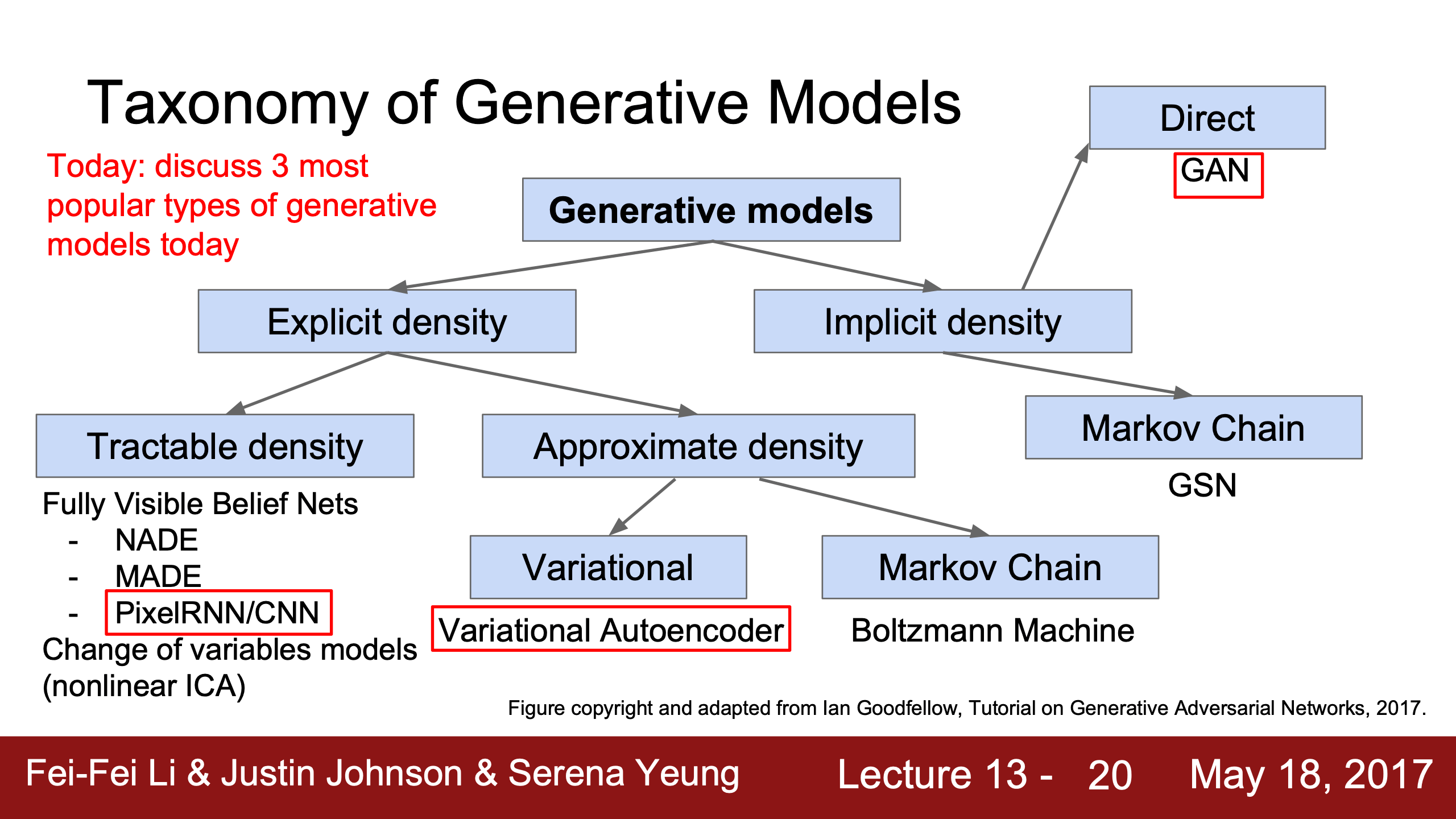
Density Estimation 密度估計,指的是通过已知数据点来估计一个数据分布的概率密度函数(PDF)。换句话说,密度估计旨在描述一个未知的分布,通常是通过从有限的观测数据中估计一个连续变量的分布形态。
PixelRNN/CNN
tractable Density (容易獲得的?)

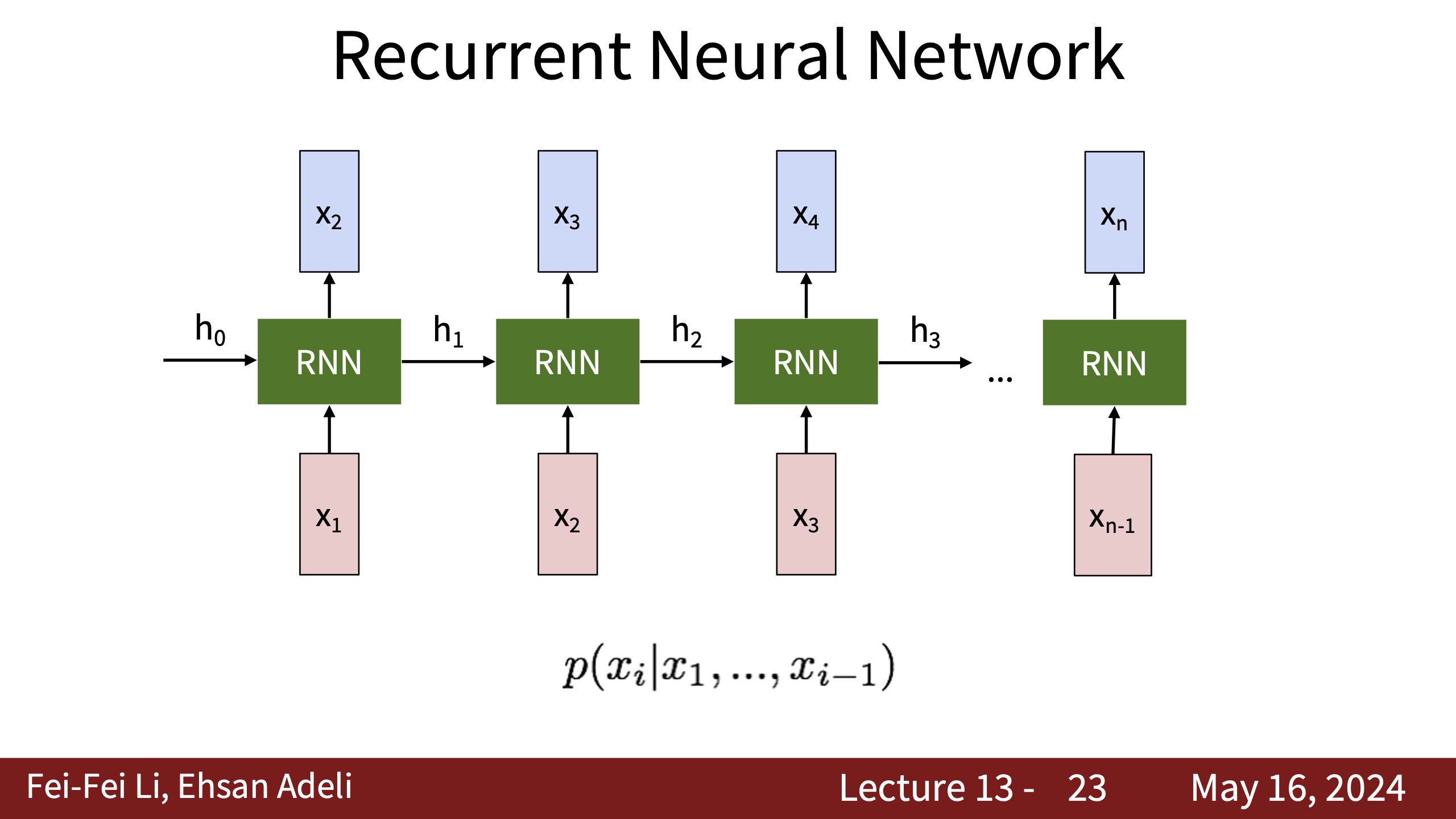

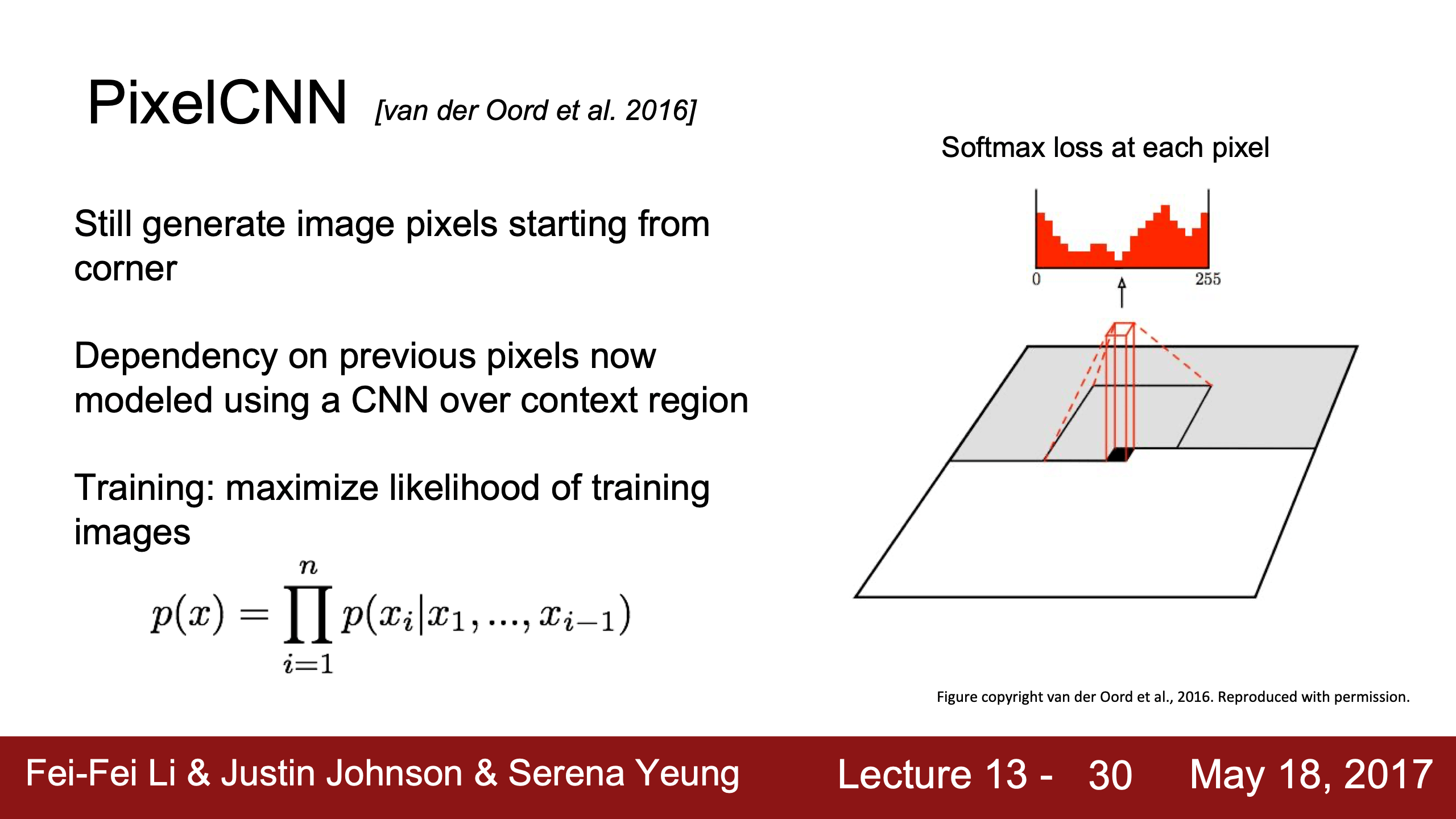

回顧似然likelihood,無監督學習中,尤其是generative models 生成模型們直接通过最大化似然来进行训练。
算法的label是training data本身,就是後續的像素,目標是最大化“訓練數據被生成”的似然。
Auto-Encoders
| 需要一個latent space z,而且因為我們希望z是最meaningful的features,z的維度要小於x也就是要先做dimensionality reduction。encoder和decoder可以用各種網絡構造 | 然後就出現了曾經我最熟悉的reconstruction loss也就是training data跟重建的自己做L2 loss,AE是通過重建自己的training data來學習z的。(另外熟悉的就是contrastive loss) | 我們可以利用學習到的 z 隱藏空間,在新的任務上 finetune |
|---|---|---|
 |
 |
 |
AE自编码器可以重建数据,并且能够学习特征以初始化监督学习模型。
但我们无法从自编码器生成新图像,因为我们不知道 $z$ 的空间,只是知道怎麼把 x 轉化到 z 空間。
VAE能让自编码器成为一个生成模型。VAE 會讓 z 輸出一個 $\mu$ 和 $\sigma$ 確定一個近似的正態分佈,然後可以在這個正態分佈裡採樣新樣本。
Variational Auto-Encoders
approximate Density
PixelCNN 定義的是 tractable 的公式,likelihood 裡的參數都是易得的:
VAEs 是定義了一個依賴於 latent z 的不能直接優化的公式,只是推導下面這個 likelihood 的 lower bound,然後轉而優化這個下界:
雖然在Elo裡詳細又學了一遍,但 ELBO (evidence lower bound) 或 variational lower bound 還是很難理解。
https://yunfanj.com/blog/2021/01/11/ELBO.html 這篇文章講得非常細緻,$p_\theta(x \mid z)$ 就是上面的 w (weights),核心思路是用多個Gaussian(或其他分佈)逼近目標分布。
总之先记住这个结论吧:
 |
 |
AE和VAE區別,KL散度作為正則
Generative Adversarial Networks
生成對抗網路。
總之生成任務都是試圖在高維的training data這個分布裡sample採樣,採樣出一些新的samples,這個分布是沒法直接得到的,AE/VAE是學習一個latent space z,通過“變分推斷”近似数据的真实分布。GAN是先從簡單分布比如Gaussian採樣,然後目標是變化這個分布(transformation)得到這個複雜分布。用Neural Network來學習這個“transformation”。VAE的neural network是被用來表示ELBO lowerbound的兩個似然?開始的思路是啥?其實這個學transformation的過程跟VAE變化prior的做法很像吧?

沃草,就是guest lecture 16 的lecturer Ian Goodfellow發的NIPS 2014 Generative Adversarial Nets。(他已經30w+引用了,guest lecture 15講硬件/加速的韓松也是個神人,6w+引用)
理解不能了,看到這裡還是一個似然,還是找幾個例子先想明白似然貝葉斯和nn的關係吧。
 |
 |
main idea是,我們訓練一個可以區分真假圖片的discriminator,如果generator可以生成出騙過discriminator的圖片,那麼可以說明generative model就已經足夠好了,這倆網絡是train jointly用一個minimax objective function。
GAN裡raining data的“real images”的label都是1,而generator生成的fake images的label都是0(unsupervised)。
 |
 |
Again,gradient ascent和gradient descent的唯一區別就是求出來梯度之後,前者加梯度後者減梯度。
但是看右下角的圖,$D(G)$ 越接近1(discriminator越把fake圖當成真的)即generator生成得越好的時候,$log(1-x)$ 曲線是越陡的,也就是說梯度是更大的,參數的變化是更快的,這是我們不希望的,我們希望 $D(G)$ 越接近0的時候參數更新越快,很巧妙的是可以把objective改成-log(x)(注意不是log(-x),這倆曲線前者是一四象限後者是二三象限)就有了這種好的 $D(G)$ 接近 0 時陡 $D(G)$ 接近 1 時緩的曲線,即gradient decent $-log(D(G))$,等價於gradient ascent $log(D(G))$。

訓練算法是,每個training iteration都先訓練k次discriminator,然後再訓練generator。這裡的k設成1還是大於1,直到2024年的slide還是跟2017年一樣,作為一個現調的超參沒人在乎了大概。
訓完就把discriminator丟掉用generator生成。這裡2014年Ian Goodfellow訓GAN的neural nets都是FC來的,但後來2016年Alex Radford用CNN訓了一套,效果變好了很多。
在早期GAN裡,是完全隨機地生成樣本,後來才有conditional cGAN允許用類別標籤、圖像、文本描述控制生成。
 |
 |
在latent space裡对隨機的z插值會有平滑的變化,是個有趣的實驗。對z做各種有趣的事看到圖像的合理變化能說明z有一定的可解釋性。
一個有趣的2-player IDEA,一個上口的名字 GAN,效果好就是大家爭相發展的硬道理。新的工作其實也只是修改一點兒loss function之類的工作,assignment 3裡2017和2024一直都有GAN(和RNN/LSTM)。
VAE相比GAN有inference queries:
大概就是VAE有個中間階段,encoder會生成一個latent space的mean和variance顯式得到分布,“decoder”採樣的過程就是明確的推理過程,可以比較方便地操作潛在變量;
而GAN沒有顯式推理過程,只用generator通過隨機噪聲生成樣本。
ass裡的兩個loss:BCE就是Binary Cross-Entropy Loss二分類交叉熵和Least Squares Loss (最小二乘损失),GAN原來同時可以用回歸和分類的損失。
Lecture 14

強化學習原來也是馬爾科夫過程,死去的LDA記憶又開始復蘇。
- What is Reinforcement Learning?
- Markov Decision Processes
- Q-Learning
- Policy Gradients
What is Reinforcement Learning?
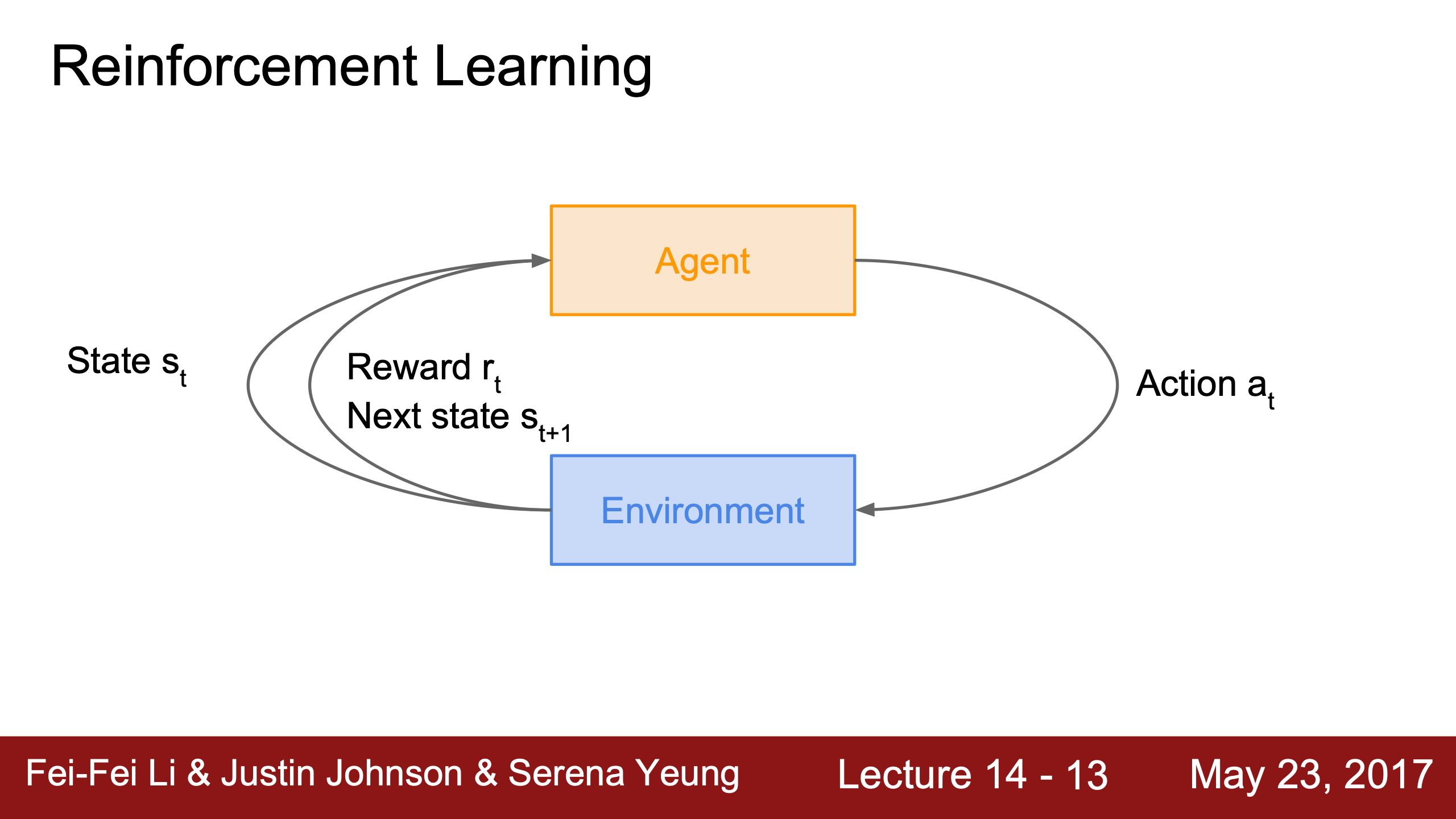
整個流程:
- Environment給Agent一個state
- loop:
- Agent給Environment一個action
- Environment給Agent一個reward和next state
- until Environment給Agent一個terminal state
cases:
- Cart-Pole Problem(推车摆问题)是一个经典的控制问题,通常用于强化学习(Reinforcement Learning, RL)和机器人学的研究中。这个问题描述了如何控制一个安装在推车上的摆杆(或倒立摆)保持直立的状态。它是一个经典的物理控制问题,具有挑战性,特别是在处理实时控制和系统稳定性时。
- Robot Locomotion(机器人运动学)優化運動方式、機器人穩定性。
- Games,比如 Go 圍棋、比如最早的遊戲公司 Atari。
Markov Decision Processes
 |
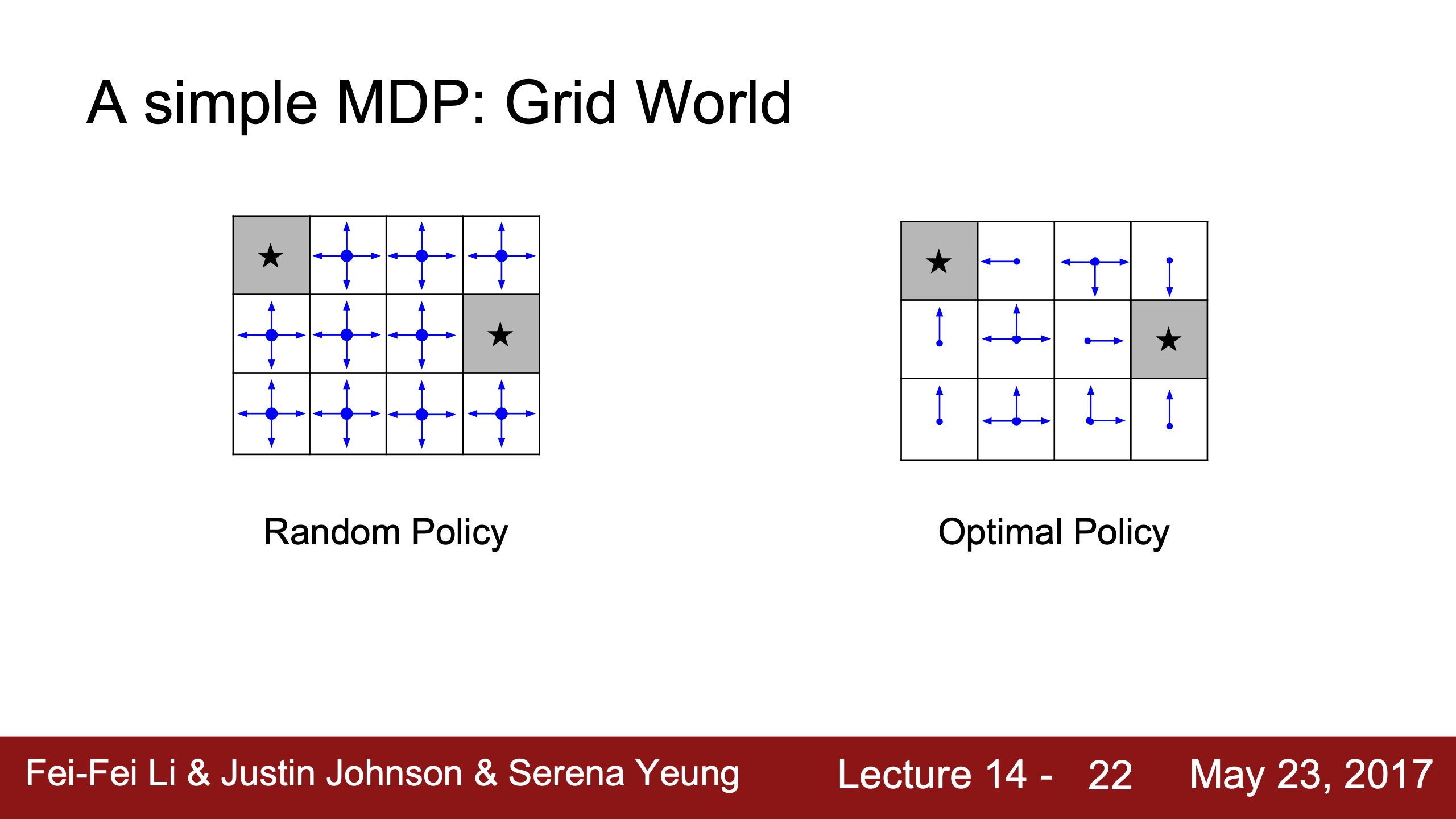 |
A Simple MDP: Grid World這個例子裡,reward被設為negative,就意味著到達終點越久cumulative reward累積獎勵就越小,policy pi的optimal應該是maximize the sum of rewards。
马尔可夫决策过程(MDP)是一个数学模型,又叫随机动态规划 (stochastic dynamic program), 通过五个元素 (或者4-tuple只有前四个)(状态、动作、转移概率、奖励函数、策略 / 折扣因子)M = (S, A, P, R, π / γ ) 描述智能体在环境中如何做出决策,以最大化长期奖励,其数学形式最早在 1950s 由 Richard Bellman 提出的动态规划理论奠定,并在 ecology, economics, healthcare, telecommunications and reinforcement learning 中广泛应用。
Q-Learning

Value Function(价值函数)
Value Function $V(s)$ 用于表示在状态 $s$ 下,智能体能期望获得的累积奖励。它通常定义为从某一状态出发,按照某个策略 $ \pi $ 行动所能获得的期望回报。
其中:
- $V(s)$: 在状态 $s$ 下的价值函数,表示从状态 $s$ 开始,按照某策略最大化累积奖励的期望值。
- $\mathbb{E}$: 期望操作符,表示对未来奖励进行期望计算。
- $\sum_{t=0}^{\infty}$: 求和符号,表示从时间步 $t=0$ 到无穷远的求和。
- $\gamma$: 折扣因子,$0 \leq \gamma < 1$,用于降低未来奖励的重要性。
- $r_t$: 时间步 $t$ 时的奖励。
- $s_0$: 初始状态,表示从状态 $s$ 开始进行决策。
Q-Value Function(Q值函数)
Q值函数 $Q(s, a)$ 用于表示在某个状态 $s$ 下,采取某个动作 $a$ 后能获得的期望累积奖励。Q值函数是强化学习中非常关键的函数,常用于评估特定的动作选择。
其中:
- $Q(s, a)$: 在状态 $s$ 下,采取动作 $a$ 后的 Q 值,表示从状态 $s$ 出发并采取动作 $a$ 后能期望获得的累积奖励。
- $\mathbb{E}$: 期望操作符,表示对未来奖励进行期望计算。
- $\sum_{t=0}^{\infty}$: 求和符号,表示从时间步 $t=0$ 到无穷远的求和。
- $\gamma$: 折扣因子,$0 \leq \gamma < 1$,用于降低未来奖励的重要性。
- $r_t$: 时间步 $t$ 时的奖励。
- $s_0$: 初始状态,表示从状态 $s$ 开始进行决策。
- $a_0$: 初始动作,表示在状态 $s$ 下采取的动作。
| Bellman equation 是 loss function | 用 nn 作為函數逼近來估計所有 state-action pair 的 Q(s,a) |
|---|---|
 |
 |
但是這樣一個個試錯的做法not scalable,面對大規模數據沒有擴展性,計算開銷太大,
而一旦出現一個很複雜的function比如Q(s,a)就是這樣一個function,我們想估計,就可以用neural nets作為函數逼近器(function approximator)來用數值方法逼近這個函數。
$Q(s,a;\theta) ~ Q^*(s, a)$
網絡的輸入就是 s 和 a,輸出就是Q(s, a),思路很直接,但是就像2019年亞太杯一樣,問題是:
- loss function
- model structure
- 實現後找問題
這裡倆問題,1.reward怎麼來?人為設定的,比如Atari的打磚塊遊戲breakout,打掉一個磚塊+1,球掉了-1,或者可以設置成0;2.貼過來pseudo代碼?跟上面公式不太一樣?
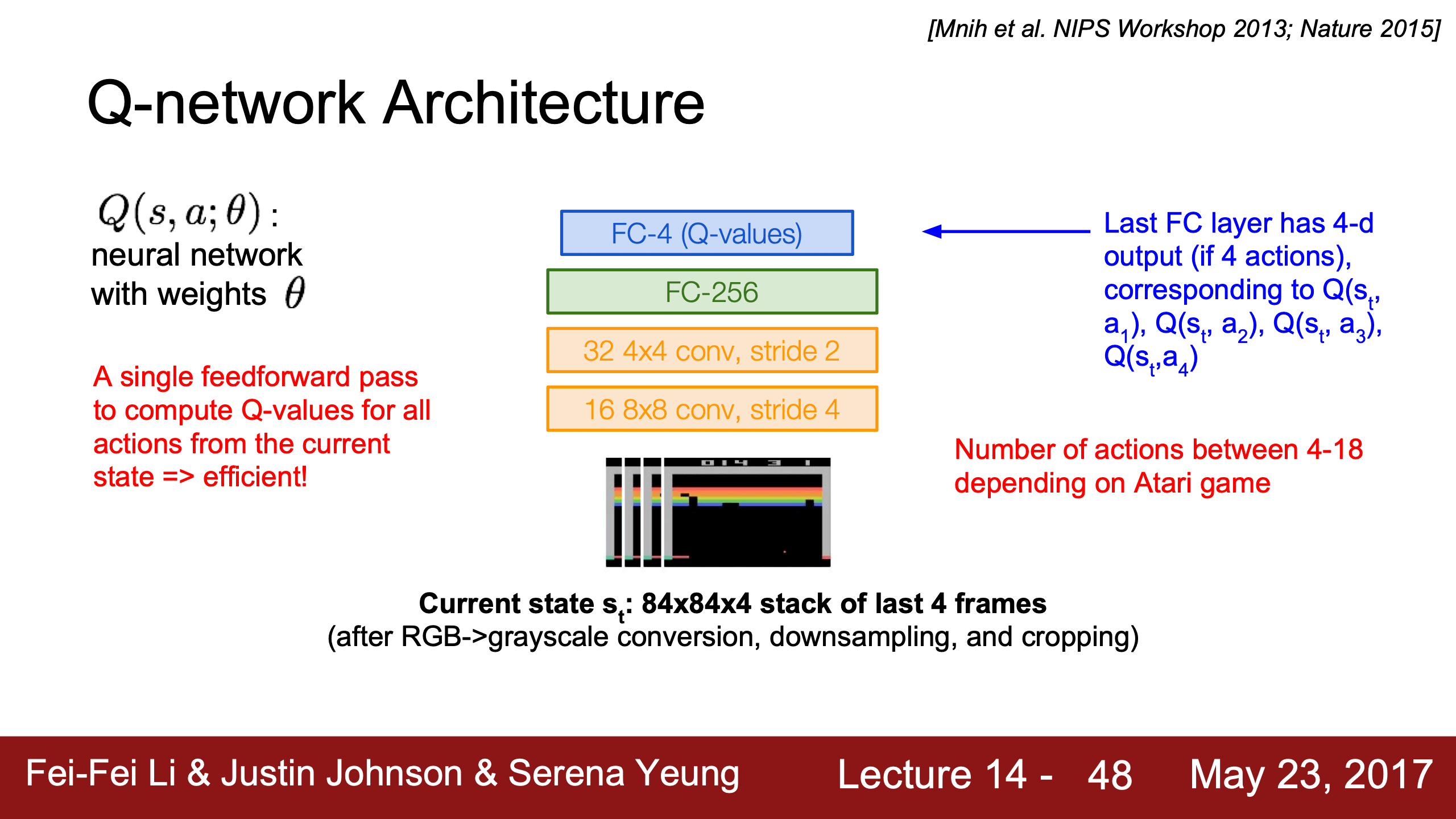
Input: state $s_t$
訓一個atari像google那樣?為什麼nn能有這麼高效率算出來Q?
傳統 Q-learning
Q-Learning 更新公式
Q-learning 是一种无模型的强化学习算法,即Agent不需要知道环境的具体模型(即状态转移概率state transition probability和奖励函数reward function),只通过与环境的交互来逐渐学习最优策略。通过与环境的交互,不断更新 Q-值函数。其核心更新公式如下:
其中:
- $Q(s_t, a_t)$: 当前时刻 $t$,在状态 $s_t$ 下采取动作 $a_t$ 的 Q 值,表示预期的累积奖励。
- $\alpha$: 学习率,决定了每次更新的幅度,$0 \leq \alpha \leq 1$。
- $r_{t+1}$: 在时刻 $t+1$ 获取的奖励。
- $\gamma$: 折扣因子,$0 \leq \gamma < 1$,用于降低未来奖励的重要性。
- $\max_a Q(s_{t+1}, a)$: 在下一个状态 $s_{t+1}$ 中,所有可能的动作 $a$ 中,具有最大 Q 值的动作对应的 Q 值。
- a是“最大Q值的動作”。
- $s_t$: 当前时刻 $t$ 的状态。
- $a_t$: 当前时刻 $t$ 选择的动作。
在訓練階段是有時隨機地隨意地、有時用maxQ轉移狀態探索環境來更新Q矩陣,
在決策階段就用Q值貪心地選擇最優策略 $a^*(s) = \arg\max_a Q(s, a)$。
直觀地理解Q-Learning更新公式的Intuition:
- $Q(s_t, a_t)$ 表示的是從 $s_t$ 這個狀態通過 $a_t$ 這個行動轉移到下個狀態的價值、回報;
- 因為是在學習,首先更新這個值就要加上原來的學習經驗 $Q(s_t, a_t)$(沒有經驗初始化為0);
- $\alpha$ 就相當於學習率,不用管;
- $\left[ r_{t+1} + \gamma \max_a Q(s_{t+1}, a) - Q(s_t, a_t) \right]$ 是更新的部分,包含 $r_{t+1}$、$\gamma \max_a Q(s_{t+1}, a)$、$- Q(s_t, a_t)$;
- $r_{t+1}$ 即時獎勵是 $Q(s_t, a_t)$ 轉移狀態探測環境後實際獲得的獎勵,這是環境給的;
- $\max_a Q(s_{t+1}, a)$ 是未來獎勵的預期,這一步的價值不光包括立刻獲得的獎勵,還要往下一步看看最大能獲得多少獎勵,即多看一步的貪心算法,$\gamma$ 是給未來預期打個折扣;
- $- Q(s_t, a_t)$ 是為了避免過度更新減掉的,因為 $r_{t+1} + \gamma \max_a Q(s_{t+1}, a)$ 是实际获得的即时奖励 + 未来可能的回报,加太多不減點兒會導致Q值起飛數值不穩定。
更新公式的核心是时序差分(Temporal Difference, TD)方法,實際是蒙特卡洛方法和動態規劃思想的結合。又叫Bellman Error又叫Temporal Difference,有空再研究推導,Serena這裡公式一筆帶過了算是課外內容。
傳統 Q-learning 是維護一個 Q(s, a) 表(所謂時序差分裡面動態規劃思想的部分),用 $Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha \left[ r_{t+1} + \gamma \max_a Q(s_{t+1}, a) - Q(s_t, a_t) \right]$ 公式更新表(所謂時序差分裡面蒙特卡洛思想的部分)。
而 DQN 是輸入 s 直接由 nn 回歸得到 Q 值。
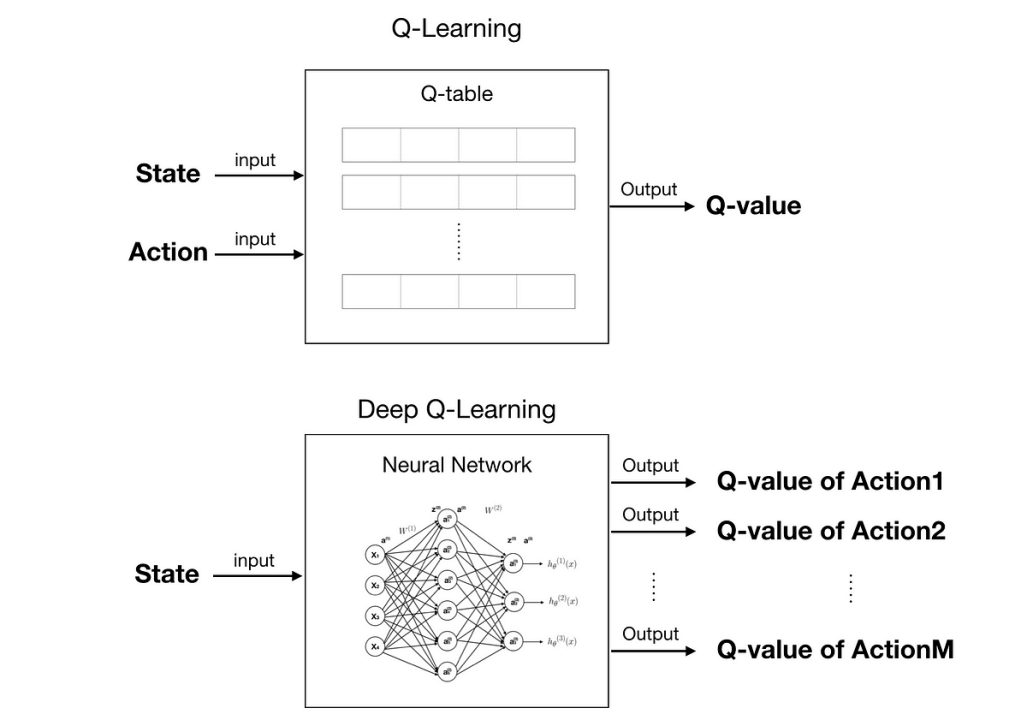
↑ 傳統 vs. Deep ↑
DQN, Deep Q-Learning
輸入:環境 Environment 的狀態 State $s_t$ ,可以是一個向量(比如迷宮用FC)、圖像(比如Atari games用Conv)或其他特徵。
輸出:一個向量 vector,表示所有可能動作 Action 對應的 Q-value。
網絡架構跟其他任務沒什麼兩樣。相當於把填表工作交給數值逼近高手神經網絡。

Loss function: $L_i\left(\theta_i\right)=\mathbb{E}_{s, a \sim \rho(\cdot)}\left[\left(y_i-Q\left(s, a ; \theta_i\right)\right)^2\right]$ where $\quad y_i=\mathbb{E}_{s^{\prime} \sim \mathcal{E}}\left[r+\gamma \max _{a^{\prime}} Q\left(s^{\prime}, a^{\prime} ; \theta_{i-1}\right) \mid s, a\right]$
- 這個 loss 是 Bellman 誤差 (Bellman error) 最小化,最小化當前 Q 函數 $Q(s, a; \theta_i)$ 和目標值 $y_i$ 。
- $y_i$ 代表的是當前 Q 函數即 $Q(…; \theta_{i-1})$ 在下一個狀態 $s’$ 中最理想的 rewards 最大的可能性;
- 可以發現 loss 裡的 $y_i$ 基本就是更新公式 $Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha \left[ r_{t+1} + \gamma \max_a Q(s_{t+1}, a) - Q(s_t, a_t) \right]$;
- 這個是理想值,用一個神經網絡縮小它跟 $Q(s, a; \theta_i)$ 的差距以學到更好的 Q(s, a);
- $y_i$ 是不斷改變隨 Q(s, a) 更新的!
- $Q(s, a; \theta_i)$ 和 $Q(…; \theta_{i-1})$ 都是由神經網絡預測。
Policy
這個 loss 公式裡有兩個沒說明的點,
- $\rho(\cdot)$ 是個分布函數,是個行為策略 (Behavior Policy,通常寫作 $\rho$ ),所謂行為策略就是訓練時用的策略,是被優化的目標,最終目標叫做目標策略 (Target Policy,通常寫作 $\pi$ ),行為策略和目標策略又可以分為以下幾種:
- 策略 policy 就是在某state下應該執行哪個action,比如在一個 action 只有上下左右的迷宮裡用均勻分布隨機策略,$\rho(s, a_1) = 0.25, \quad \rho(s, a_2) = 0.25, \quad \rho(s, a_3) = 0.25, \quad \rho(s, a_4) = 0.25$ 或 $\pi(s, a_1) = 0.25, \quad \pi(s, a_2) = 0.25, \quad \pi(s, a_3) = 0.25, \quad \pi(s, a_4) = 0.25$,每種。
- 确定性策略(Deterministic Policy):s下就執行a,$\pi(s) = a$,一個狀態就對應一個行為;
- 随机策略(Stochastic Policy):策略給一個概率分佈,$\pi(a \mid s) = P(a \mid s)$ 狀態s下執行動作a0的概率是0.8,執行動作a1的概率是0.2。
- 貪婪策略 (Greedy Policy):$ \pi_{\text{greedy}}(a|s)$ 代表狀態 s 下選擇動作 a 的概率,即只會選擇讓 Q(s, a) 最大的 a’。
- ε-贪婪策略(ε-greedy Policy):假設 ϵ 設置為 10%,意味著有 10% 時間裡會進行探索。 意思是有 90% 機率選擇讓 Q(s, a) 最大的 a’,剩下的所有動作 a 都有均等概率被執行。
- 注意⚠️,上面公式裡的 $\pi$ 都可以改成 $\rho$,也就是說這些策略既可以作為訓練用,又可以用來實際推理用;
- 如果一個算法裡 $\pi$ 和 $\rho$ 選擇的策略一樣,比如都是貪婪策略,這種就叫 on-policy 強化學習;
- 如果 $\pi$ 和 $\rho$ 不一樣,比如 Q-learning,訓練時用ε-贪婪策略保持探索性,推理時用貪婪策略每一步都選收益 Q(s, a) 最大的 a,這就叫 off-policy 強化學習。
- 最後,↓ 經驗回放(Experience Replay) ↓,壓軸策略。
- $\mathcal{E}$ 是經驗回放策略維護的 經驗回放池(Replay Buffer),是 Agent 和 Environment 交互的所有經驗,這麼講有點抽象,其實就是統計每個 state 選了什麼 action 對應了什麼 reward,舉個例子:
- 假設現在狀態空間是 5x5 的網格,Agent 從 (0, 0) 開始移動,終點是 (4, 4) 。
- 假如已經交互了一百次,現在又回到了 (0, 0) 每次的經驗是下面這樣——
| Episode | 状态 (S) | 动作 (A) | 奖励 (R) |
|---|---|---|---|
| 1 | (0,0) | 向右 | +1 |
| 2 | (0,0) | 向右 | +1 |
| 3 | (0,0) | 向下 | +2 |
| 4 | (1,0) | 向右 | +1 |
| 5 | (1,0) | 向下 | +2 |
| 6 | (1,1) | 向右 | +1 |
| 7 | (1,1) | 向右 | +1 |
| 8 | (2,1) | 向下 | +2 |
| 9 | (2,2) | 向右 | +1 |
| 10 | (3,2) | 向右 | +1 |
| … | … | … | … |
那麼現在在(0, 0),假如:
- 在
(0, 0)状态下,“向右”动作执行了 30 次,平均奖励为 +1。 - 在
(0, 0)状态下,“向下”动作执行了 20 次,平均奖励为 +2。
在经验分布策略中,Agent 会根据每个动作的历史表现(即其平均奖励)来调整选择该 Action 的概率。通常,代理会根据每个动作的优势(奖励)和执行次数来评估选择概率。
方法1: reward 和執行次數算 weighted sum
计算每个动作的总奖励:
- 对于“向右”动作,执行了 30 次,平均奖励 +1,因此总奖励是:
$30 \times 1 = 30$ - 对于“向下”动作,执行了 20 次,平均奖励 +2,因此总奖励是:
$20 \times 2 = 40$
- 对于“向右”动作,执行了 30 次,平均奖励 +1,因此总奖励是:
计算每个动作的选择概率:
- 总奖励:$30 + 40 = 70$(即两种动作的总奖励)。
- “向右”的选择概率是:
$P(\text{向右}) = \frac{30}{70} = 0.4286$ - “向下”的选择概率是:
$P(\text{向下}) = \frac{40}{70} = 0.5714$
更常用方法2: 优势函数
- advantage function:
- 算基準獎勵,假設是總獎勵平均值 $\frac{30 \times 1 + 20 \times 2}{30 + 20} = \frac{30 + 40}{50} = 1.4$,
- 算優勢 advantage = 平均獎勵 - 基準獎勵。
- 優勢:$A(\text{向右}) = 1 - 1.4 = -0.4$,$A(\text{向下}) = 2 - 1.4 = +0.6$。
- softmax $P(\text{动作}) = \frac{e^{A(\text{动作})}}{\sum_{\text{动作}} e^{A(\text{动作})}}$

每種策略生成的 Q-value function Q(s, a) 是不同的,Q值依賴於 Agent 所使用的策略。
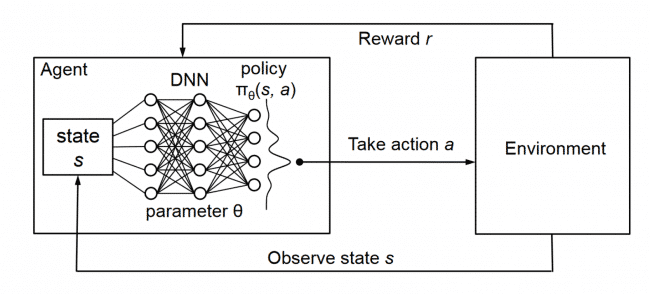
↑ 根據模型輸出的 Q(s, a) 和採用的 policy 公式,生成一個概率分佈選擇 action。↑
Continue Lecture 14 Reinforcement Learning
Policy Gradients
問題是Q,這個value of state action pair會非常非常非常大,比如圖裡的高維問題。
Q很大(情況很多)但是決策一般比較簡單,所以是否可以從collection of polices裡直接學到一個policy?(這裡的 policy 就是上面 Q-learning 討論的)

這個公式跟 Value Function 一模一樣,只把 given $s_0$ 改為 given $\pi_\theta$。
代表算法 ↓
REINFORCE algorithm
| 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
 |
 |
 |
 |
 |
- 每個 $\pi_\theta$ 都有很多可能路徑 trajectory $\tau$,期望展開,就是每個軌跡的 reward 和軌跡概率分佈的積分。
- $\nabla_\theta J(\theta) = \int_{\tau} r(\tau) \nabla_\theta p(\tau; \theta) \, d\tau$ 被積函數光滑可微時,梯度和積分就可以互換,根據某些法則。
- trick 是 log(x) 導數 = 1/x;
- $\begin{aligned} \nabla_\theta J(\theta) & =\int_\tau\left(r(\tau) \nabla_\theta \log p(\tau ; \theta)\right) p(\tau ; \theta) \mathrm{d} \tau \\ & =\mathbb{E}_{\tau \sim p(\tau ; \theta)}\left[r(\tau) \nabla_\theta \log p(\tau ; \theta)\right]\end{aligned}$
- 這個公式還是期望展開成積分,反過來積分倒回期望。
- 直接計算這個期望可能非常困難,因為我們無法遍歷所有可能的路徑 $\tau$。但根據大數法則,我們知道,如果我們從分佈 $p(\tau; \theta)$ 中抽取足夠多的樣本 $\tau_1, \tau_2, \dots, \tau_N$,那麼這個期望可以通過樣本的平均來近似:這就是蒙特卡洛方法的核心。它依賴於從分佈 $p(\tau; \theta)$ 中抽取的隨機樣本來近似整個期望值。我們通過多次採樣從策略分佈中獲取不同的路徑 $\tau_i$,對每個樣本計算其相應的回報 $r(\tau_i)$ 和策略梯度 $\nabla_\theta \log p(\tau_i; \theta)$,然後求取平均來估計期望。
- transition 就是 $(s_t, a_t, r_t, s_{t+1})$ 四元組,這裡的技巧就是log累乘變累加。
- 最終求出梯度的直覺就是,$reward(\tau)$ 越大,$\pi(a_t|s_t)$ 越變大,即在 $s_t$ 下根據 policy 採用 $a_t$ 動作的概率就直接變大。
- 路徑裡每個行動的短期 reward 方差很大,比如隨機性影響,明明很好的一步但是天氣很差,明明很差的一步但是對手很弱,所以要關注長期影響,改成不不只關注時間 t 的當下回報 $r_t(\tau)$,關注從當前時間步開始未來的累積回報,但是很容意想到,如果 reward 都是正的,idea 1 和 2 會不停地把 action 們的 probability 拉高,所以可以減一個目前為止的平均值,作為 baseline。
| vanilla | |
|---|---|
 |
 |
| 然後發現這倆值正好就是 Q 和 V | 這個新算法正好就是experience replay裡的advantage |
|---|---|
 |
 |
在八方城那個出租屋裡,老闆半夜十一點半給我打電話說別學LDA學點有用的,沒想到強化學習也需要蒙特卡洛採樣,模擬估計值(狀態價值,動作價值)。好吧發現記錯了,這裡不是 Markov chain Monte Carlo MCMC 。
正好是这节课的前一天柯洁输了AlphaGO第一场比赛。
发现 stable-baseline3 这个宝藏 repo,直接跑个 Atari Game 玩玩看。
Lecture 15
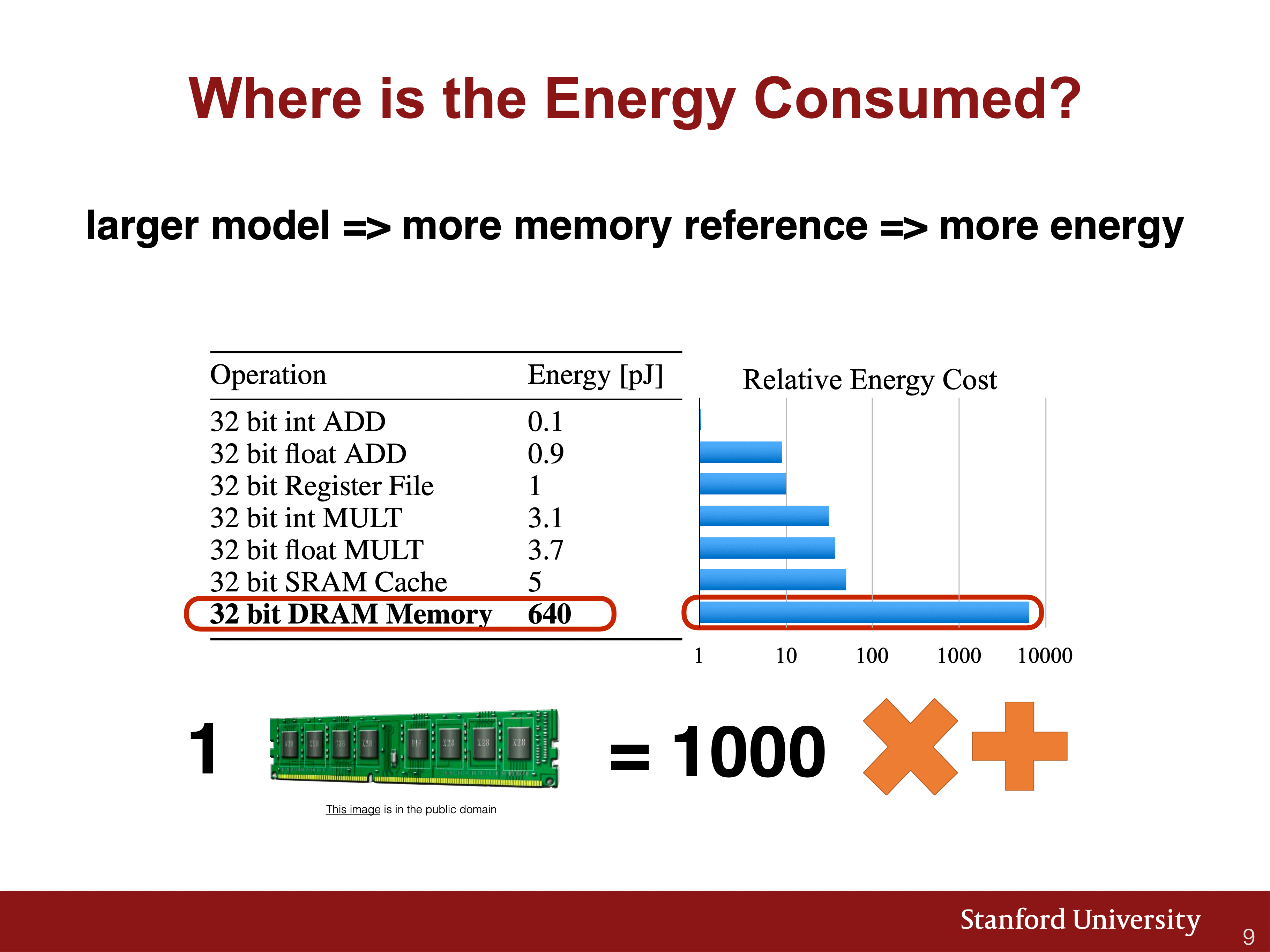
最耗電的是內存操作。
pJ 是 皮焦耳(picojoule)能量单位的缩写。它是焦耳(J,joule)的子单位。1 pJ = 10⁻¹² J。
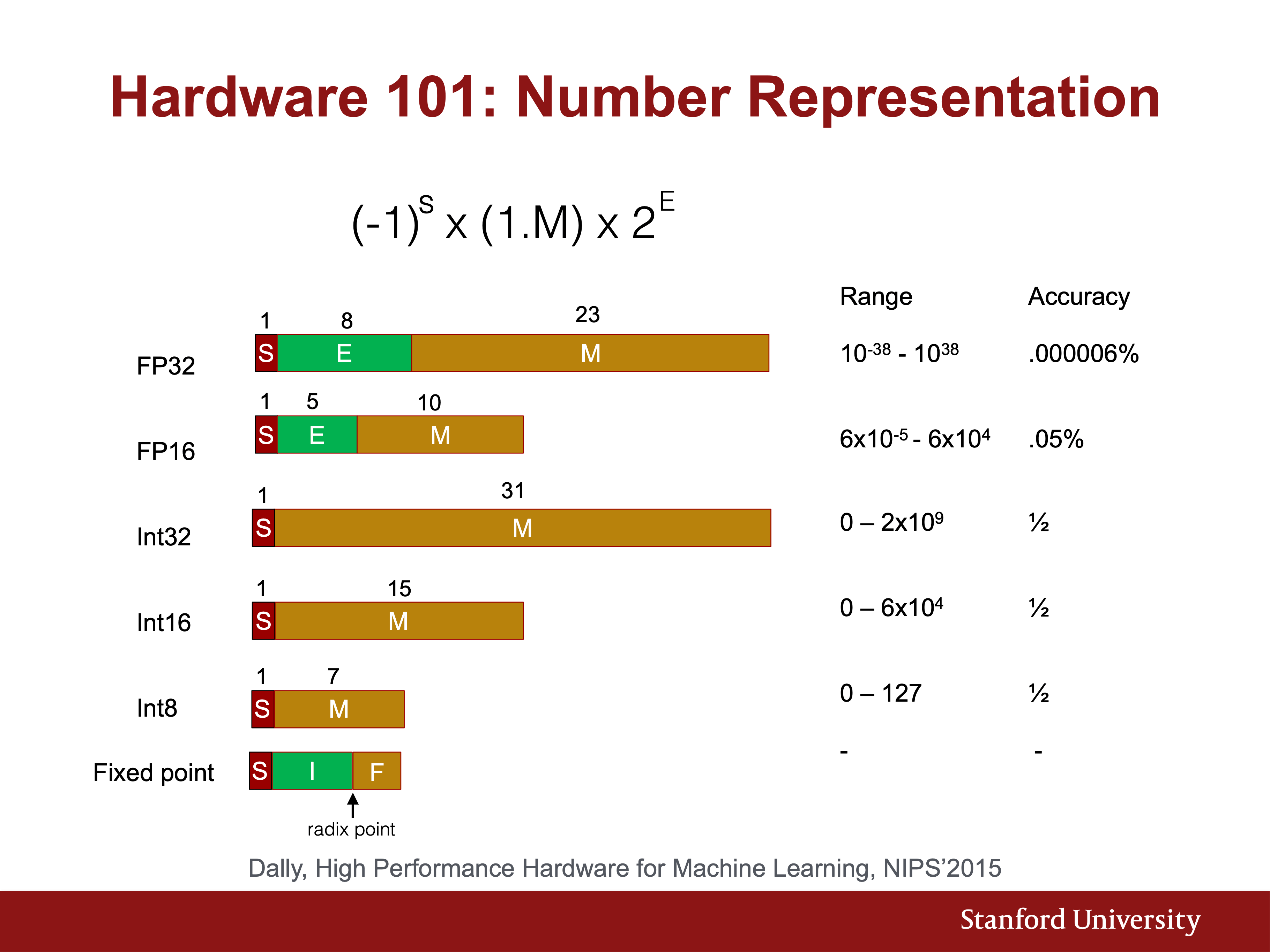
各種數據類型。
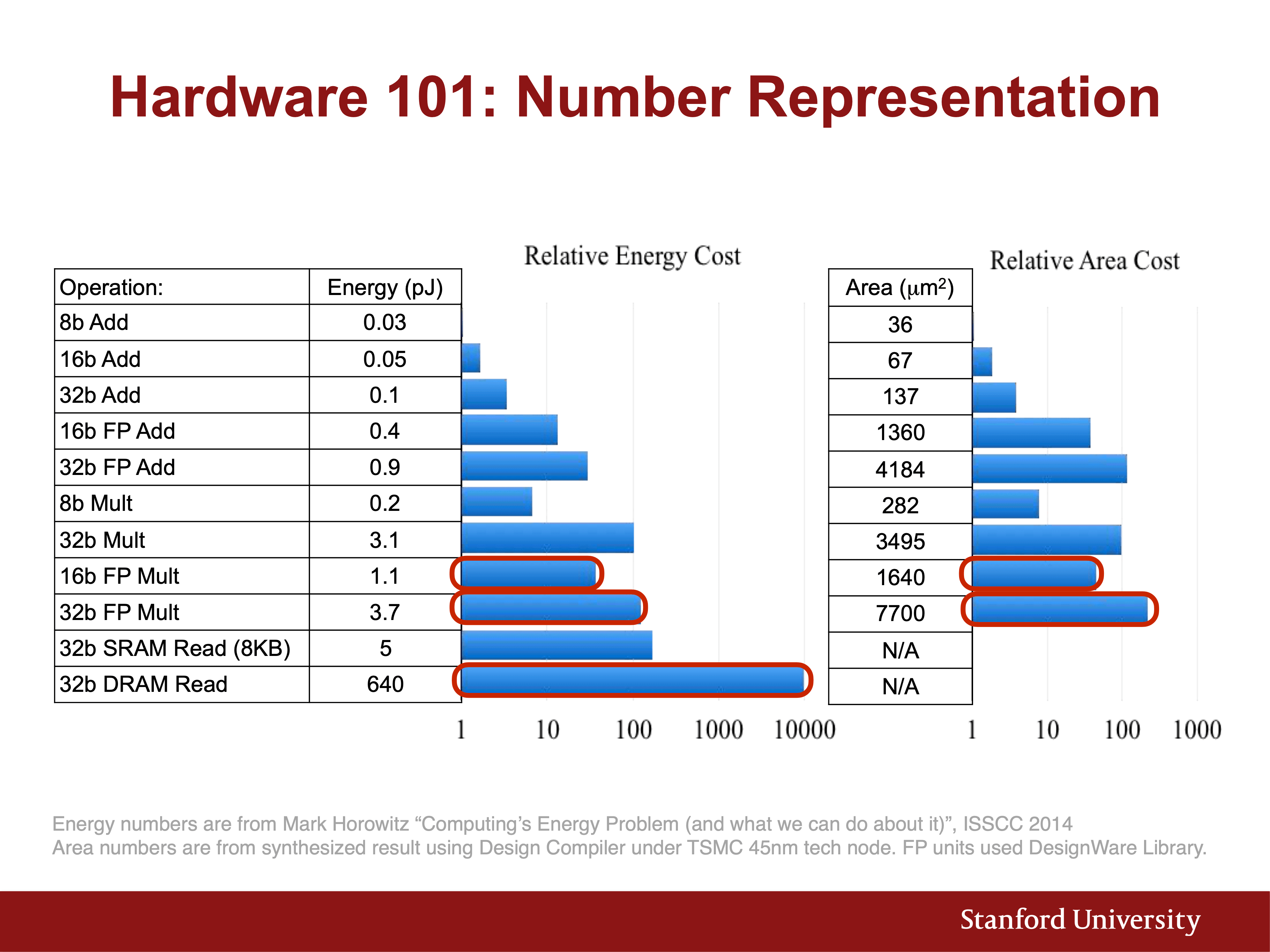
浮點乘是最占芯片空間的操作,DRAM讀取是最耗電的。
RAM 随机存取存储器:
SRAM (Static RAM) 使用一组反向的晶体管来存储每一位数据(通常是 4-6 个晶体管),常用於 Cache。
DRAM (Dynamic RAM) 使用一个晶体管和一个电容器来存储每一位数据。数据存储在电容中,但由于电容会逐渐放电,因此 DRAM 必须定期刷新(每几毫秒刷新一次)以保持数据。
Algorithms for Efficient Inference
- Pruning
- Weight Sharing
- Quantization
- Low Rank Approximation
- Binary / Ternary Net
- Winograd Transformation
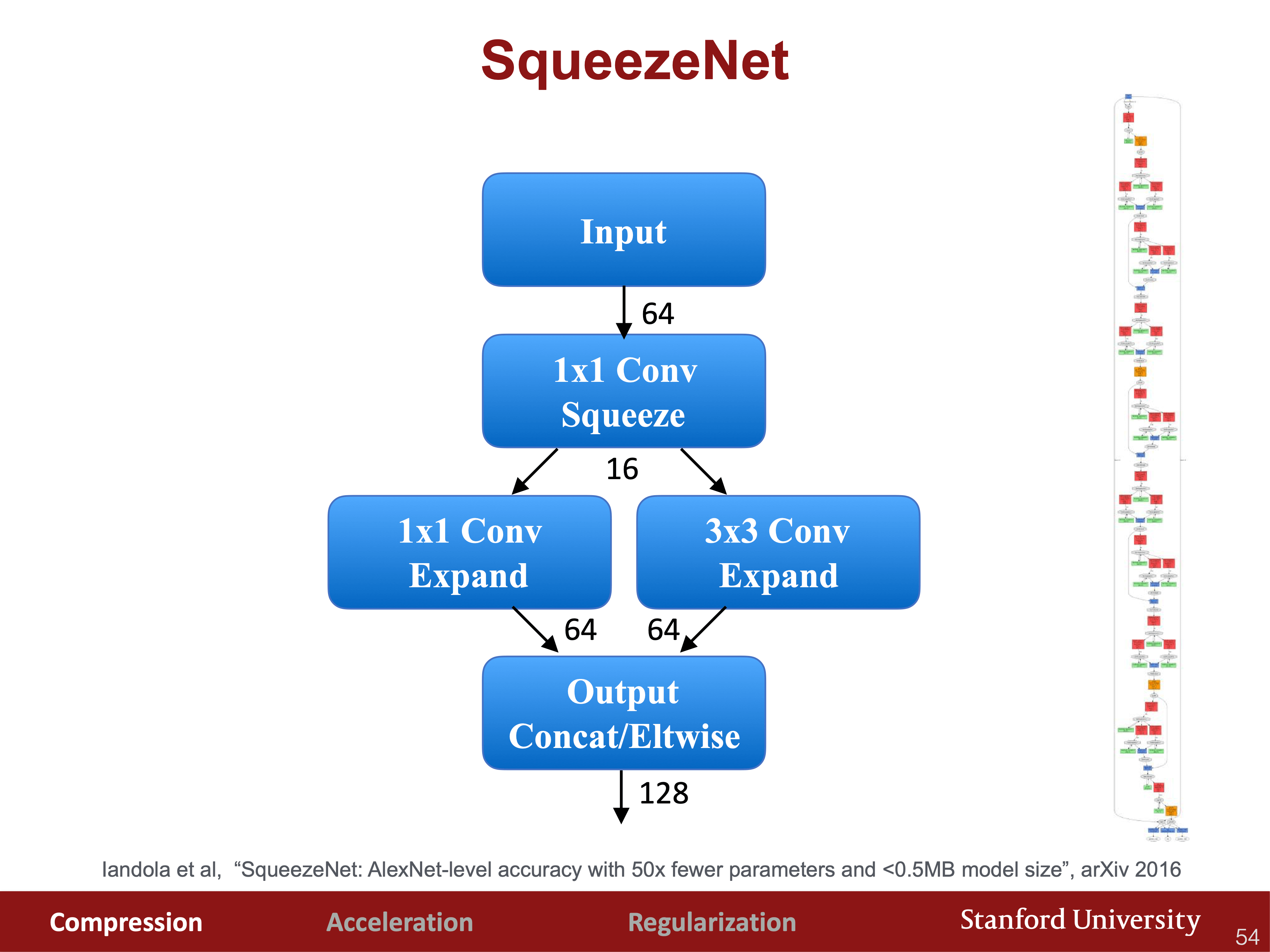
之前cnn architectures部分提到過可以先用1x1 conv減少input維度可以大大節省運算開銷。
Pruning
- Weight Pruning
- Neuron Pruning
方法就是直接把 weight 或者 activation 置 0。
- 根據 weight 絕對值大小,低於 threshold 的置0。
- 根據 neuron 被激活比例,即有多少是在activation function的有效區間裡。
- 根據梯度。
 |
 |
Weight Sharing
把所有 weights 都取整,只存索引。
 |
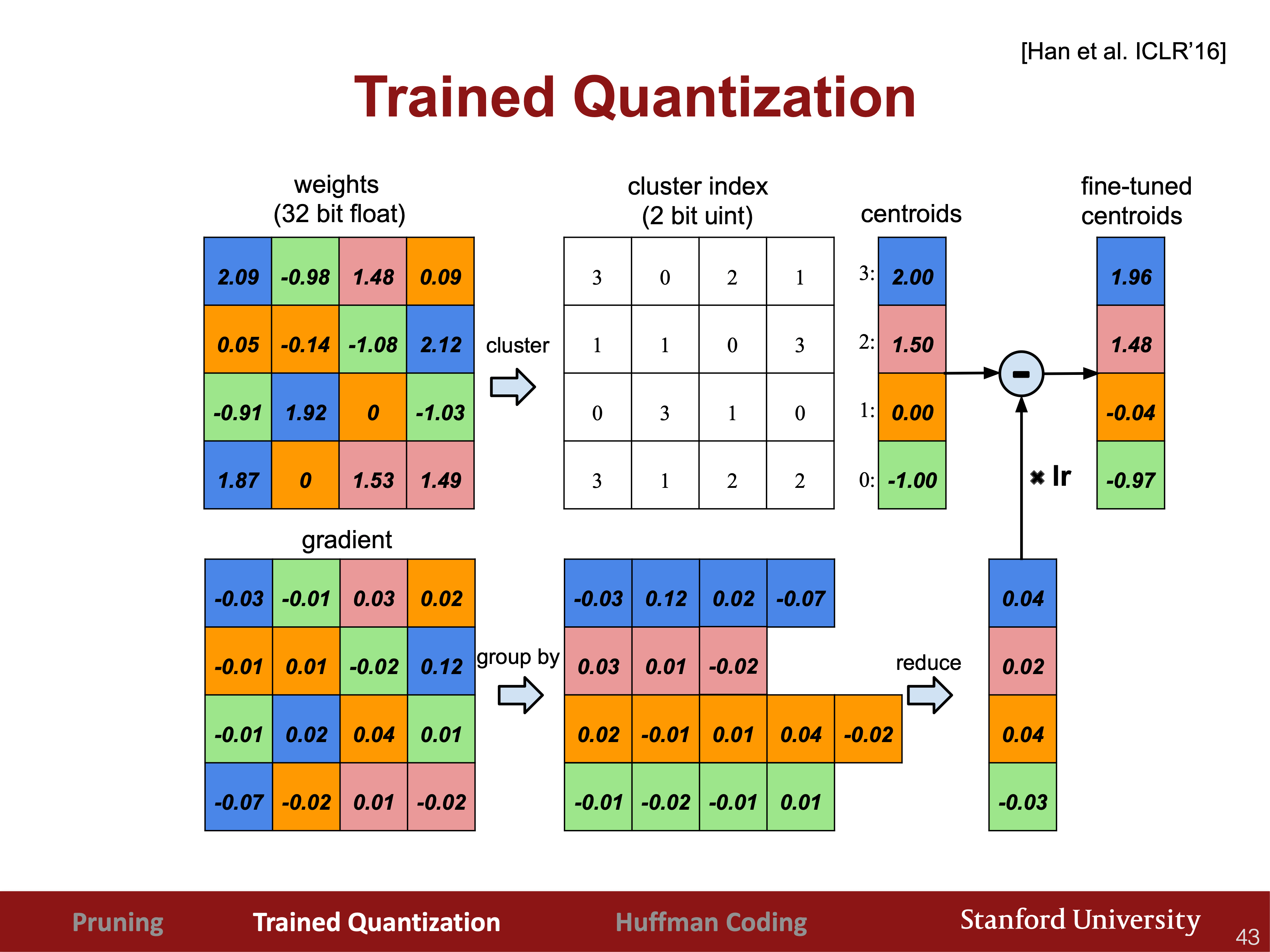 |
Quantization
就是把小的浮點數擴大(線性縮放scale)到整數。
- weight quantization
- activation quantization
權重和激活值量化是一樣的方法。舉個例子:
权重量化
假设某一层的权重矩阵是浮动的:
你可以使用 线性量化 进行转化,即定义一个量化比例(scale),例如,假设我们选择将权重范围映射到 8 位整数范围 [0, 255]。假设最大值为 1.0,最小值为 -1.0,量化尺度(scale)为:
将权重乘以量化比例,得到量化后的整数值:
计算结果为:
然后,你可以用这些整数权重值进行神经网络的推理。
激活量化
假设神经网络的某一层的激活输出为:
你可以对这些激活值进行量化,将它们映射到一个整数范围,比如 [0, 255],并进行类似的操作来获得量化后的激活值。
假设最大值为 1.0,最小值为 -1.0,量化尺度(scale)为 127.5,那么激活的量化过程是:
计算结果为:
擴大後再 round 捨掉的精度會小兩三個量級。
這也是TPU為什麼能用INT8的原因。既節省空間又提高速度。
Low Rank Approximation
低秩近似,用奇异值分解(SVD)之類的矩陣分解技術把卷積核分解。
Binary / Ternary Net
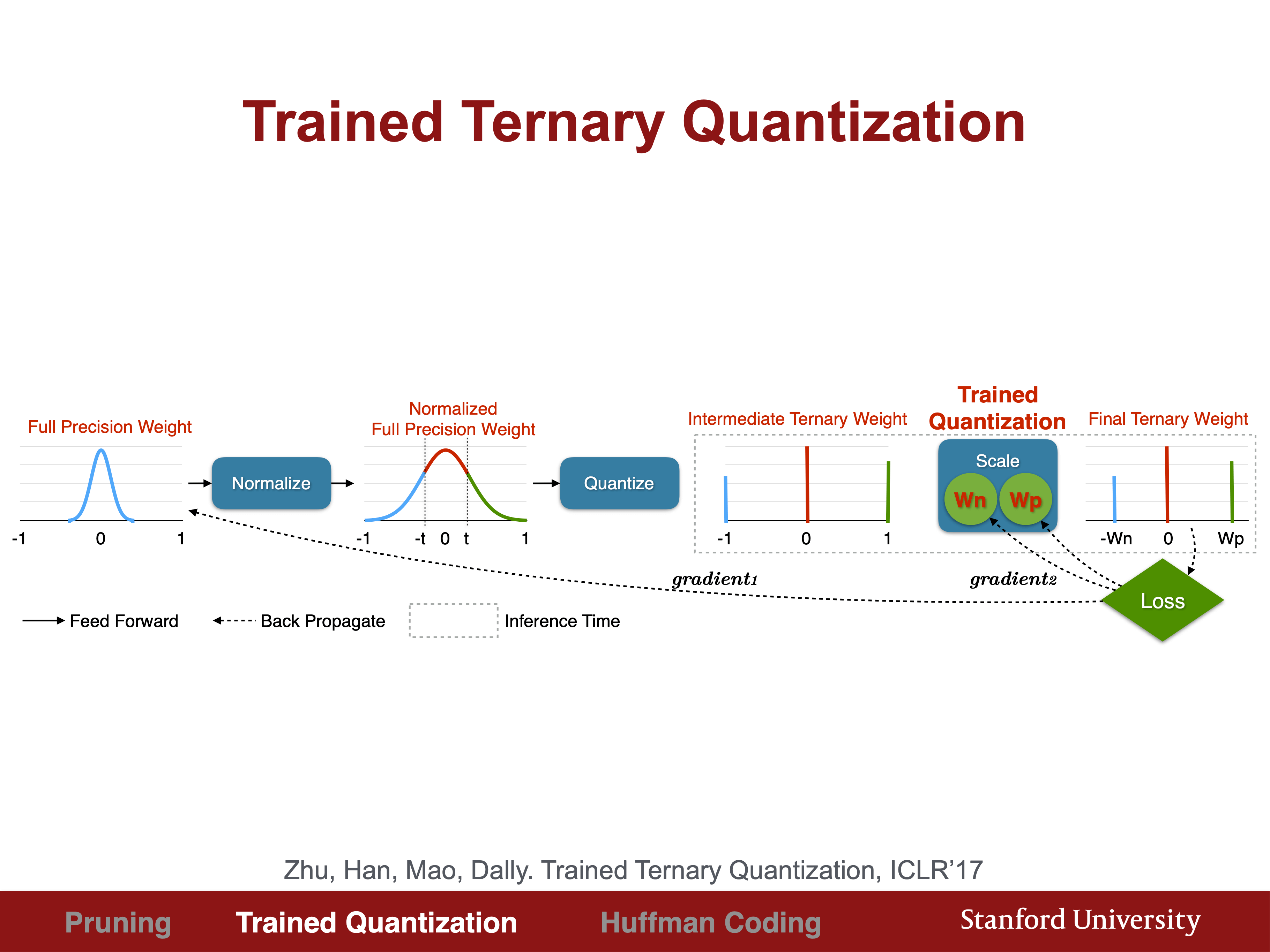
大道至簡,直接給所有weight簡化成2個或3個值。
Winograd Transformation
通過Winograd算法能減少卷積裡的乘法次數。
Hardware for Efficient Inference
a common goal: minimize memory access
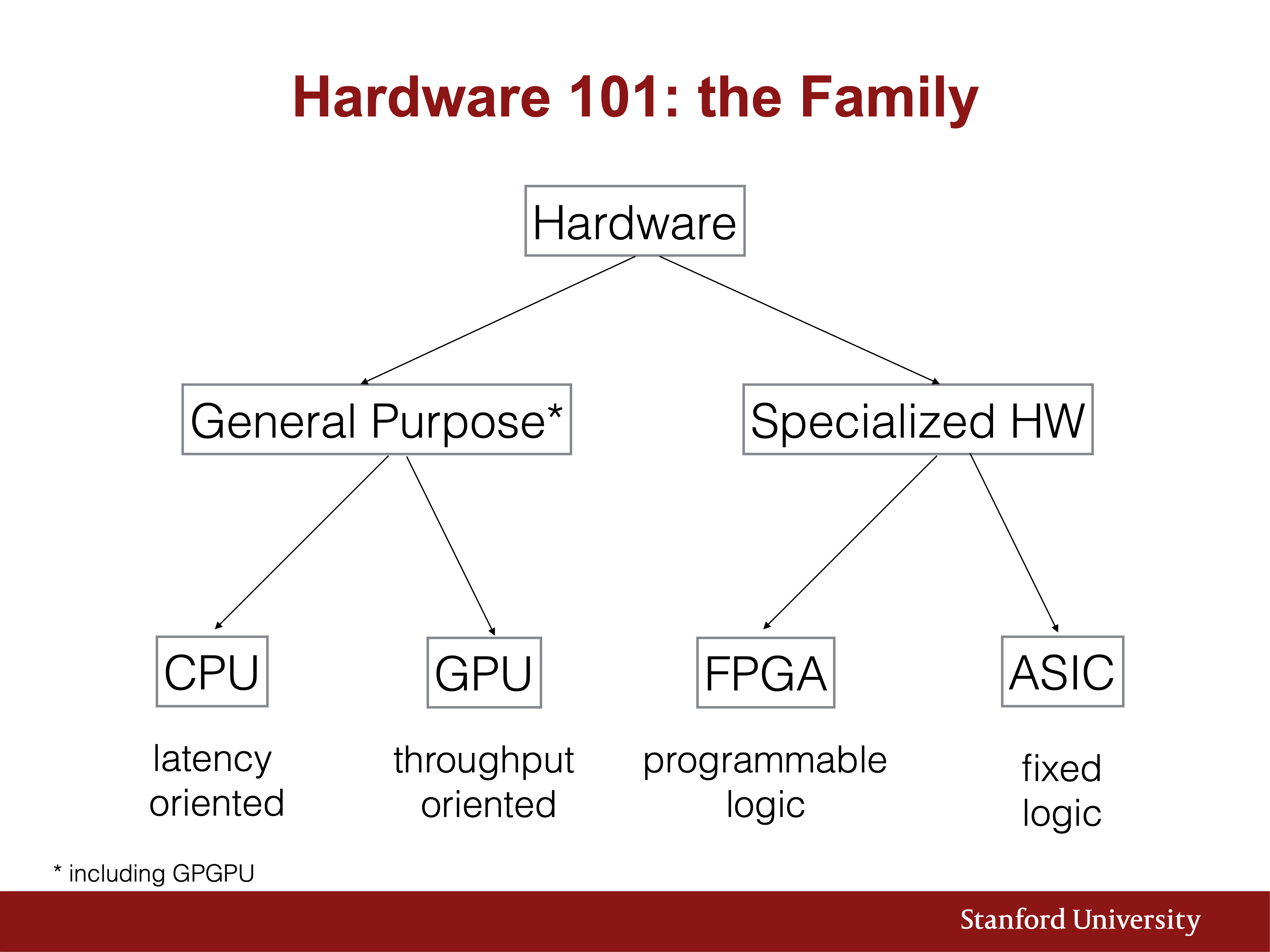
ASIC 是应用特定集成电路(Application-Specific Integrated Circuit)。
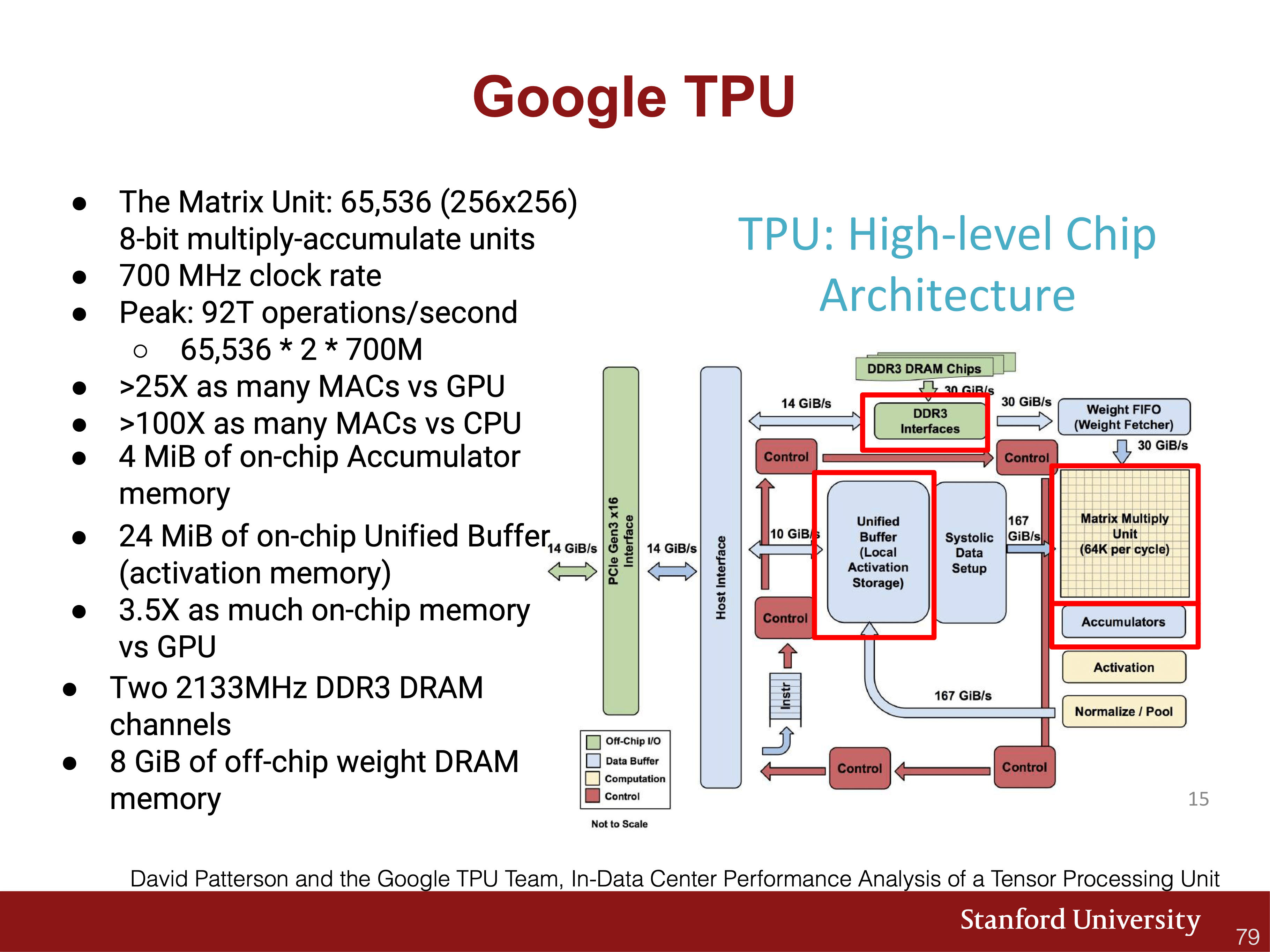
TPU就是一個ASIC。
核心是一個 MMU (Matrix Multiply Unit),這個芯片可以做到每個 clock circle 運算 65536 次矩陣乘或加。乘 700 MHz ,throughput 就高達每秒 92 T 次矩陣乘操作。
Algorithms for Efficient Training
- Parallelization
- Mixed Precision with FP16 and FP32
- Model Distillation
- DSD: Dense-Sparse-Dense Training
Parallelization
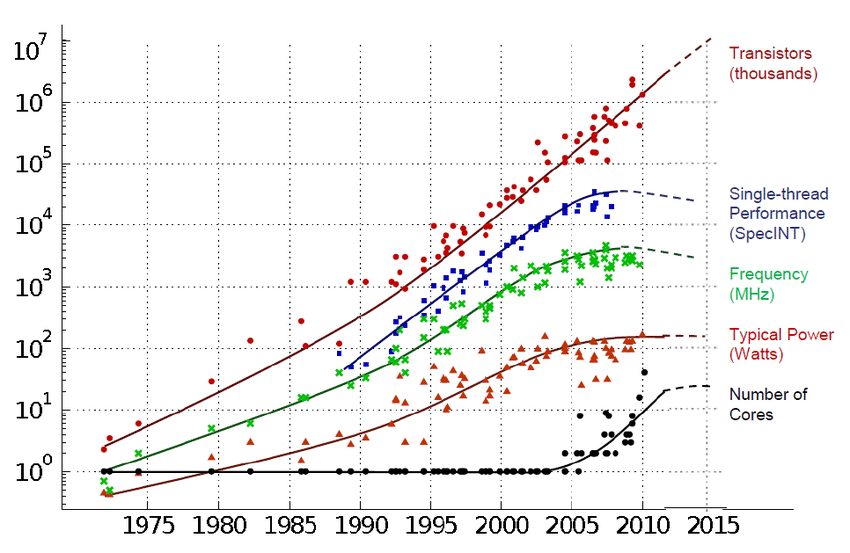
單核性能已經到頂了,因為 1. 晶體管已經很難再縮小幾納米,就決定了clock circle很難再縮短;2. 再提高頻率會增大功耗導致過熱和電源問題。
所以要尋求並行化。
Data Parallel,即分布式計算的做法,用一個 master server 和一堆 slave servers 用分布的數據計算前向後向;

Model Parallel,類似 LSTM 計算門的做法,把 weight 矩陣切開在多個 core 上計算。

Mixed Precision with FP16 and FP32
FP: Floating Point
混合精度訓練只有在更新梯度的時候用 FP32,因為累加會有精度累积,如果用 FP16 會損失更多精度,乘法無所謂。
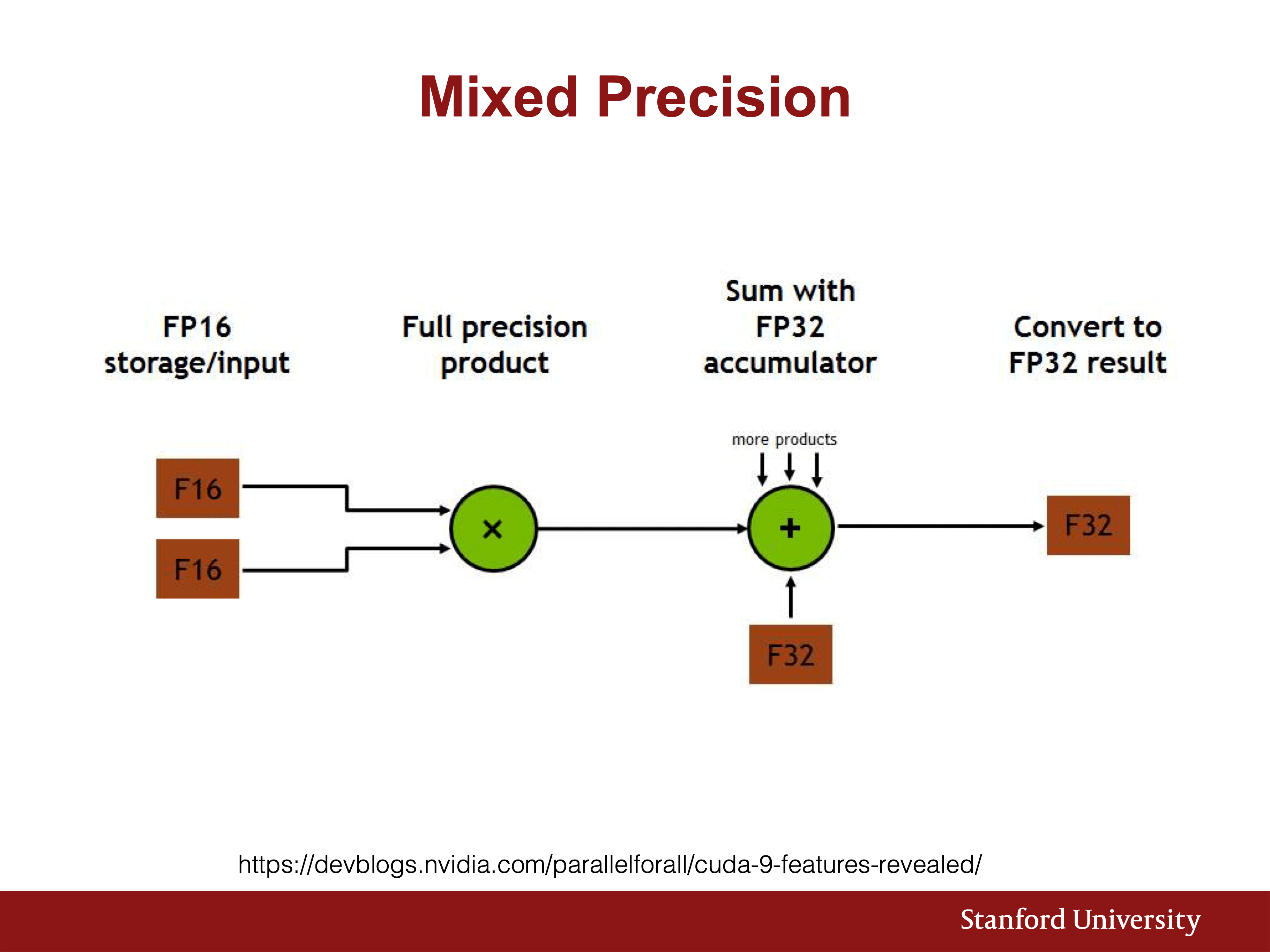 |
 |
Model Distillation
用教師模型 ensemble 即加權平均的 outputs 作為學生模型的 labels,即所謂軟標籤(Soft Targets),学生模型不仅学习从标注数据中获得的“硬标签”(例如“猫”),还学习教师模型提供的“软标签”。软标签提供了更多的细节信息,例如哪些类别可能较为相似,这有助于学生模型更好地学习复杂的决策边界。
學生模型的 y 就是教師模型的預測概率分佈,隱含了類別間的相對關係。
損失函數用 KL散度,衡量學生和教師模型的預測分布的差異。
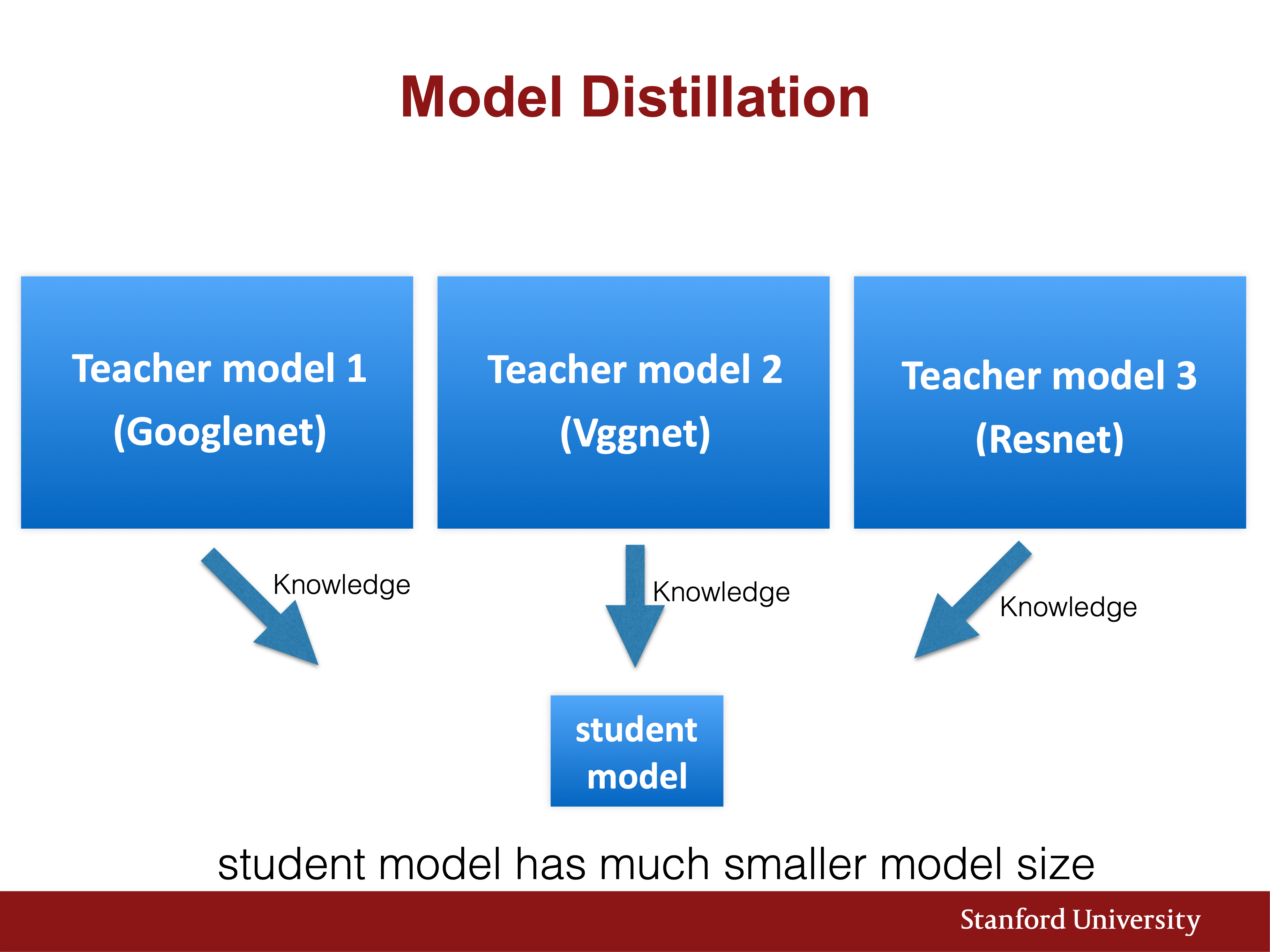
Hardware for Efficient Training
computation和memory bandwidth是兩個bottleneck,每個GPU/TPU/EIE都是要看這倆參數。
專門面向deep learning的Volta GV100 (2017),有tensor flops/tensor core。
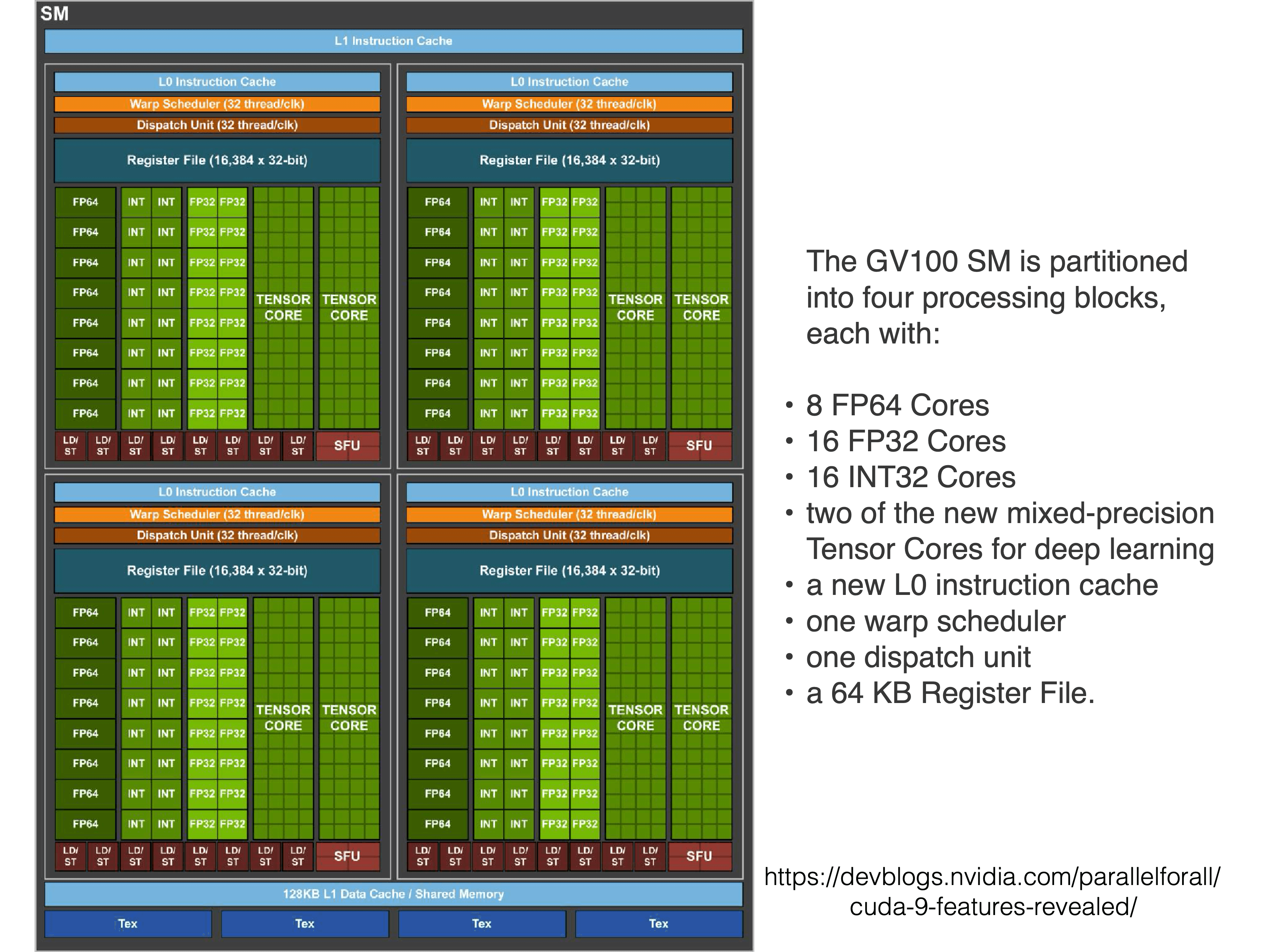
| Tesla Product | Tesla K40 | Tesla M40 | Tesla P100 | Tesla V100 |
|---|---|---|---|---|
| GPU | GK110 (Kepler) | GM200 (Maxwell) | GP100 (Pascal) | GV100 (Volta) |
| GPU Boost Clock | 810/875 MHz | 1114 MHz | 1480 MHz | 1455 MHz |
| Peak FP32 TFLOP/s | 5.04 | 6.8 | 10.6 | 15 |
| Peak Tensor Core TFLOP/s | - | - | - | 120 |
| Memory Interface | 384-bit GDDR5 | 384-bit GDDR5 | 4096-bit HBM2 | 4096-bit HBM2 |
| Memory Size | Up to 12 GB | Up to 24 GB | 16 GB | 16 GB |
| TDP | 235 Watts | 250 Watts | 300 Watts | 300 Watts |
| Transistors | 7.1 billion | 8 billion | 15.3 billion | 21.1 billion |
| GPU Die Size | 551 mm² | 601 mm² | 610 mm² | 815 mm² |
| Manufacturing Process | 28 nm | 28 nm | 16 nm FinFET+ | 12 nm FFN |
Lecture 16
- What are adversarial examples?
- Why do they happen?
- How can they be used to compromise machine learning systems?
- What are the defenses?
- How to use adversarial examples to improve machine learning, even when there is no adversary
What are adversarial examples?
You’re probably used to following the gradient on the parameters of a model.
You can use the back propagation algorithm to compute the gradient on the input image using exactly the same procedure that you would use to compute the gradient on the parameters.

Ian第一次实现时不敢相信是正确的代码,以为是bug,所以特地把输入和输出拿出来用numpy算difference。
這裡的做法是之前Lecture 12裡講的用錯誤類別對input image做gradient ascent,可以做到fool spam欺騙模型,人眼看還是兩個大熊貓,模型區分不了,而模型能區分人眼區分不了的 Alaska Husky 和 Siberian Husky。

Why do they happen?
but then because this is a very complicated function and it has just way more parameters than it actually needs to represent the training task, it throws little blobs of probability mass around the rest of space randomly.
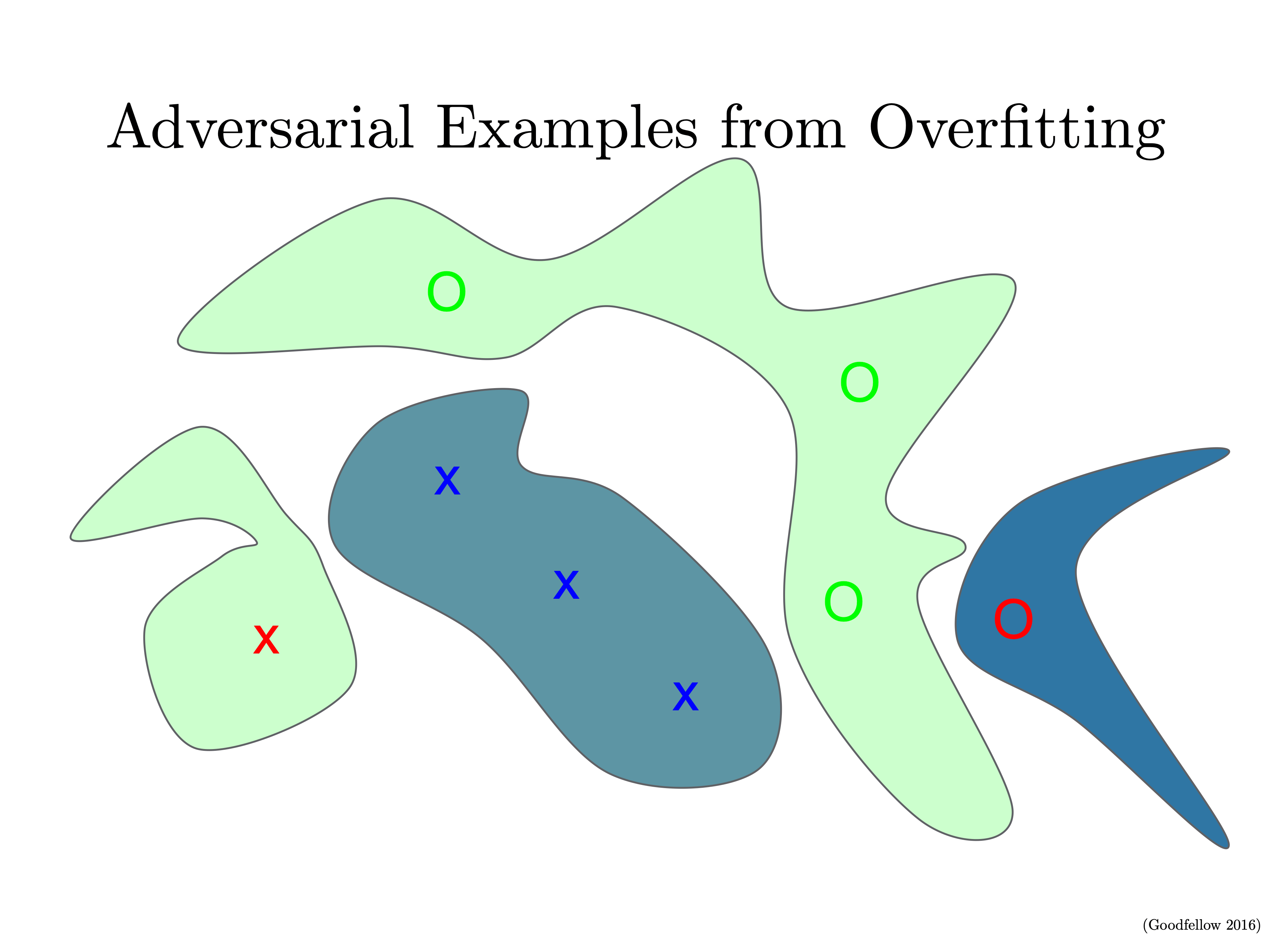
他們首先認為這是overfitting導致的,但是如果真的是過擬合導致的,那按理說這個 model 是個 unique bad luck,如果重新 fit 一遍或者 fit 個略微不同的模型,應該會出現其他 random different adversarial examples,
但是事實是很多不同的模型都會 misclassify the same adversarial examples,甚至是分到同樣的類裡,而且發現 adversarial example 減 original example,得到的 offset vector 有相同的方向,把這個加到任何 clean example 上都會得到 adversarial example。
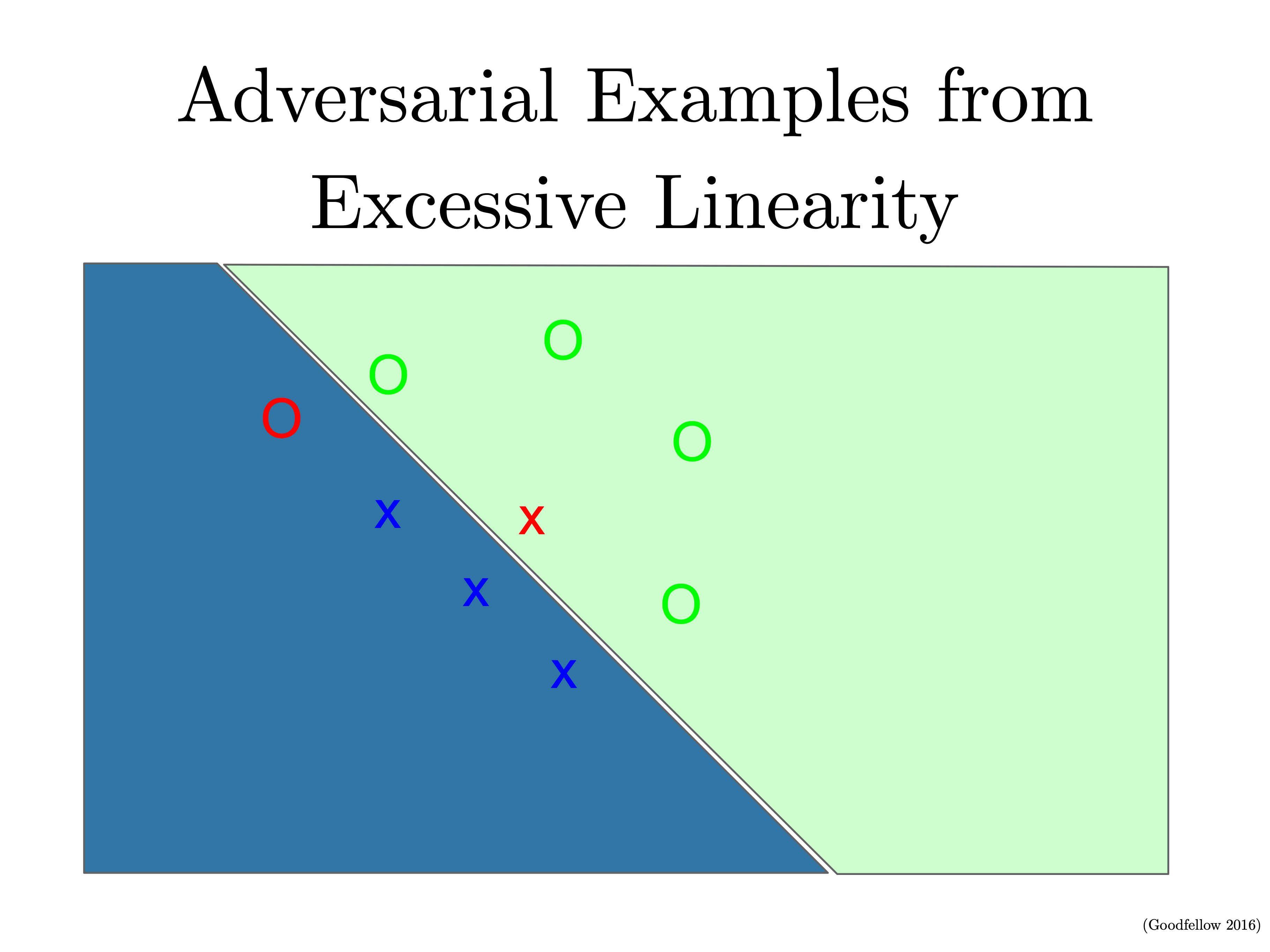
所以或許是欠擬合導致的。
Modern deep nets are very piecewise linear
一個很神奇的思路:input和output是piecewise linear function的關係。。但是每層的weights matrices是乘在一起的所以是非常non-linear的,這部分導致訓練很難,好像確實是,input並沒有乘自己所以是一次關係
But the mapping from the input to the output is much more linear and predictable, and it means that optimization problems that aim to optimize the input to the model are much easier than optimization problems that aim to optimize the parameters.
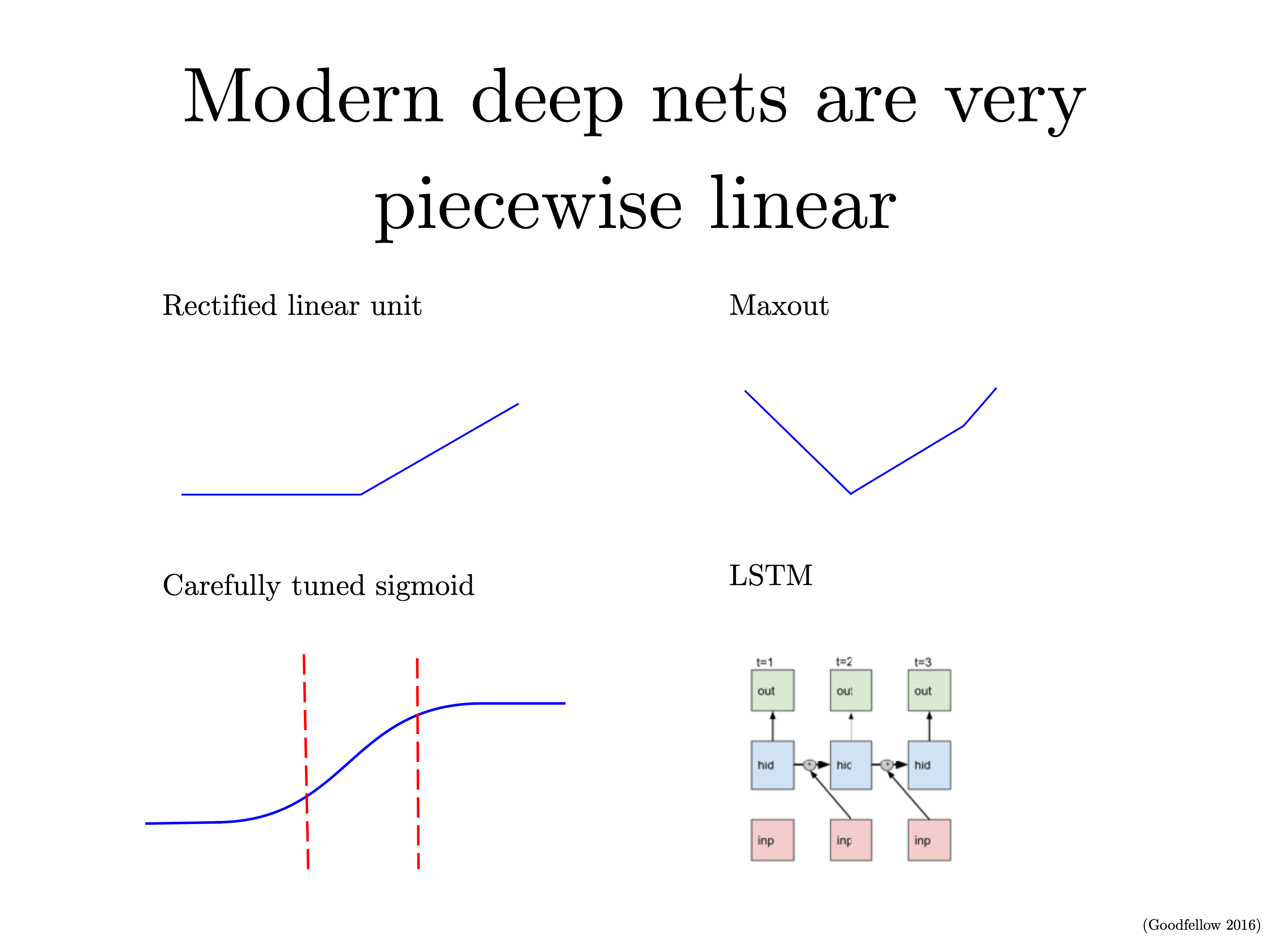
本來WX就是線性的,這裡展示的 non-linearity有效區間也幾乎都是線性的。
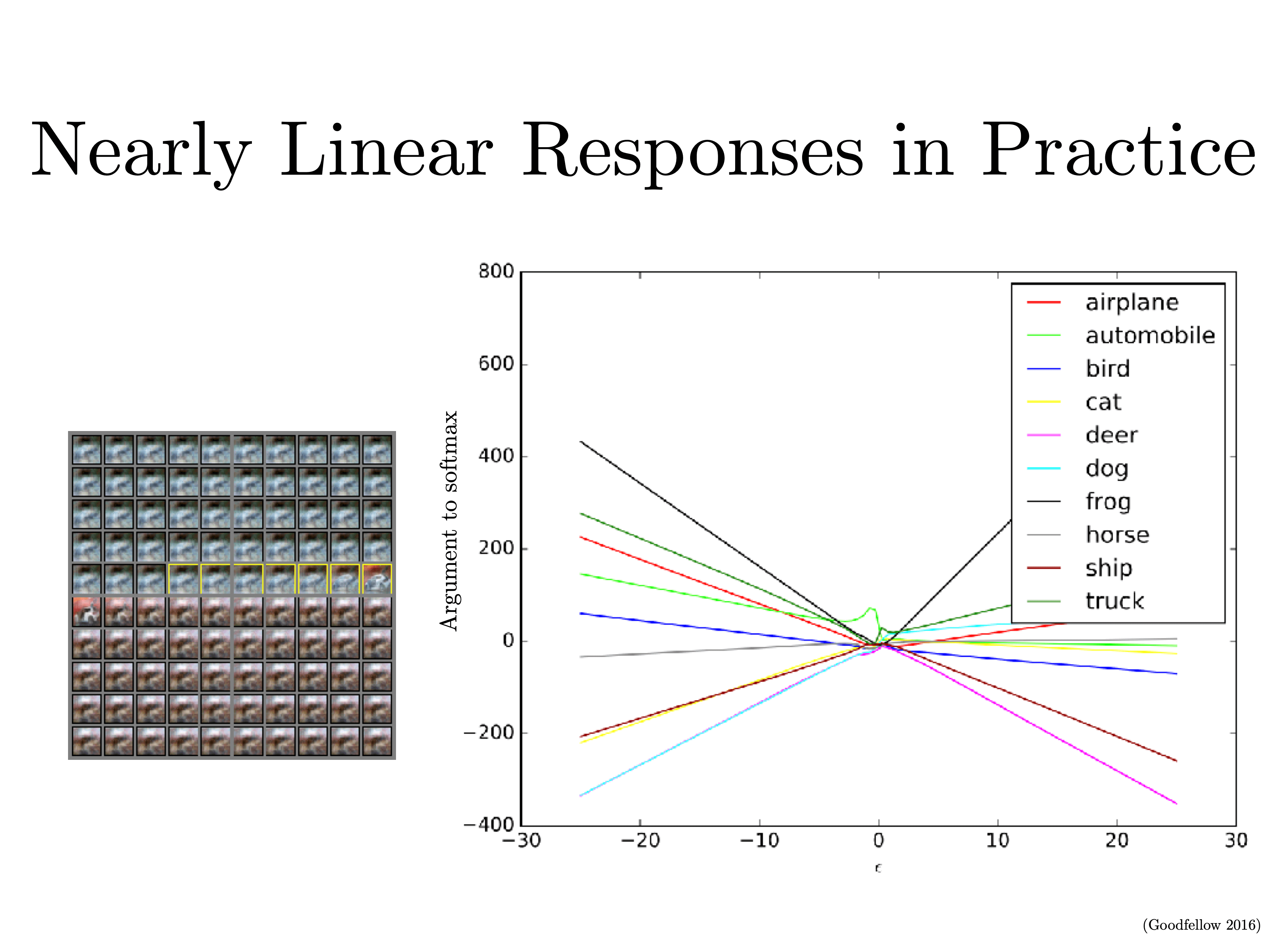
Nearly Linear Response 這個slide裡,實驗是選了一個白車紅底圖,選了一個這張圖將travel through space的方向,然後 $\epsilon$ 乘這個方向,加在input image上, $\epsilon = 0$ 就是原圖。
左邊的是 $\epsilon$ 從 -30 到 +30 的animation,黃框的是分類正確的。
右邊的是這個 deep convolutional rectified linear unit model (CNN with ReLU) 輸出的 logits。
可以看到 car 在這裡是 automobile, $\epsilon = 0$ 時logits最大。而改變 $\epsilon$ 時變化最大的是 plot 裡的 brown curve,frog 類,正確的 automobile 分類在這個方向上移動時遠不如 frog 變得快。
所以這個方向也許就是跟蛙類相關的方向。
就像“Adversarial Examples from Excessive Linearity” 認為不是過擬合反而是欠擬合時,說的那樣的位置/方向,linear model 有很高的 confidence 給角落裡沒見過樣本的位置。
Adversarial examples存在就是因為模型非常線性,上面CNN的曲線也印證了這一點,logits對input線性變化的反應也是線性的。

Small inter-class distances 這裡也說明,即使用一個比平常用的 reg 7 小的 L2 norm 3.96,也可能造成肉眼上非常大的變化,所以其實人眼不可見的變化也許是會讓 input go really far 並且乘 coefficient W 的時候在這個方向上變得很大。
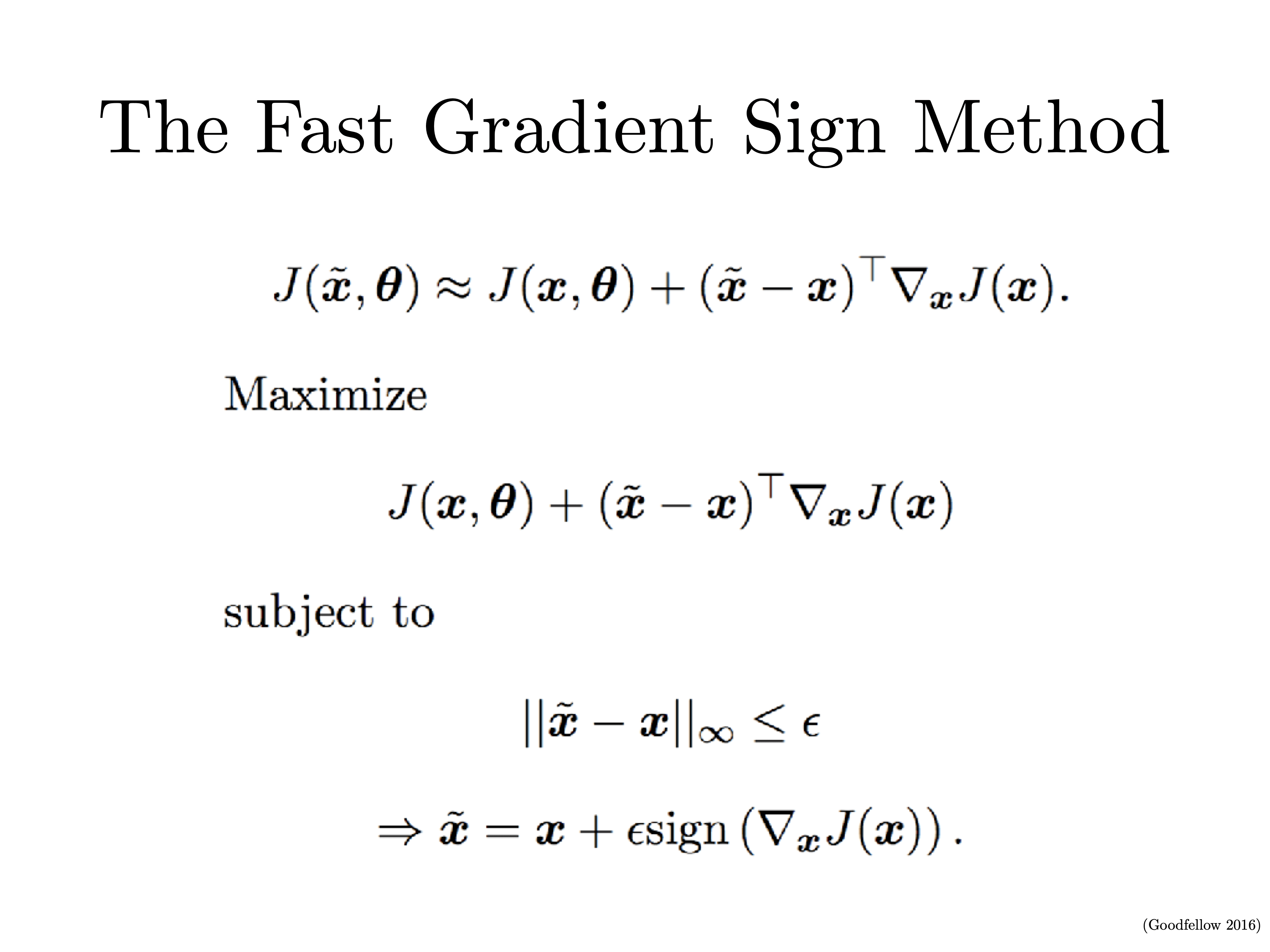
The Fast Gradient Sign Method 就基於這種 neural nets 其實非常 linear 的觀察,認為梯度方向就是一個生成上面所說的這種 adversarial example 最快的方向,根據 Taylor series approximation 泰勒展開得到上面的公式,基於此推導出底下更新出 adversarial example 的公式。
Ian說人們很難找到真的好過fast gradient sign(gradient ascent這樣)的構造方式,Nicholas Carlini’s attack 也值得嘗試。The Fast Gradient Sign Method 攻擊沒有 special defenses 的 regular neural nets 有 99% 的成功率。
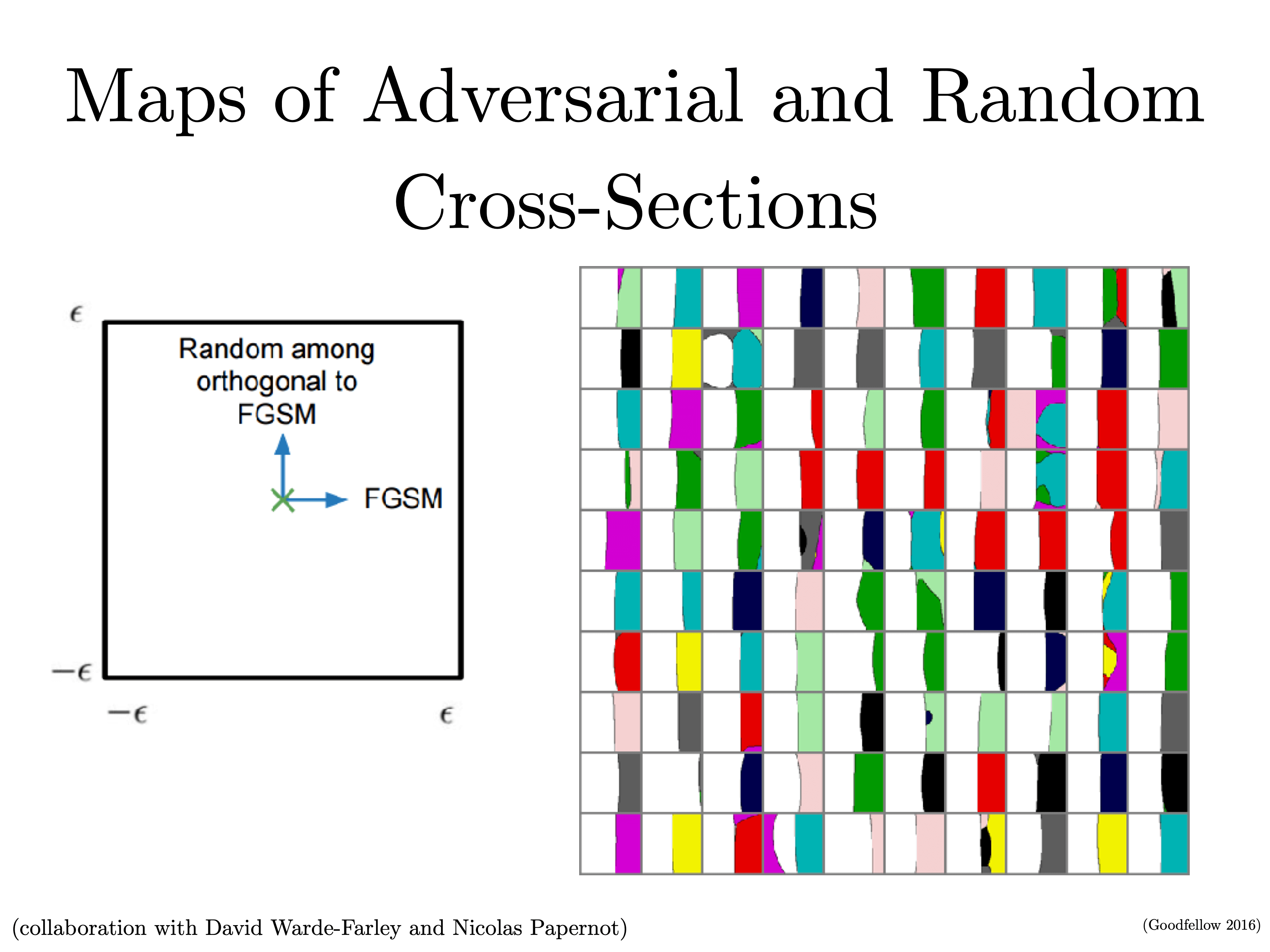
Maps of Adversarial and Random Cross-Sections 他們做的這個“橫截面” decision boundary 圖是另一個 evidence。FGSM 就是上面這個簡稱。
每個cell對應一個 CIFAR-10 的樣本,白色的是正確分類,彩色是其他錯誤分類,x axis 方向是樣本沿 FGSM 的梯度方向改變,y axis 方向是 orthogonal 梯度正交的方向。
可以看到 adversarial examples 的區分是個 linear subspace,不像上面的圖裡假設的那樣 adversarial examples 只是一堆個例 blob,因此只要用一個跟 gradient 點積較大的方向就可以構造 adversarial examples 了。
最後還有個加噪聲方向的對比圖,用隨機噪聲其實會讓模型要麼完全分類錯,要麼完全分類對。這是因為在高維空間裡,隨機向量幾乎一定和選定的參考向量(random noise的方向)正交。
在高維度裡為什麼隨機找一個random vector跟reference vector很可能是正交的?有點反直覺?
Reference vector(参考向量)是一个在某个空间或上下文中用于描述或标定其他向量的基准向量。具体来说,参考向量通常用于对比、计算、映射或表示其他向量的方向、大小等特征。
在高维空间中,参考向量的定义可以根据问题的背景有所不同。比如在一些机器学习或信号处理中,参考向量可以用来表示某种特征,或者作为某种算法的“标准”,其他的向量可以相对于参考向量进行比较。
为什么随机选择一个向量与参考向量正交的可能性很高?
这个问题的反直觉性主要来源于高维空间中的几何性质。具体来说,高维空间中的向量之间的相互关系与我们在低维空间(如二维或三维空间)中的直观理解非常不同。在高维空间中,随机选择的向量与某个固定向量(如参考向量)正交的概率实际上是非常高的,原因可以从以下几个方面理解:
1. 高维空间的几何特性:
在二维或三维空间中,随机选择的向量与某个固定向量正交的概率是零,因为正交的向量只可能在一个特定的方向上(例如,在二维空间中,只有与参考向量垂直的那条直线上的向量才会正交)。然而,在高维空间中,正交向量的集合(即与参考向量垂直的所有向量)所形成的子空间的维度远大于低维空间。
- 在高维空间中,给定一个参考向量,它所确定的“正交子空间”的维度非常高。假设我们在 $n$-维空间中,参考向量 $\mathbf{v}$ 所确定的正交子空间是一个 $n-1$ 维的子空间。
- 任何一个随机选择的向量,如果它位于这个 $n-1$ 维的正交子空间中,那么它就会与参考向量正交。
2. 随机向量的分布:
在高维空间中,随机选择的向量往往“几乎”是正交的。随机选择的向量可以看作是从一个单位球体(即所有向量的长度为1的集合)中随机选择的。如果我们取一个随机向量,它与参考向量的夹角大多数情况下会非常接近90度(即正交),这是因为高维空间中的向量几乎是均匀分布的,且任何两个向量之间的夹角都有很大的可能性接近于 $90^\circ$。
3. 高维空间中的内积接近于零:
在高维空间中,内积的期望值趋近于零。如果你随机选择一个 $n$-维向量,并且将它与一个固定的参考向量做内积,由于高维空间的“稀疏性”,这个内积值通常接近零,这意味着随机向量和参考向量几乎是正交的。
4. 高维空间的“球面集中性”:
随机向量在高维空间中的分布有一个有趣的现象,称为球面集中性。随着维度的增加,大多数随机向量的方向都趋于均匀分布。对于一个随机选择的向量,它与任何固定参考向量的夹角都会趋向于均匀分布,且大部分时间夹角都接近于90度,这使得它们在高维空间中呈现“正交”的特性。
直观的理解:
- 在二维或三维空间中,两个向量要正交,它们必须满足某种特定的几何关系(90度或說垂直),因此它们在几何上是“特殊”的。
- 然而,在高维空间中,大多数向量之间的关系都趋向于“随机”。当你随机选择一个向量时,几乎可以认为它在一个高维的“球面”上,它与参考向量几乎是随机的,且有非常高的概率接近正交。
数学上的说明:
- 假设参考向量是 $\mathbf{v}$,随机向量是 $\mathbf{r}$,它们的内积 $\mathbf{v} \cdot \mathbf{r}$ 表示它们之间的相似度。随着空间维度的增大,内积的期望值趋近于零,因为大多数向量几乎处于与参考向量正交的状态。
总结:
在低维空间中,我们直观地认为两个向量之间的关系是比较特殊的(例如正交),但在高维空间中,随机选择的向量与参考向量正交的概率非常高,这是由于高维空间中正交子空间的维度很大,以及高维空间中向量之间的内积趋向于零,导致随机向量与参考向量几乎是正交的现象。
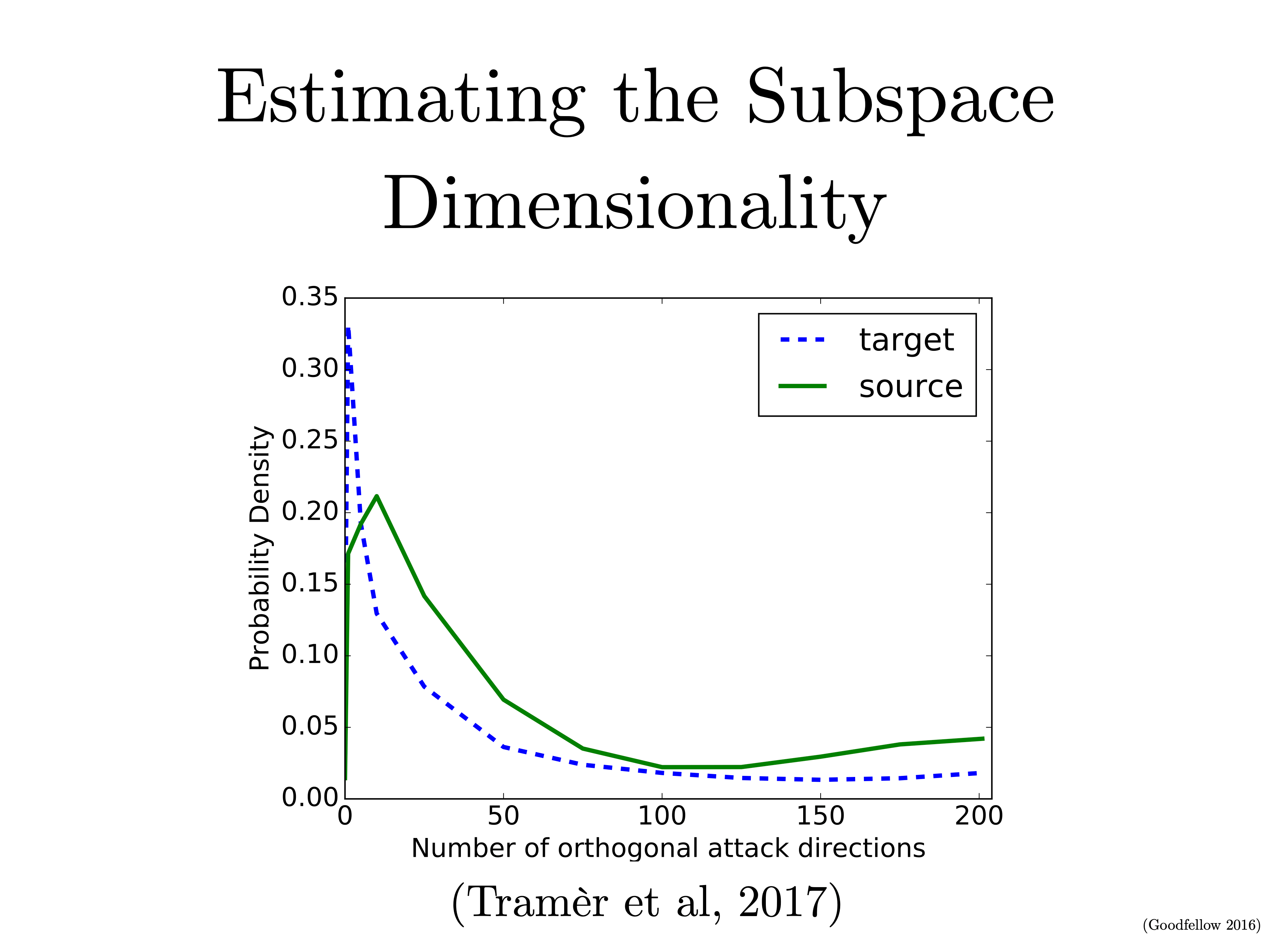
這個Stanford的工作是在MNIST(28 x 28 = 784 維,手寫數字單通道)上做的,有25個跟 gradient 點積大的方向,也就是說一個 attacker 有 10% 的機率隨機用噪聲騙過模型。
很像 Clever Hans 這匹誤以為會 arithmetic 的馬,model 學到的 “linear” function 只會在跟 training set 分布類似的 test set上有好效果,如果 shift a little 比如在這 25 個 adversarial direction 上變化就沒有泛化能力了。
adversarial FGSM 也可以讓很難失敗的 RL 算法失敗。
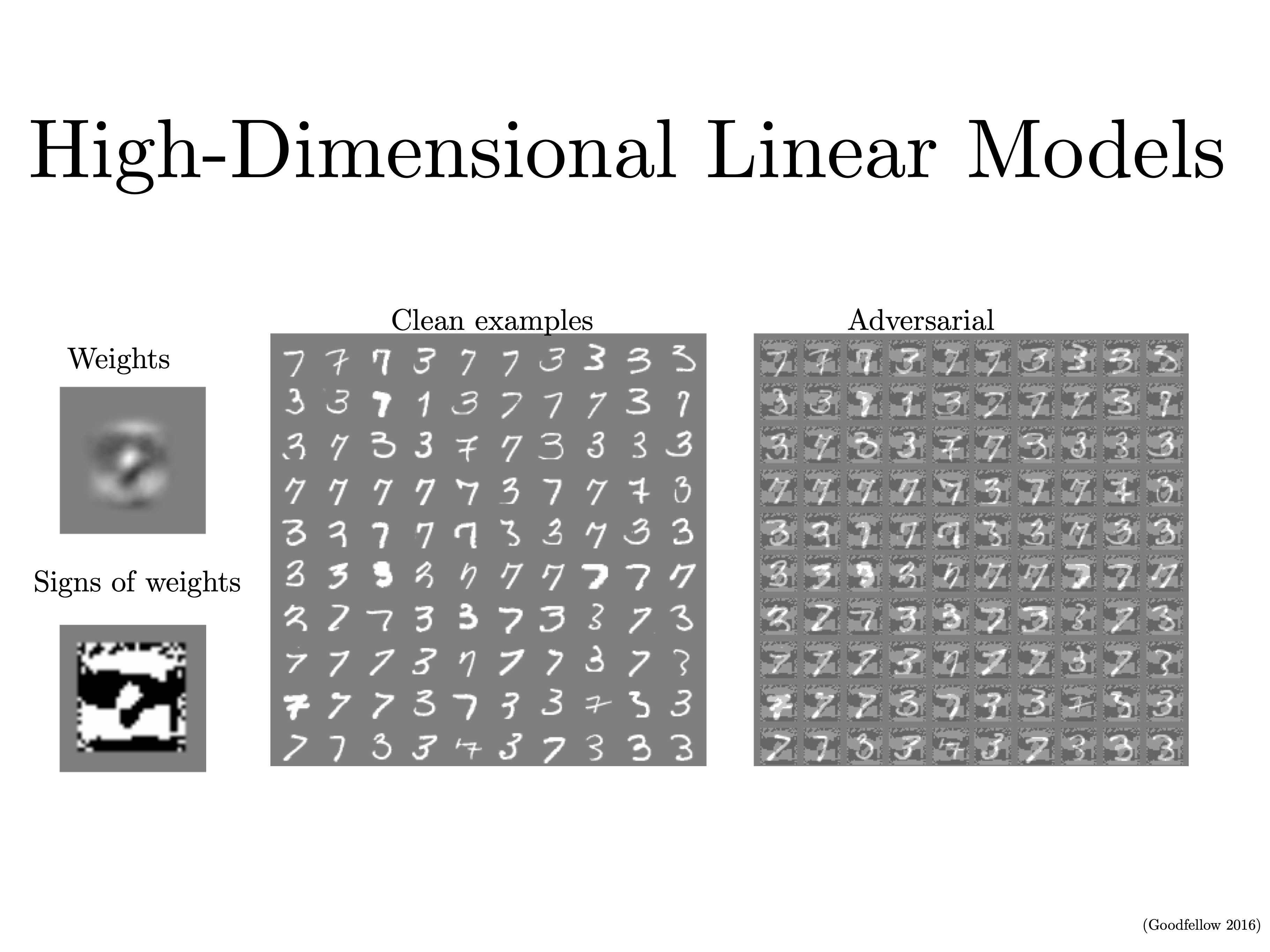
這個分辨 7 和 3 的任務裡,weights 應該長得像它倆的區別(因為會同時學習 7 和 3 的關鍵特徵,這也正是它倆的區別)。
他當時發現 RBEs behave more intuitively,但是回傳梯度總是變0,他沒能訓練成功很深的RBF,如果有人有更好的優化方法也許能解決adversarial問題,不知現在如何。
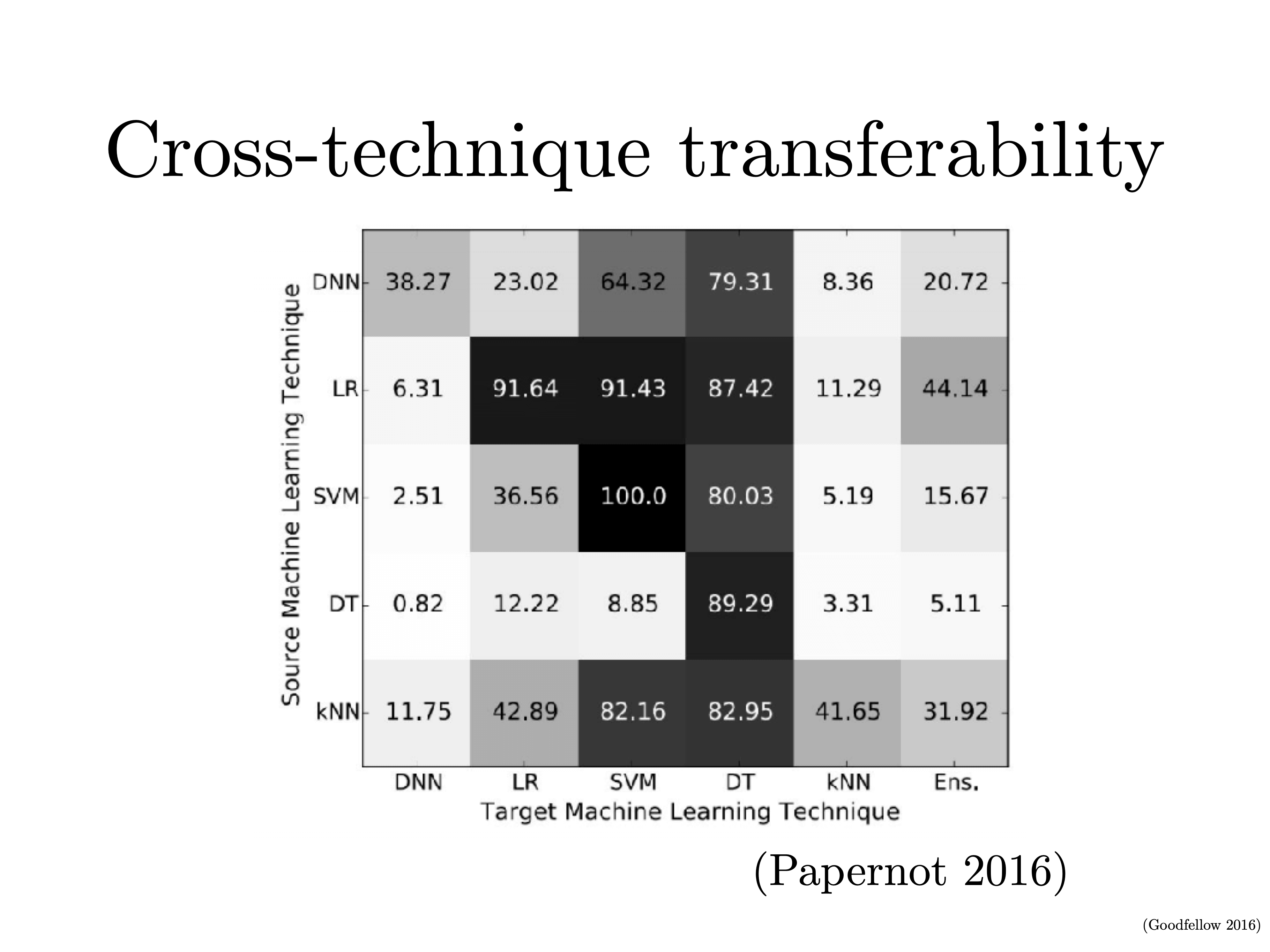
不同的模型能轉化!
- attacker 可以在目標任務數據集上訓一個模型找 adversarial examples 騙過目標模型。
- 目標任務數據集獲得不到,但是能訪問目標網絡的話,可以給它一些輸入,得到一些結果,然後用這來訓練自己的模型。

這個圖裡 ensemble 了除了每行第一個外的其他四個模型,后面被 ensemble 的模型不可能分類正確,沒被 ensemble 的模型正確率也很低。
甚至有個 malGAN 繞過 malware detectors 恶意软件(Malicious Software)。
What are the defenses?

Ian 說就算你讓模型訓練應對了一種defense,但因為是 non stationary 的,它會對另一種 attack 變得 vulnerable。
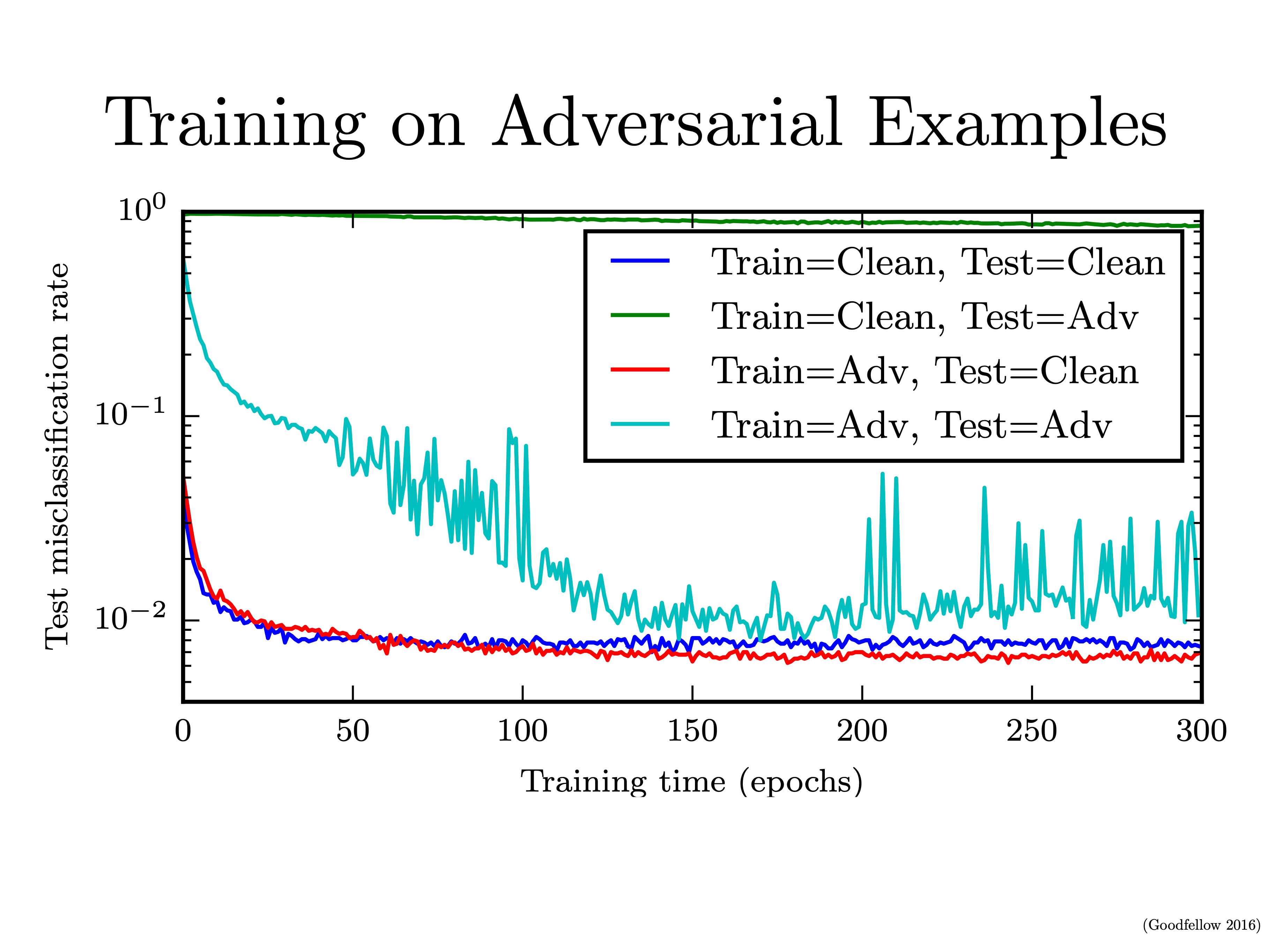
我一直想問的問題,如果訓練的時候加入攻擊樣本呢?——Training on Adversarial Examples
adversarial training 是 data hungry 的,每次更新參數都要生成新的數據,也很合理,畢竟每次更新參數時才能拿到 dLoss over dX。
QA階段:他的思路是,如果一個現象出現次數超過 80% 就會放進 slide 裡並試圖解釋它,比如上面的 weird things 比如上面的 frog class。
關於上面說的數據總維度和 adversarial 維度的關係(比如 MNIST 的實驗裡是 25 over 784 大約 3%),他也沒有具體概念,他只在兩個數據集上跑過,因為當時是在 OpenAI 離職和去 Google 之間的時間,所以只在筆記本的 CPU 上跑了這個代碼,沒有 GPU。
來讀研三年半只有商湯的半年真的感覺自己在做科研。
Stanford和Berkeley都專門有GAN的課,CS236和CS294-158。
Lecture 17 Attention and Transformers
2024的Lecture 8,或者2019的Lecture13。
seq2seq with vanilla rnn or lstm
回顧上面 Lecture 10 提到的多種 rnn 結構/任務的 computational graph 裡,其中 sequence to sequence 任務是 many to one + one to many 的形式,上面只是推理時的結構,這裡用seq2seq任務舉例,先細化訓練時的做法。
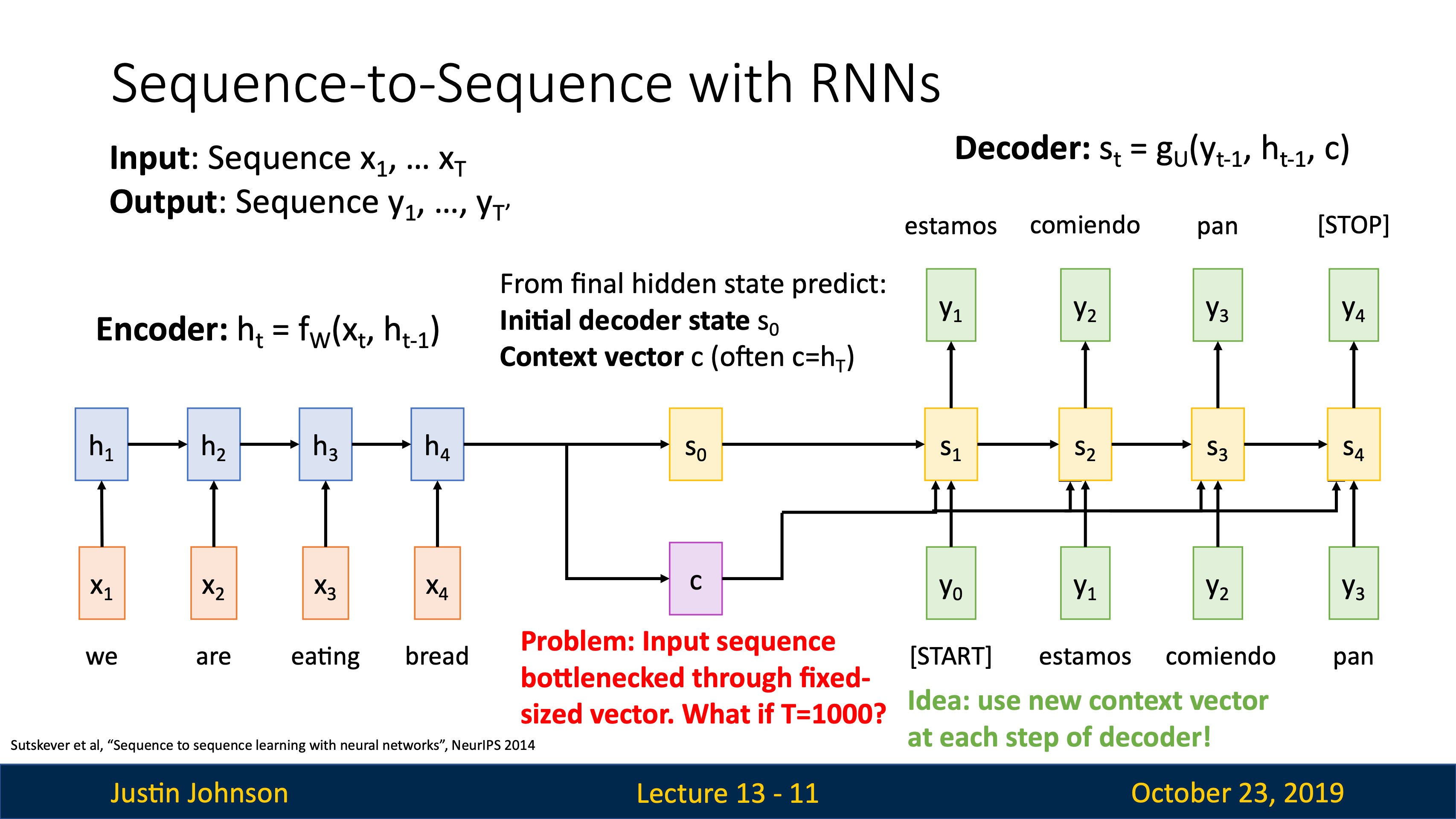
這裡的 context vector c 就是 $h_t$ 最後一個 hidden state,$s_0$ 就是類似 $h_0$ 或 $c_0$ 的初始化 decoder 裡的 hidden state。(這裡cs231n看圖的意思是s0不用ht初始化,JJ講的Michigan Online是說s0也要用ht初始化,见图)訓練時不一樣的是會給 decoder 每一個 time step 都輸入 ground truth token。
- 訓練時 teacher forcing:就算預測是錯的也會用 correct token 作為下個 time step 的輸入,強迫 decoder 用 ground truth 訓練;
- 推理時 Test-time 最多只給 decoder 一個
<START>,也是 sample 到<STOP>或者<END>為止。
但是像圖裡說的,這裡有個問題是如果 Encoder 的 time step 太長,比如翻譯任務輸入一個 1000 詞的文本,只用“ c ”無法很好地承載/傳遞所有的信息,這個 c 就是所謂的 Bottleneck 瓶頸。
vanilla 或 LSTM 無法處理長序列的問題在於 c 這個 context 向量不能承載所有上下文信息,一個解決方案是在解碼時直接使用輸入序列的原始信息。
Attention
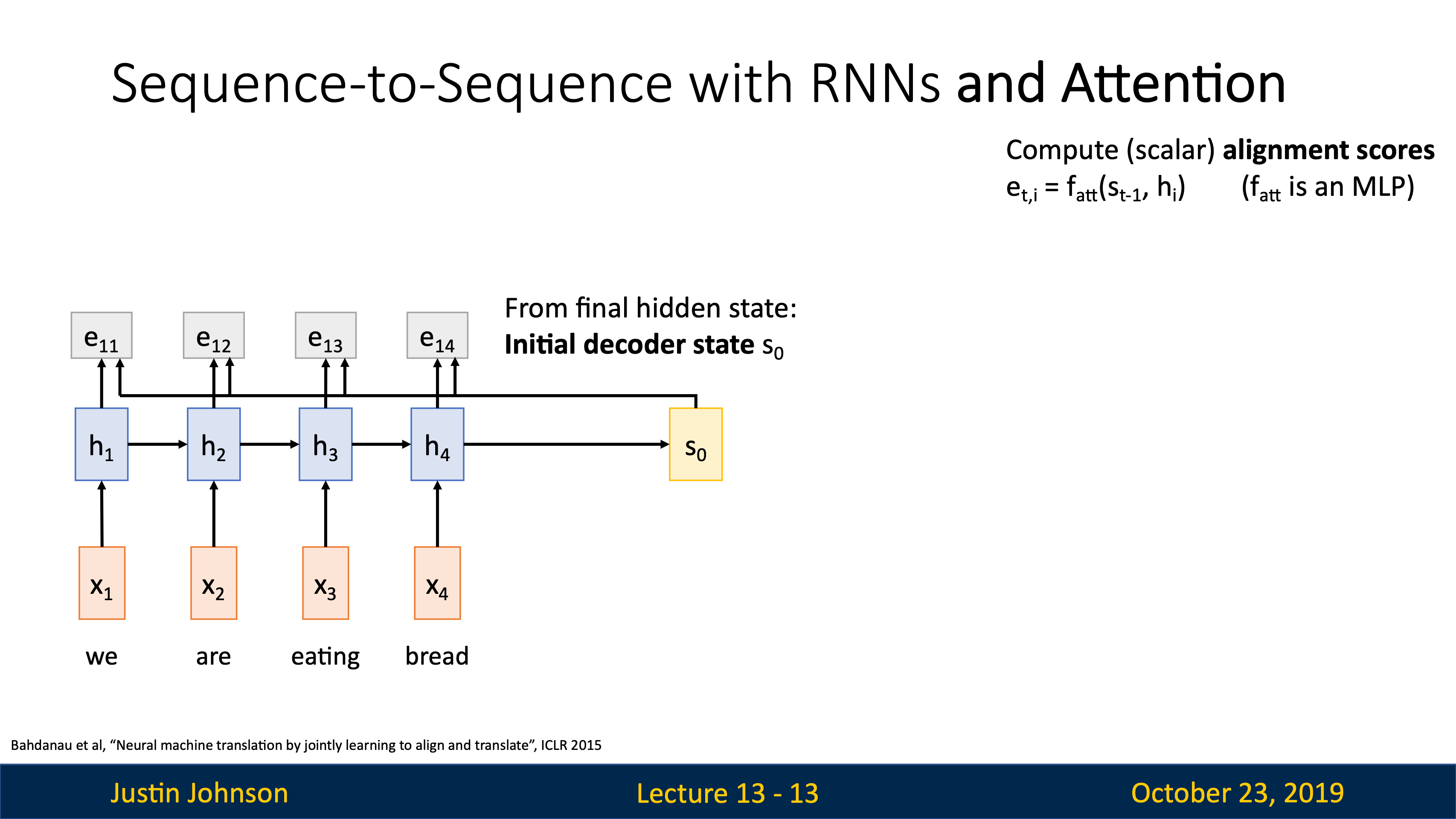
encoder還是一樣的,生成一個 $s_0$,但不直接輸入給 decoder 了,先用一個 alignment function(一個 FC) 把 Initial Decoder State $s_0$ 跟每一個 Encoder 的 Hidden State $h_{1/2/3/4…}$ 結合起來。
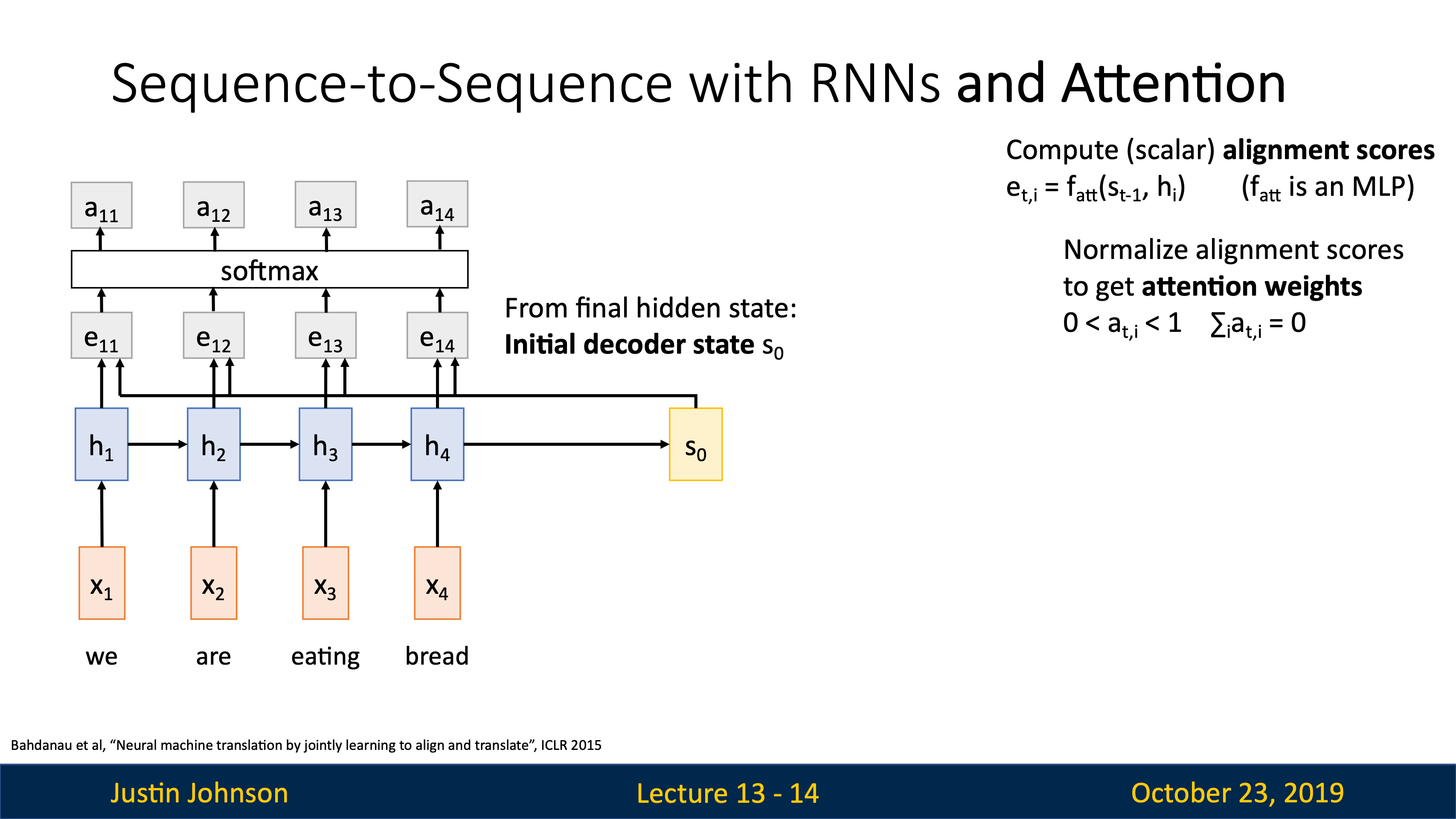
這個 Alignment Scores 的 Intuition 是:告訴我們在生成當前 Decoder 的 Hidden State $s_{1/2/3/4…}$時,Decoder 更希望關注哪些輸入。這個其實已經足夠了,但因為都是些 arbitrary real number,所以用 Softmax 整理成概率分佈,這個概率分佈就叫 Attention Weigths。
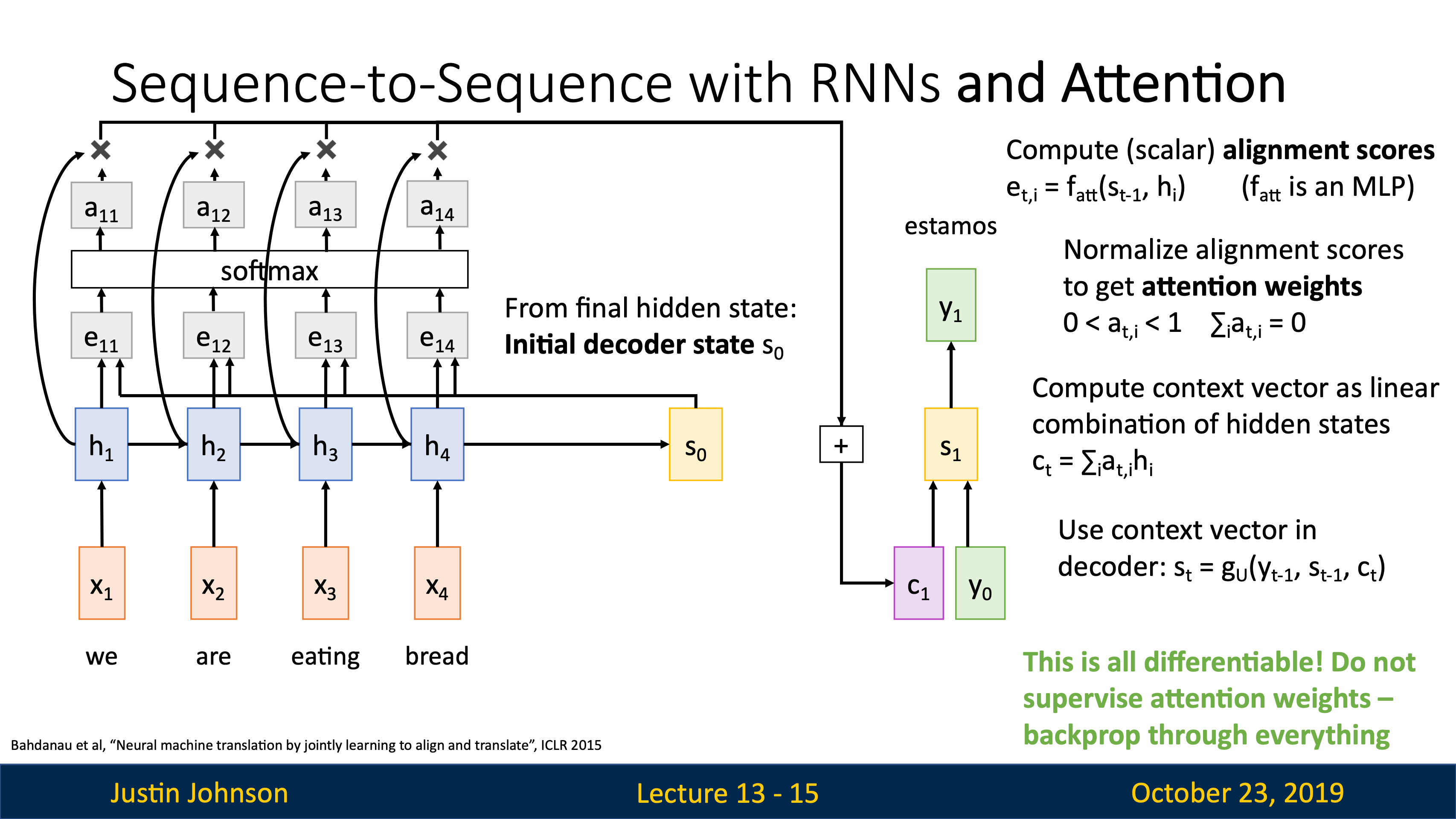
有了“Attention Weights”之後,像上面說的,我們希望的是“在解碼時直接使用輸入序列的原始信息”解決 Context Vector 承載能力太低的問題,所以就用 Weigths 跟每個 Time Step / 輸入 的 Hidden State 求 加權和 作為 Decoder 新的 Context Vector $c_{1/2/3/4…}$。
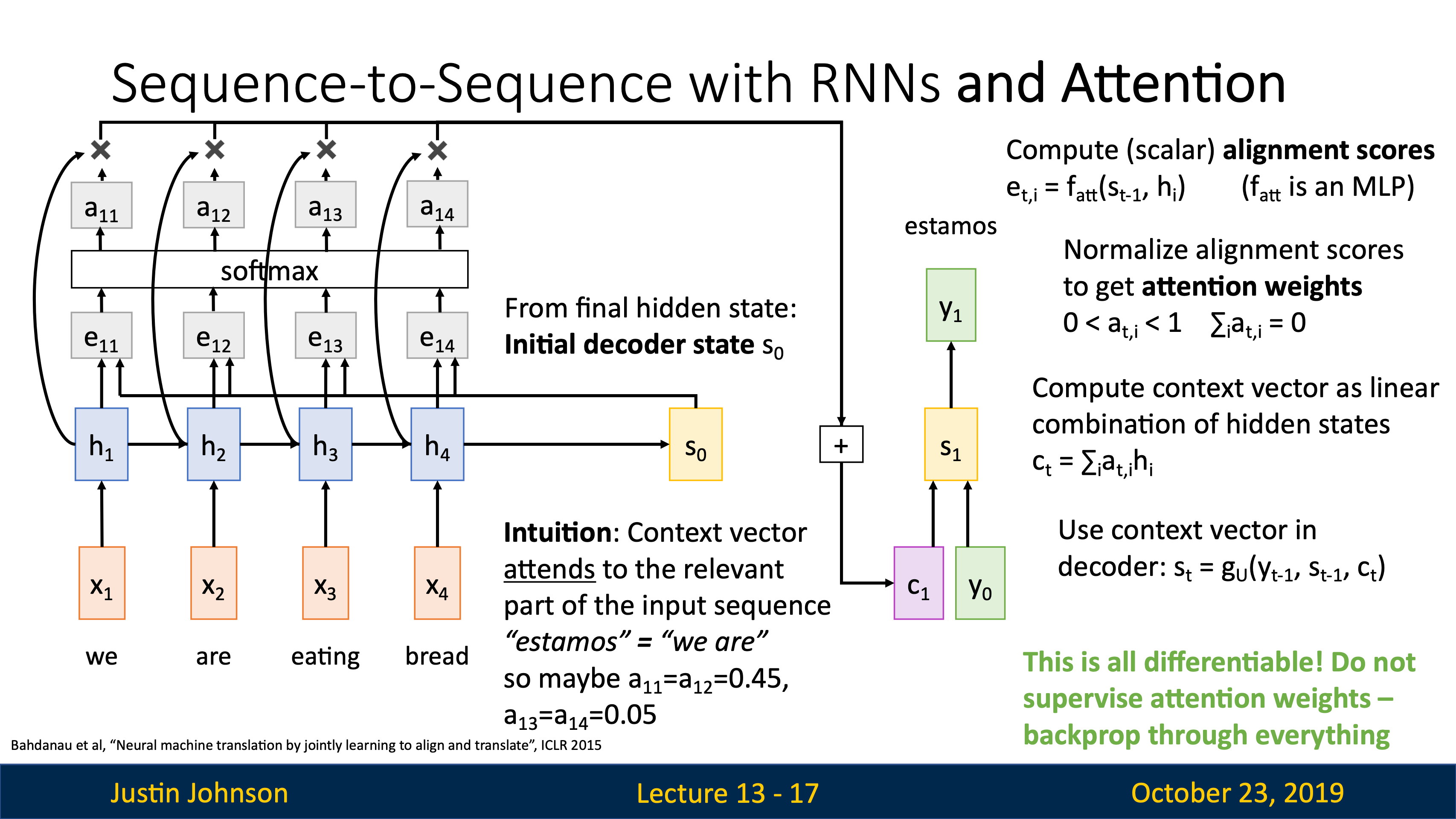
以機器翻譯為例,這樣做的直觀解釋是,比如要翻譯“我們是”為“we are”,decoder在預測 “we” “are” 時只需要關注 input sequence 裡的 “我”和“們”,而且這些不是提前設定的,是可導的、模型自己學到的,模型自己通過 jointly optimize 決定它更想關注哪部分。
| 一樣地,decoder 的第二個 time step 就用剛生成的 $s_1$ 計算新的 $e_{2x}, a_{2x}$ 和 weighted sum 即 context vector $c_2$ | 這時進行下一個 forward pass,用 c2 和剛預測的 $y_1$ 生成新的 hidden state $s_2$和$y_2$ |
|---|---|
 |
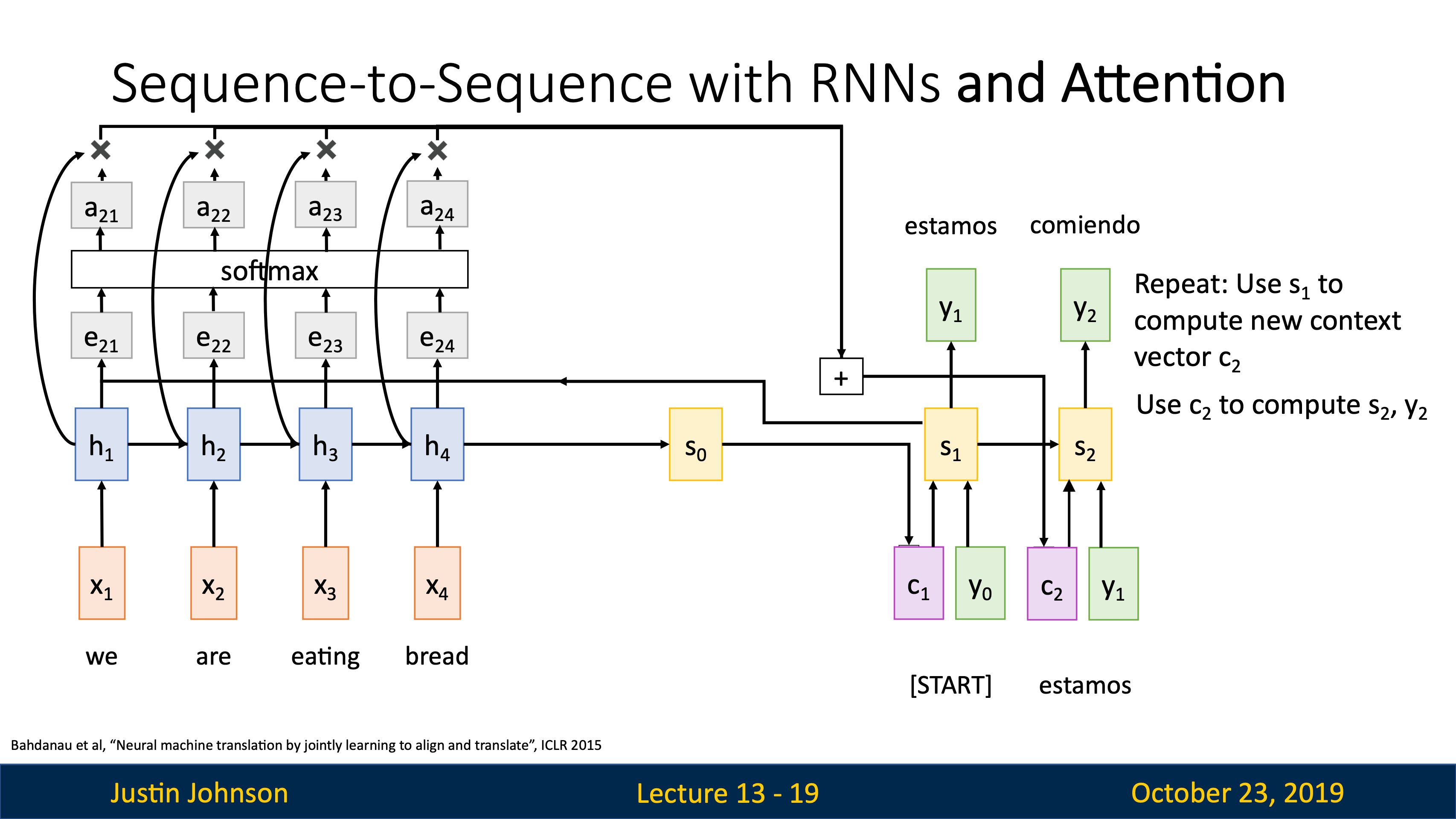 |
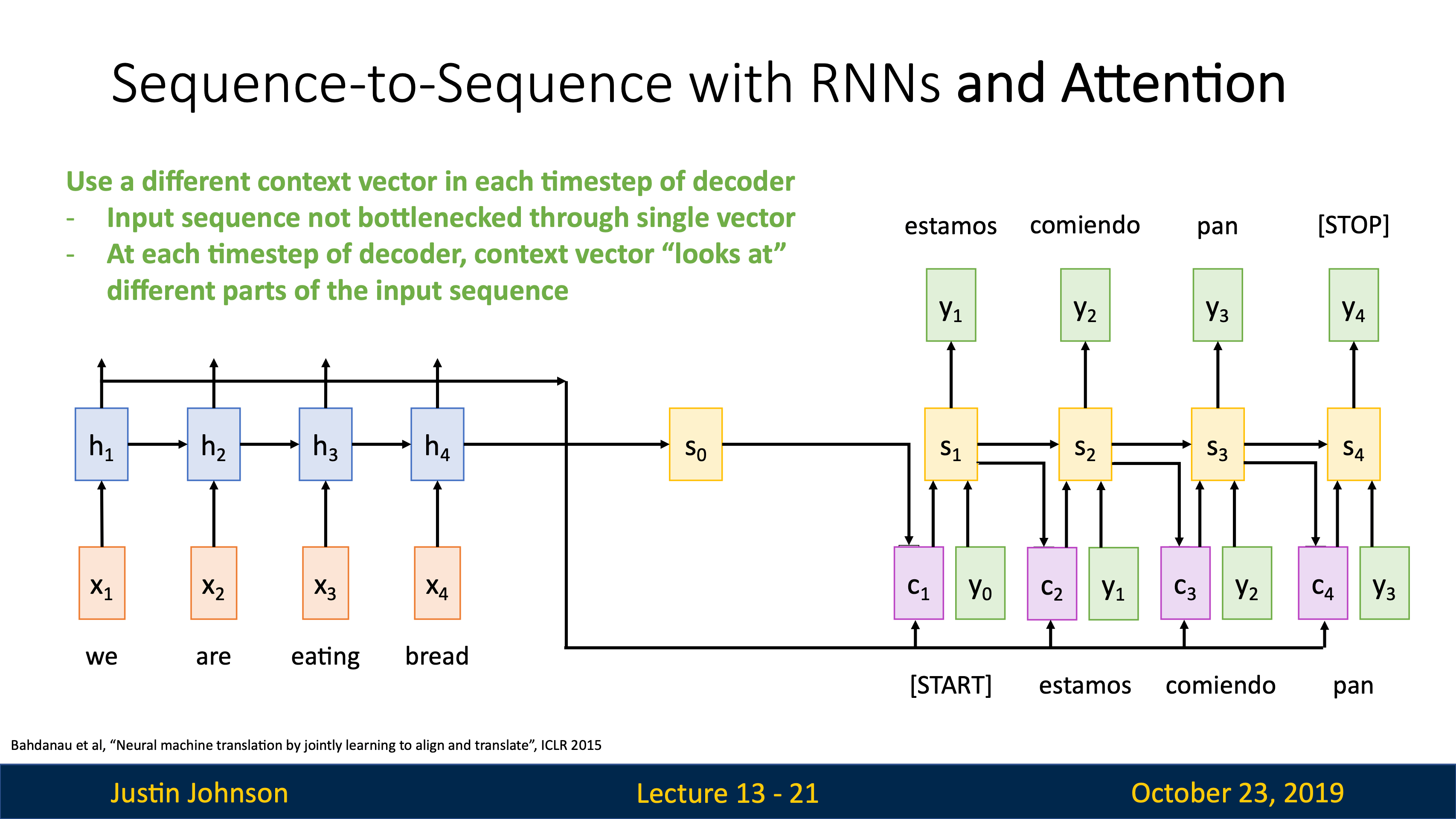
這樣就得到了用 Attention 解決 Context Vector 的 Bottlenecking 的新 RNN。
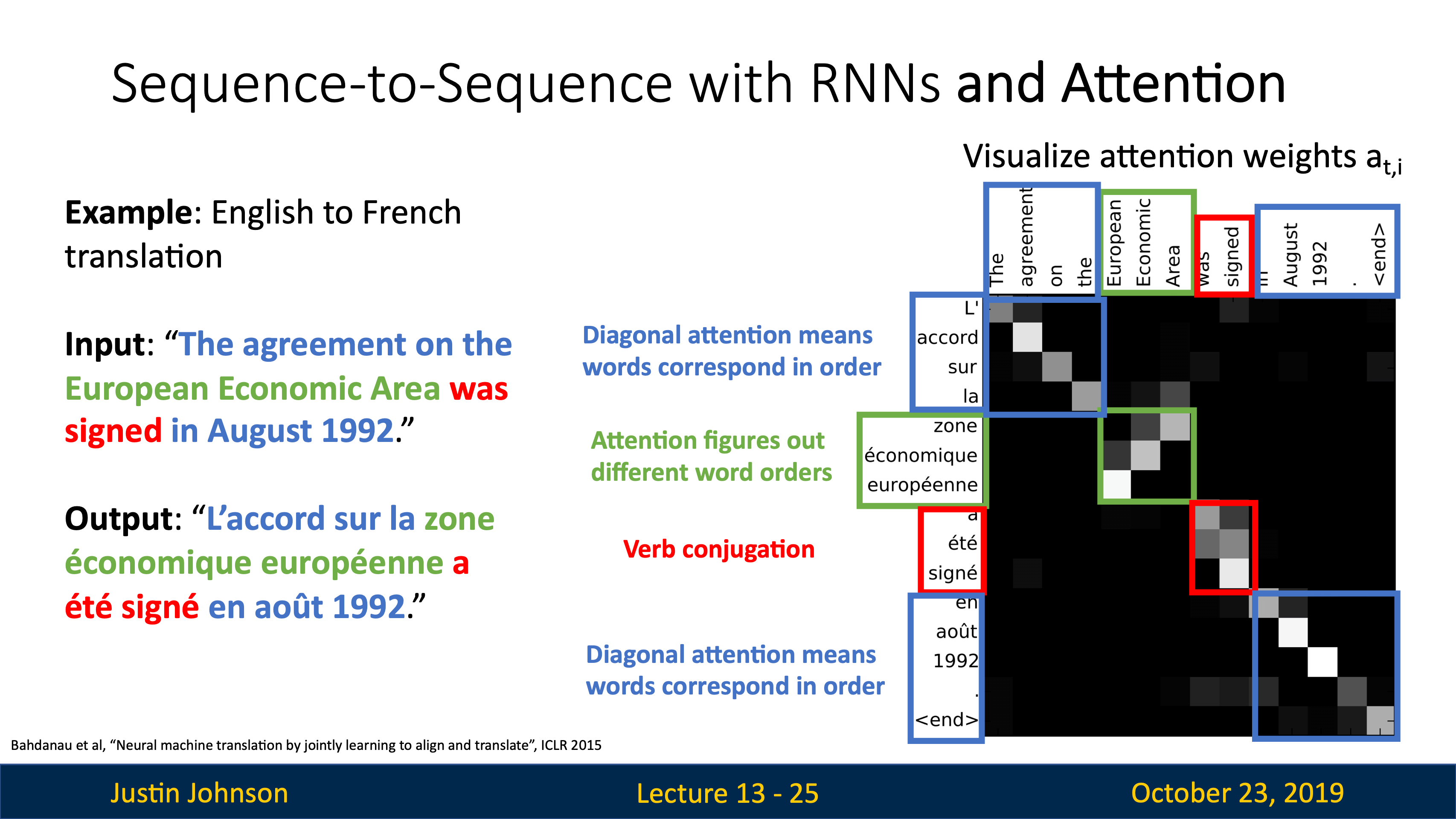
驗證模型是否真的學習到了 Attention 也很簡單,只需要把上面的 probability distribution 即 Attention Weigths 拿出來比一比就可以了。
Visual Attention
| 區別是 probability distribution 從 1D 變成了 2D | 幾乎一模一樣的操作,$h_{i,j}$是個vector,$e_{t,i,j}$是個vector |
|---|---|
 |
 |
跟前面 input 是個 sequence 的區別是這裡的 input 一直是這個 feature map,只不過不同的 time step 關注不同的位置。
這裡跟2017年講的attention很像,就是跟新的 rnn attention idea 結合了一下。
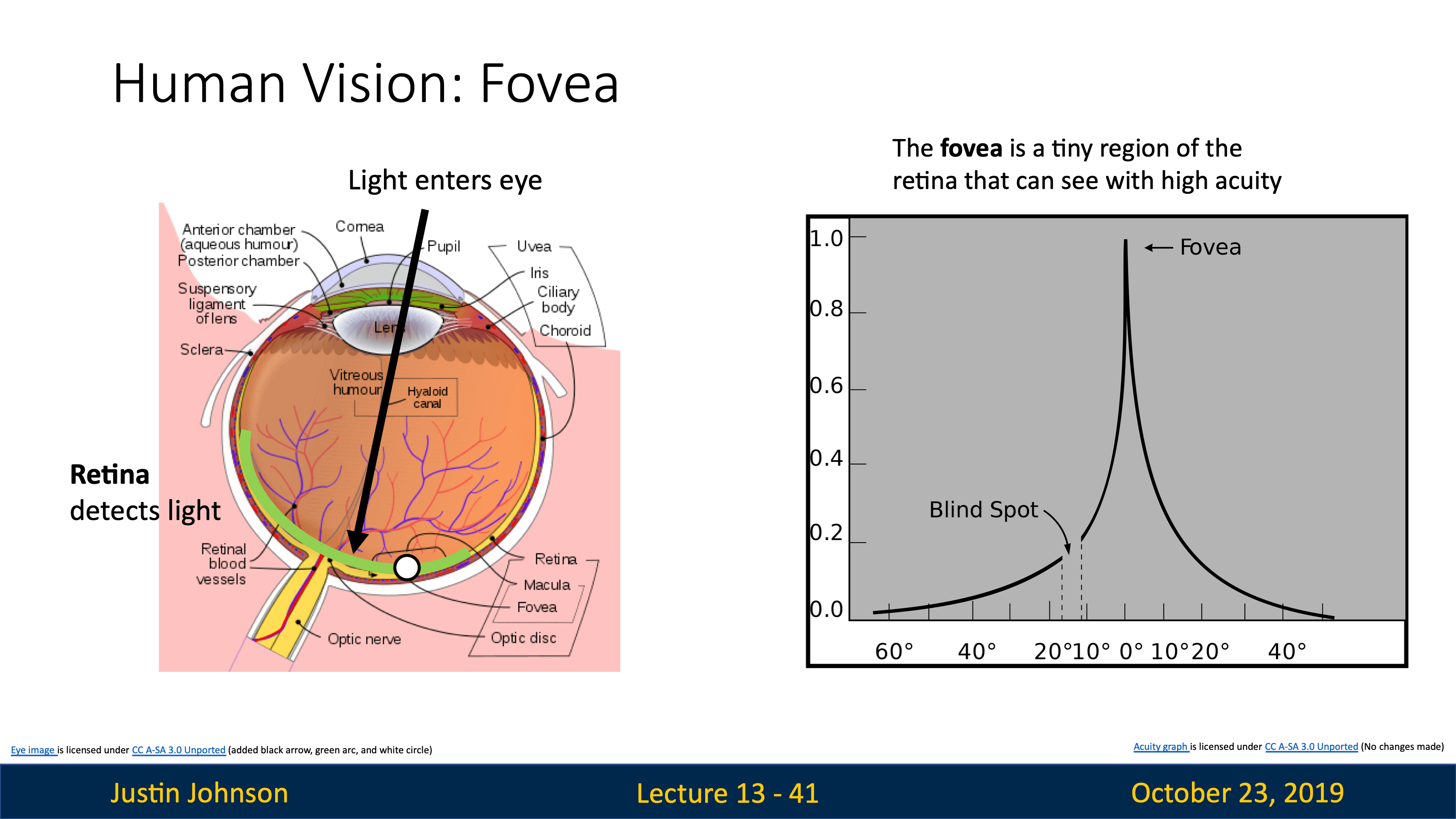
原來晶狀體的英文跟透鏡/鏡頭一樣,都是Lens,Retina視網膜中間的Fovea中央凹是最清晰的視覺,看得到最清楚的細節和顏色,越邊緣部位越不敏銳(visual acuity視覺銳度 或 sensitivity敏感度下降)。
而且原來每個人的眼睛都會有扫视运动(saccades),就算在凝視一個地方也會有微扫视(microsaccades),眼睛會每秒跳很多次以應對Fovea這種機制讓Fovea接收更多信息。
理解論文title
X, Attend, and Y
“Show, attend, and tell” (Xu et al, ICML 2015) 比如這第一篇attention文章,意思就是給模型show一個數據,讓它attend關注某個區域,然後tell通過生成words,告訴你模型看到了什麼。
Look at image, attend to image regions, produce question
“Ask, attend, and answer” (Xu and Saenko, ECCV 2016)
“Show, ask, attend, and answer” (Kazemi and Elqursh, 2017)
Read text of question, attend to image regions, produce answer
“Listen, attend, and spell” (Chan et al, ICASSP 2016)
Process raw audio, attend to audio regions while producing text
“Listen, attend, and walk” (Mei et al, AAAI 2016)
Process text, attend to text regions, output navigation commands
“Show, attend, and interact” (Qureshi et al, ICRA 2017)
Process image, attend to image regions, output robot control commands
“Show, attend, and read” (Li et al, AAAI 2019)
Process image, attend to image regions, output text
總之如果我們想用一個類型的數據來生成另一個類型,都可以考慮用attention mechanism,比如這裡的machine translation和image captioning。
然後就是generalization,有了個很好的mechanism之後,想要把它應用到所有任務。
Abstract Attention Layer, Self Attention
把這個模式推廣。這裡 generalization 的目的不是再用回之前的 RNN,只是因為效果好所以想推廣到所有地方成為一個類似於 FC / Conv 的新的 Layer。
對比下面兩種表達方式:
 |
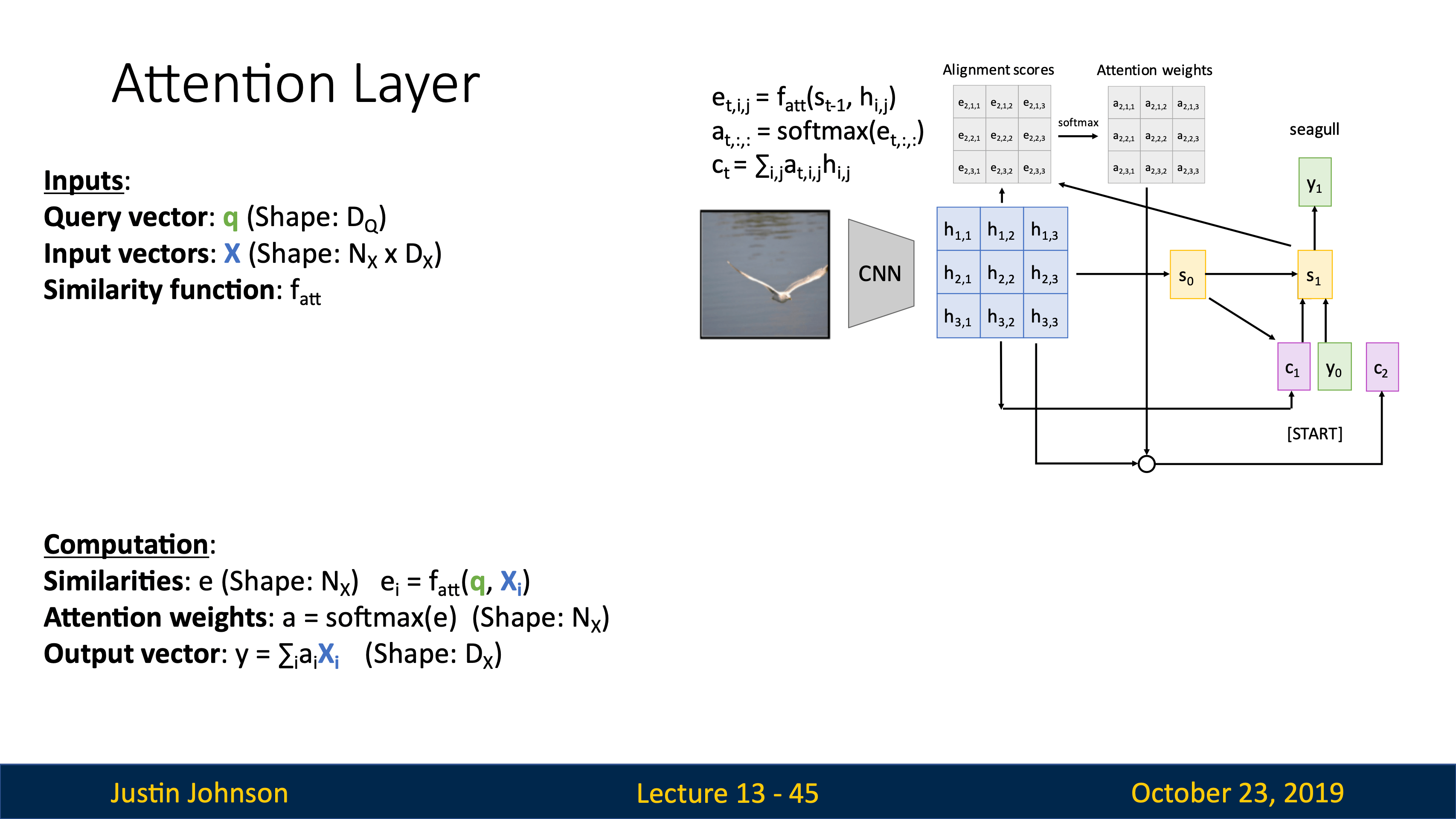 |
- Query vector 對應 Decoder 的 each time step 生成下一個 c 用的 Hidden State vector $s_{1/2/3/4…}$;
- Input vectors 對應 Encoder 的所有 Hidden State vectors $h_{1/2/3/4…}$,有 N 個 inputs;
- 之前 intuition 是 alignment 的函數在這裡叫 similarity ;
- 這個改進可以參考machine translation和image captioning和上面的 “Visualize Attention Weights”,decoder 的 output 跟 input 的區域基本上會有一一對應的關係,可以說就是尋找高維語義空間裡相似的部分;
- 也許沒有一一對應關係的任務需要用回 nn 作為 function approximator,或者針對任務定義 similarities function 。
- e (similarities) 就是之前的 alignment scores ;
- Attention Weigths 沒變;
- Output vector 對應 $c_{1/2/3/4…}$。
改進思路:
- 既然是計算 similarities,可以把 $f_{att}$ 這個 Fully-connected net 變成簡單的 dot product 點積相似度;
- 改進版 scaled dot product,除以 $q$ 和 $X_i$ 的維度 $D_Q$ 的 square root ,總之就是防止 similarities 太大;
- 不讓每一個 $s_t$ 和 $c_t$ 依賴於 $s_{t-1}$ 了,一次用所有 $s_t$ 即所有 Query vectors 矩陣乘 Input Vectors,Simultaneously 。
- 因為 Input vectors 同時用來計算 similarities 和後面的 weighted sum ,所以可以把它分為 K 和 V,Intuition 是跟 BN 加兩個學習參數一樣用來增加 flexibility:
- model 計算 similarities 本來是用 FC 計算,換作點積之後可能減少了靈活性,用一個可學習的 $Weight_K$ 再給它增加回來;
- model 利用 inputs 可能不只是 weighted sum 一種方式,就再加一個 $Weight_V$ 。比如用 Query 搜索時,我們不一定只希望知道 Query 本身,還希望知道跟 Query 相關的其他發散,有 flexibility 就可能給我們返回其他沒有出現在 Query 裡但我們同樣想知道的事。
- 最後/最上面的計算方法是 $Y_1 = V_1 \cdot A_{1,1} + V_2 \cdot A_{1,2} + V_3 \cdot A_{1,3}$。
| 1. 點積 | 2. Query 擴展 | 3. X 轉化爲 K 和 V 分別用在兩個不同計算裡 |
|---|---|---|
 |
 |
 |
上面說的 “不讓每一個 $s_t$ 和 $c_t$ 依賴於 $s_{t-1}$ 了” 本來就有點奇怪,因為 Hidden State 按理說是 Sequential 的,self-attention 就是讓 Query 直接由 Inputs X 生成,用再一個新的 $Weight_Q$,我自認為的 Intuition 是:本來 teacher forcing 時 Decoder 裡所有的 Input 就都是 Groud Truth,不如直接用跟 Y 對應的 X 生成 Query(一開始 RNN 裡的 Hidden State)。
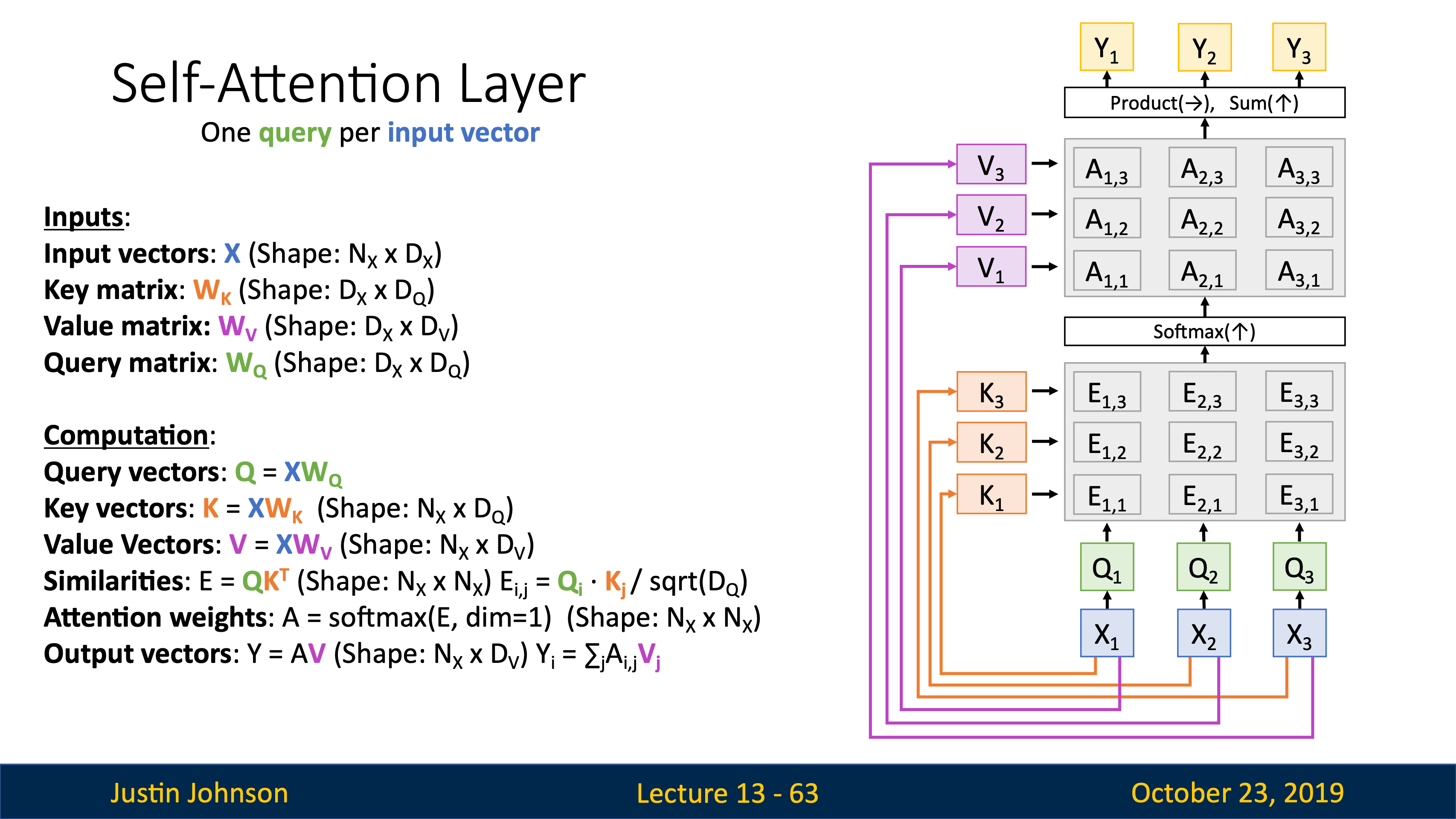
然後就得到了 super generalized layer,(Again,這裡 generalization 的目的不是再用回之前的 RNN,只是因為效果好所以想推廣到所有地方成為一個類似於 FC / Conv 的新的 Layer)
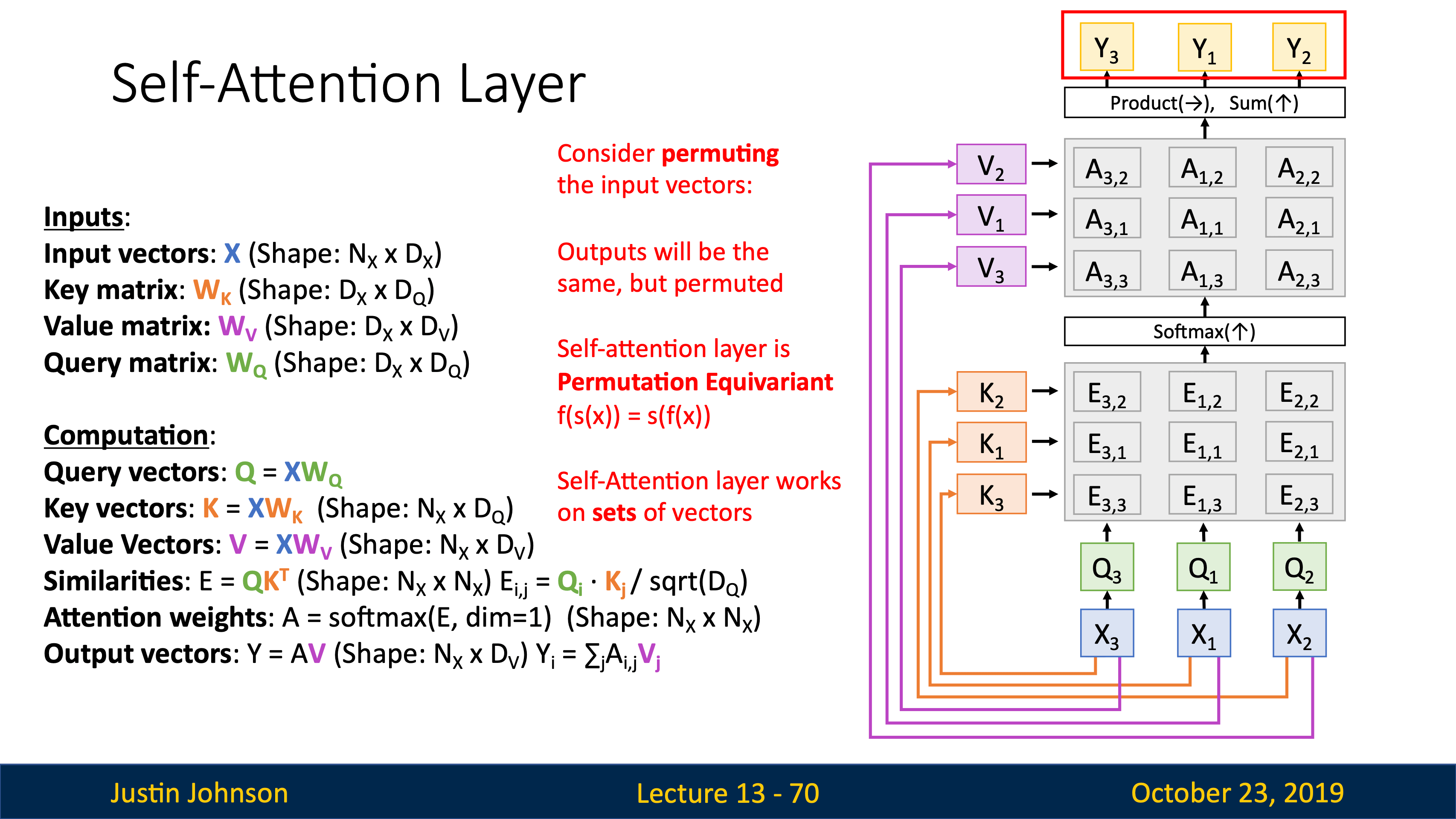
但是這裡其實 layer 感受不到 inputs 的順序,交換 inputs 對輸出沒有影響,只是改變了輸出順序,因為這種計算基本是在讓 input 自己跟自己對比得到結果,有幾種方式(variatns)能讓模型有位置信息:
1. Positional Encoding
可以加入 positional encoding。
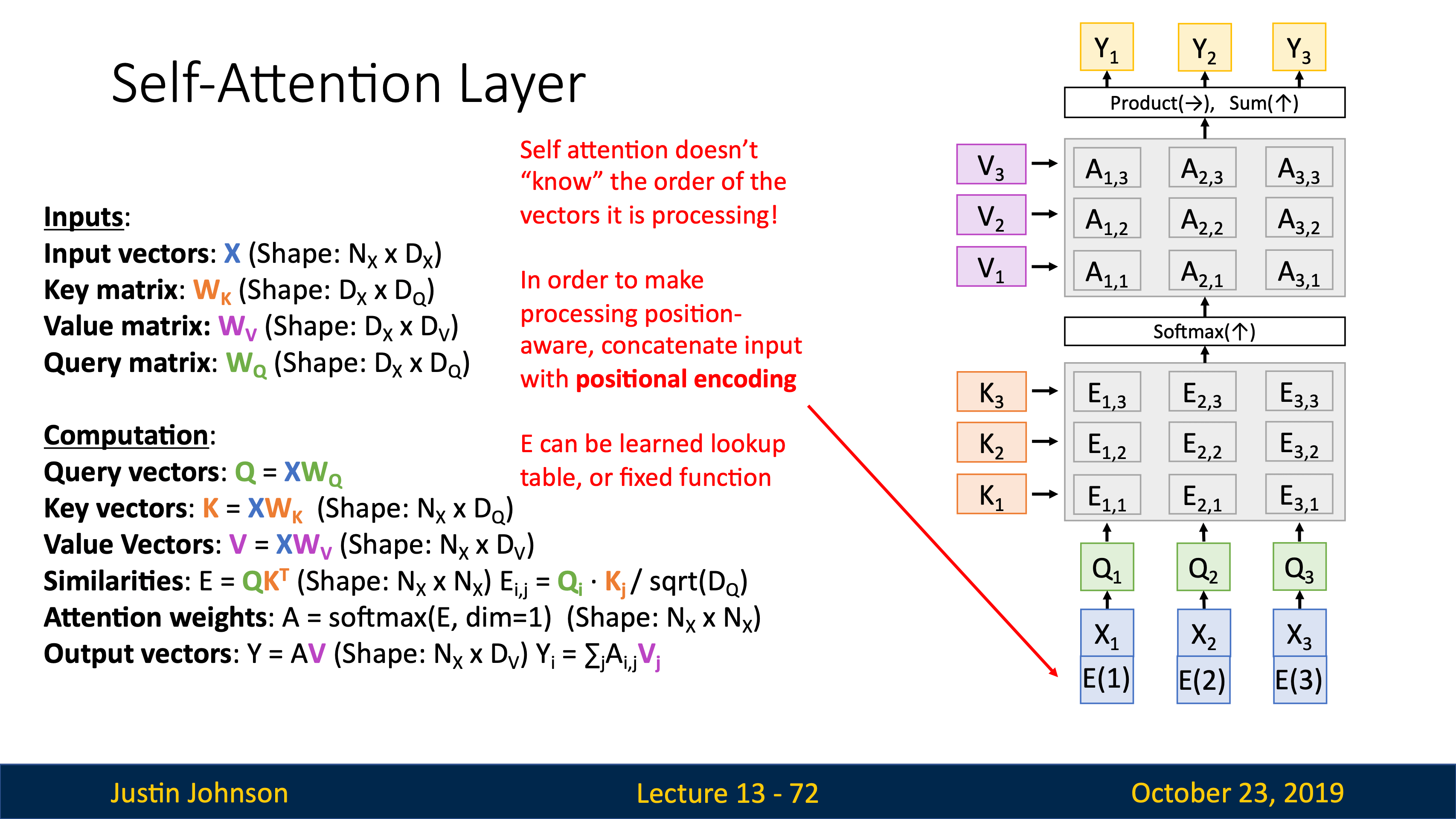
ass 裡加入的方式是用 sin 和 cos 函數映射到 -1 到 1 之間,生成的看起來都是沒有邏輯的隨機數,但說是因為對坐標 i 和 j 引入週期性變化的步長和幅度有助於學習位置關係。
直接加 i 和 j 好像也沒有很好的辦法?
2. Masked Self-Attention
Masked Self-Attention Layer 回到了之前的 RNN attention,又“讓每一個 $s_t$ 和 $c_t$ 依賴於 $s_{t-1}$”,不過牛在可以並行計算,下一個位置的 input 只能利用 the past inputs 的信息,置 $-\inf$ 可以讓 attention weights 為 0,即被 Masked。
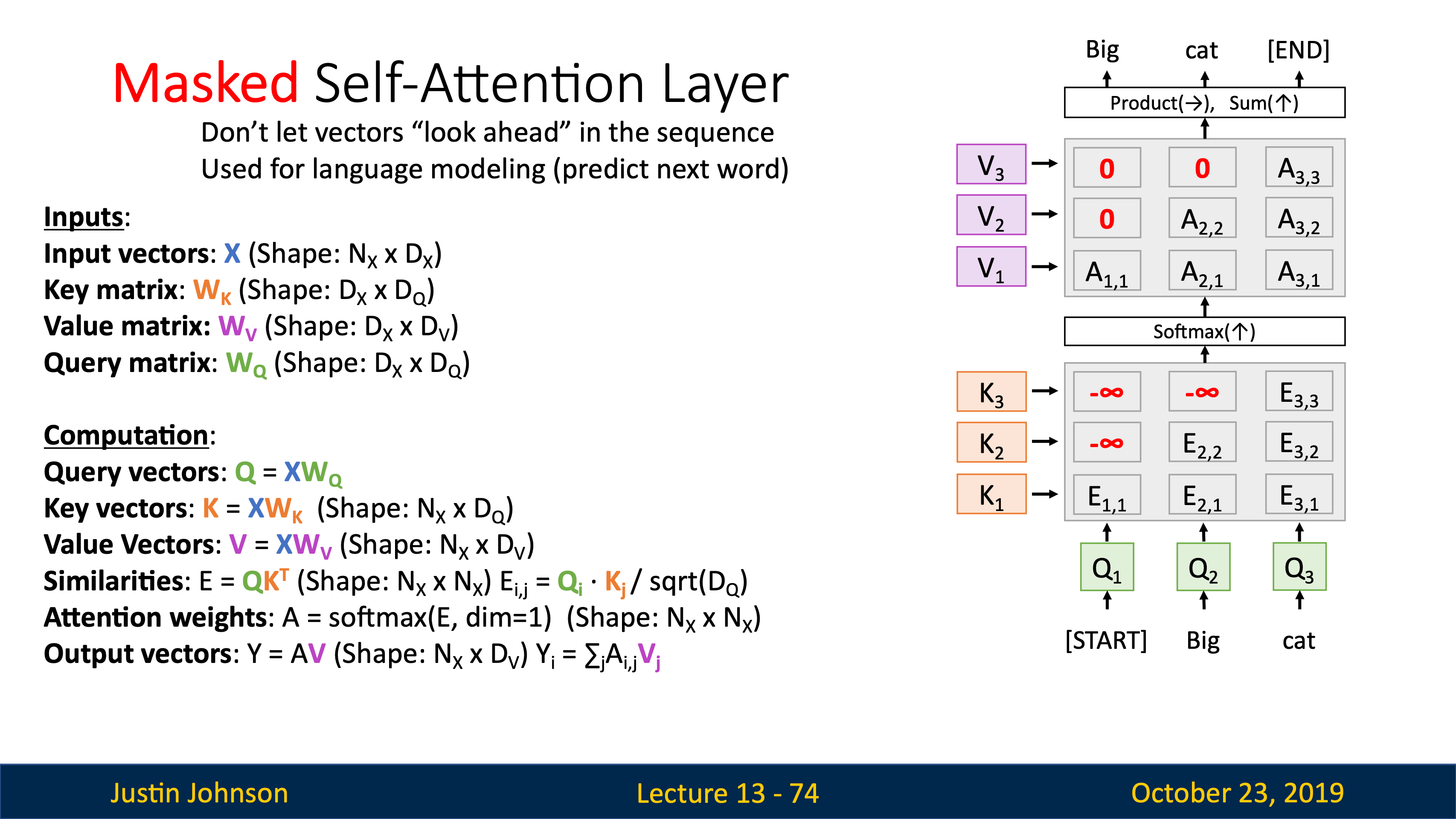
在 language modeling tasks 裡很常用,因為能識別語序。
3. Multihead Self-Attention
步驟是,把 $X_1$ 分成 H 份,把 $X_2$ $X_3$ 都分成 H 份,分別用 H 個 self-attention layer 計算 Y,最後把 H 個結果 concatenate 到一起得到最終的 Y。
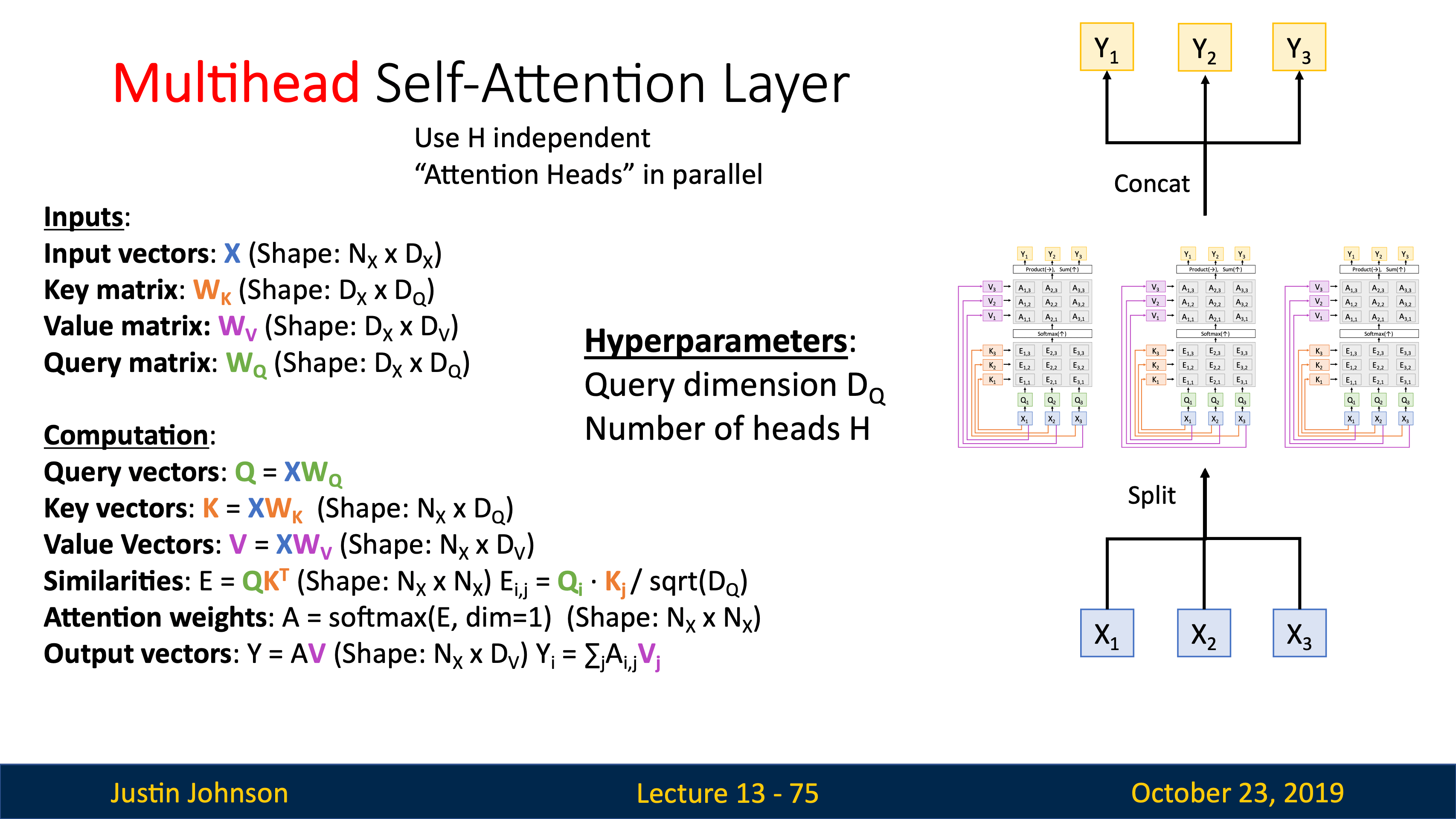
2 個 Hyper Parameters,Query 和 Key 的維度 $D_Q$ 和 #Heads 。多頭也很常用。
Question:Dv怎麼設置?
Layer Example
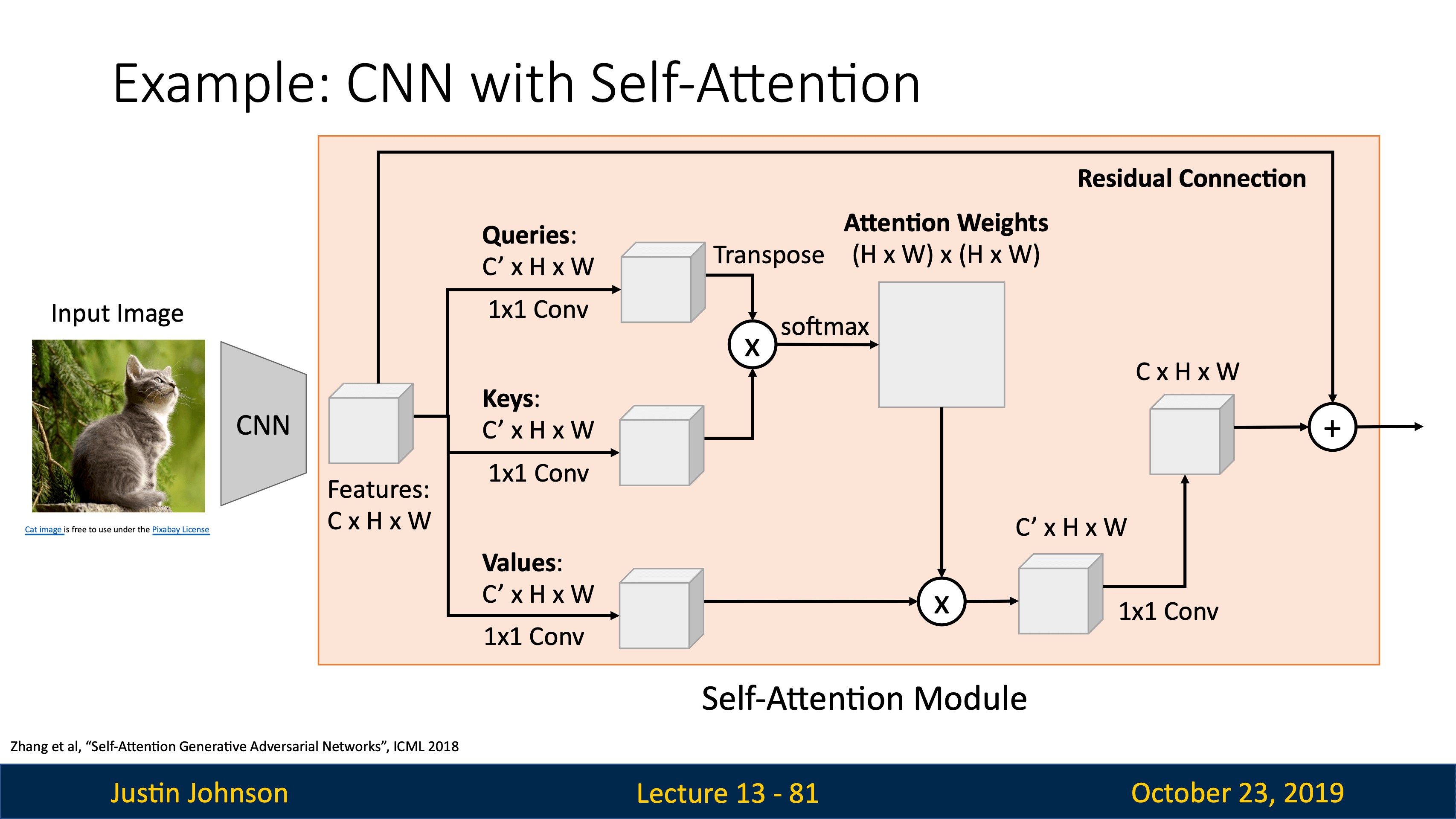
這裡 Attention Weights 的 Intuition 是,Input 的每一個位置有多關注 (attend) 其他 Input 的所有位置。這樣跟 Values 相乘計算的 Y 依賴於 Input 所有位置。
跟 Conv 的卷積和 FC 的純粹 Weighted Sum 都是有點類似的思路,但是完全不一樣的計算方法, a very different type of computation。
這就是一個完全不同的層,比如我們可以 Conv x N — Self-Attention x N — Conv x N — FC x N 這樣搭新的積木。
Comparison
 |
 |
self-attention 的需要很多 memory 存參數的問題,對現在的 GPU 不太是大問題。
對 sequence 問題來說,Attention is all you need,不需要考慮 LSTM 和 CNN。2017 年這篇文章用 self-attention layer 設計了 Transformer Block,
| 因為這些independency,所以transformer的擴展性和并行性都特別好—— | scalability和parallelism性質好是相輔相成的,因為不像lstm一樣依賴序列順序計算,所以並行性好,矩陣在 GPU 的並行高效運算提高了效率,也就讓模型可以擴展到更大模型和更長序列。 |
|---|---|
 |
 |
- Layer Norm 做的是 normalize each of the output vectors from self-attention independently,效果很好;
- 每一個 MLP 也是會 independently 處理每個 output vector;
- residual 讓梯度流更 clean 的做法仍然很好用,MLP 之後也是一樣加個 Layer Norm。
在已經忘記 Transformer 結構的前提下,我做的之前 ass2 的實驗,batch norm的好結果跟後來模型的選擇也確實是不謀而合。
從 Transformer 開始,CV裡常用的Pretrain-Finetune模式也開始大規模發生在NLP領域,2017年發表了Transformer,2018年各大AI Lab都開始competing訓練bigger and bigger and bigger transformer models,Layers、Width(Dq)、Heads都大幅增加。Data雖然是40G但是對text來說已經很多很多了。
這裡的公式好像寫錯了?Key和Value應該是同樣維度,而Query是不同維度?Aij的求和方式也不太對,但是代碼裡其實沒有顯式地求和。
Google Facebook OpenAI Nvidia Megatron 變形金剛到霸天虎?OpenAI當時的文本生成就做得很好。
Lecture 18 Self-Supervised Learning
剛寫完 GANs 先用 Generative 任務跟 Self-supervised做個對比:
- 兩者目標都是從沒有 人工標注的數據 (data without manual label annotation) 中學習。
- 區別:
- generative learning 目標是學習到 $p_{data}(x)$ 這個數據分佈,比如 VAE 就是直接學習正態分佈的 mean 和 variance 來採樣足夠真實的生成數據。
- self-supervised learning 目標是通過解決 “pretext” tasks 來產生足夠應付 下游任務(downstream tasks) 的 features;
- training 的時候實際上還是用 supervised leanring objectives,還是用 classification 或 regression 任務;
- 這些“預訓練任務/預文本任務” pretext tasks 的 labels 都是自動生成的。

就像這個經典例子,證明人類只通過記住一些顯著要素 salient aspects 來認知世界,
- 根本不需要學習到能畫出 / generate pixel-level details 的地步,
- 學習 high-level semantic features with pretext tasks 就足夠了。
| 通過下游任務的表現來評價自監督學習 | 這門課只講了CV的pretext |
|---|---|
 |
 |
The reason SSL methods have seen a surge in popularity is because the learnt model continues to perform well on other datasets as well i.e. new datasets on which the model was not trained on!
Confusion Matrix
Confusion Matrix 混淆矩陣,裡面包含很多很多種 metrics 衡量任務表現的指標,拿這個問chatgpt的gpt4幾次它就算錯幾次。
假設現在做貓狗分類任務,🐱:30只,🐶:70只。
預測結果:
- 識別出🐱20只,其中18只是🐱,2只識別錯了其實是🐶;
- 識別出🐶80只,其中68只是🐶,12只識別錯了其實是🐱;
假設🐱是正例,🐶是負例:
- True Positive: 這裡所有的 True 和 False 都是模型預測正確與否,即是否把🐱分類為🐱把🐶分類為🐶,Positive 和 Negative 是模型預測的類別。
- True Positive: 18只識別正確的🐱;
- False Postive:2只識別錯誤的🐶;
- True Negative:68只識別正確的🐶;
- False Negative:12只識別錯誤的🐱。
最需要記住的其實就是前面這個布爾值是“評估”模型是否正確,後面這個正負量是模型“推理的結果”。
然後其他所有的 Measures 找一個基準點就好理解,用最熟悉的“準確率”Accuracy作為參照物:
- ACC = (TP + TN) / (P + N),準確率,分子是兩個 T,分母是所有樣本,也就是所有數據裡模型預測對的比例,模型最直觀的能力。上面的例子就是 86%。
- Recall,有的地方叫Sensitivity敏感性,= TPR = TP / (TP + FN) = 分類正確的🐱 18 / 所有真正的🐱 30 = 60%。有時我們只關心能不能把貓貓🐱全給找出來,所以只對正例🐱算的acc準確率就是召回率。
- 癌症推斷場景是很好的例子,我們希望所有的癌症陽性患者都被檢測出來,寧錯殺不放過;
- 商湯的垃圾桶滿溢做了半年過去兩年我現在才理解,我們關心的是所有滿的垃圾桶都要報警防止污染環境,不那麼關心有沒滿的垃圾桶被預測為滿的讓人空跑一場(反正半滿也能先清一下)。
- Precision,有時跟acc會混叫準確度,其實該叫精度,Positive Predictive Value, PPV = TP / (TP + FP) = 分類正確的🐱 18 / 所有被分類為🐱的🐱和🐶 20 = 90%。
- 還是上面那個場景,在滿足了高召回率recall之後,我們也希望precision高,即希望不要把健康人分類為癌症患者。
- Specificity, SPC = TN / (FP + TN) = 分類正確的🐶 68 / 所有真正🐶 70 = 97%。
- 這個跟recall類似,就是關心把所有🐶給找出來;
- 也可理解成跟precision一樣關注假陽性(FP)儘量少。
- F1 score = 2TP / (2TP + FP + FN)
- $F1 = \frac{2 \times \text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}}$
- 是精度和召回率的調和平均數,調和平均數就是倒數的平均數:
- $F1 = \frac{2}{\frac{1}{\text{Precision}} + \frac{1}{\text{Recall}}}$
- Intuition就是希望在recall和precision之間找個平衡,既希望把所有的🐱找出來,又希望不要把🐱錯分為🐶;既希望不論對錯把所有疑似癌症患者找出來,又希望別把太多健康人錯診,一個平衡量。
- F1這種“平衡”為什麼不能直接用ACC?因為 ACC 的分子有 TN 🐶,F1 只有 TP 🐱。
- 癌症篩查裡,正負樣本不平衡,癌症人數遠遠少於正常人數,模型會通過正確預測健康人群 (TN) 提高準確率,ACC也會變大。
- AUC-ROC, Area Under Curve Receiver Operating Characteristic,評估二分類模型,反正值域
[0, 1]越大越好。- ROC適用於均衡或不均衡的數據集分類;
- Precision-Recall 更適用於不均衡數據集,這個曲線可能是各種樣子,precision和recall也可能同時為1。
 |
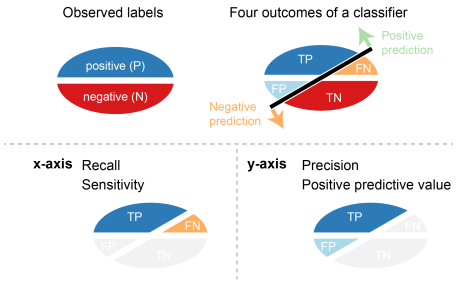 |
- IoU(Intersection over Union):用于目标检测和分割任务,衡量预测框和真实框之间的重叠度。
- $\text{IoU} = \frac{\text{预测区域} \cap \text{真实区域}}{\text{预测区域} \cup \text{真实区域}}$
- % mAP(Mean Average Precision)平均精度,mAP 评估的是检测或分类模型的精度。
- AP是算上面說的 Precision-Recall 曲線下面積 PR-AUC;
- mAP是求不管正負例雞鴨鵝狗例的,所有類別AP均值。
- % mIoU(Mean Intersection over Union)平均交并比,mIoU 评估的是分割模型的质量。
- 對每個類別計算IoU;
- 計算所有類別平均IoU。
Agenda:
- Pretext tasks from image transformations
- Rotation, inpainting, rearrangement, coloring
- Contrastive representation learning
- Intuition and formulation
- Instance contrastive learning: SimCLR and MOCO
- Sequence contrastive learning: CPC
Pretext tasks from image transformations
現在的驗證碼,不是讓人旋轉圖形,就是讓人拼圖,或者讓人組合打亂的字,再不然就是既旋轉又拼圖又排列組合。跟這些pretext tasks一毛一樣。

rotations
Hypothesis: 一個模型只有具備視覺常識,即知道沒擾動的物體應該是什麼樣子,才能正確識別物體的旋轉。
可以不當作 regression 判斷旋轉度數,而是只用 4 種旋轉方式。
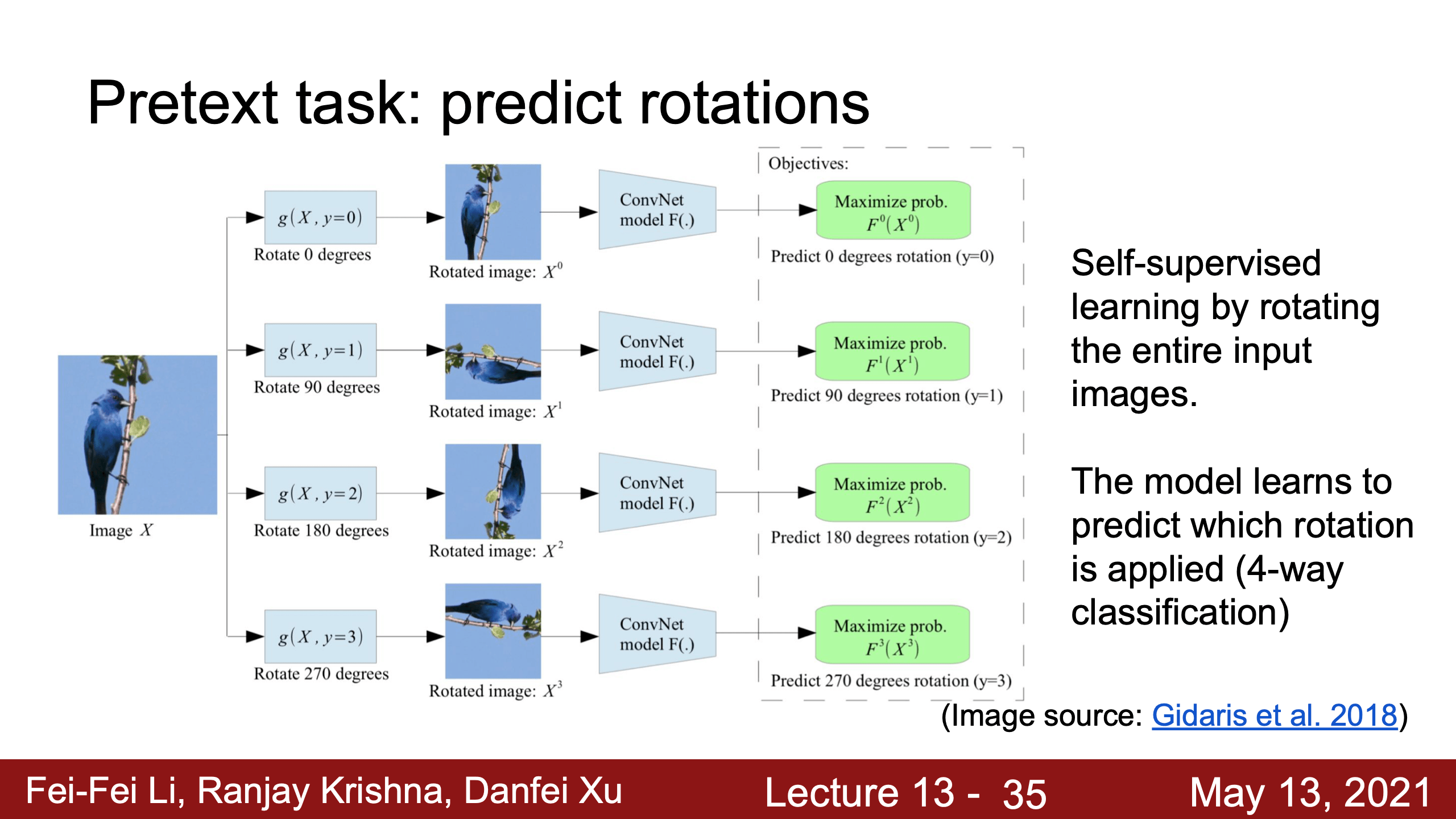
做法是在 CIFAR10 整個數據集上自監督訓練,然後下游任務比如 classification 就 freeze 前兩層 conv1 conv2,只用一個 CIFAR10 的子集 fine tune 後兩層 conv3 linear。
最終大規模跑的實驗是用 AlexNet 在整個 ImageNet 自監督訓練,在 Pascal Voc 2007 上 finetune 了 classifcation(%mAP)、detection(%mAP)、segmentation(%mIoU) 三個任務。
inpainting
圖像填充 / 圖像修復。
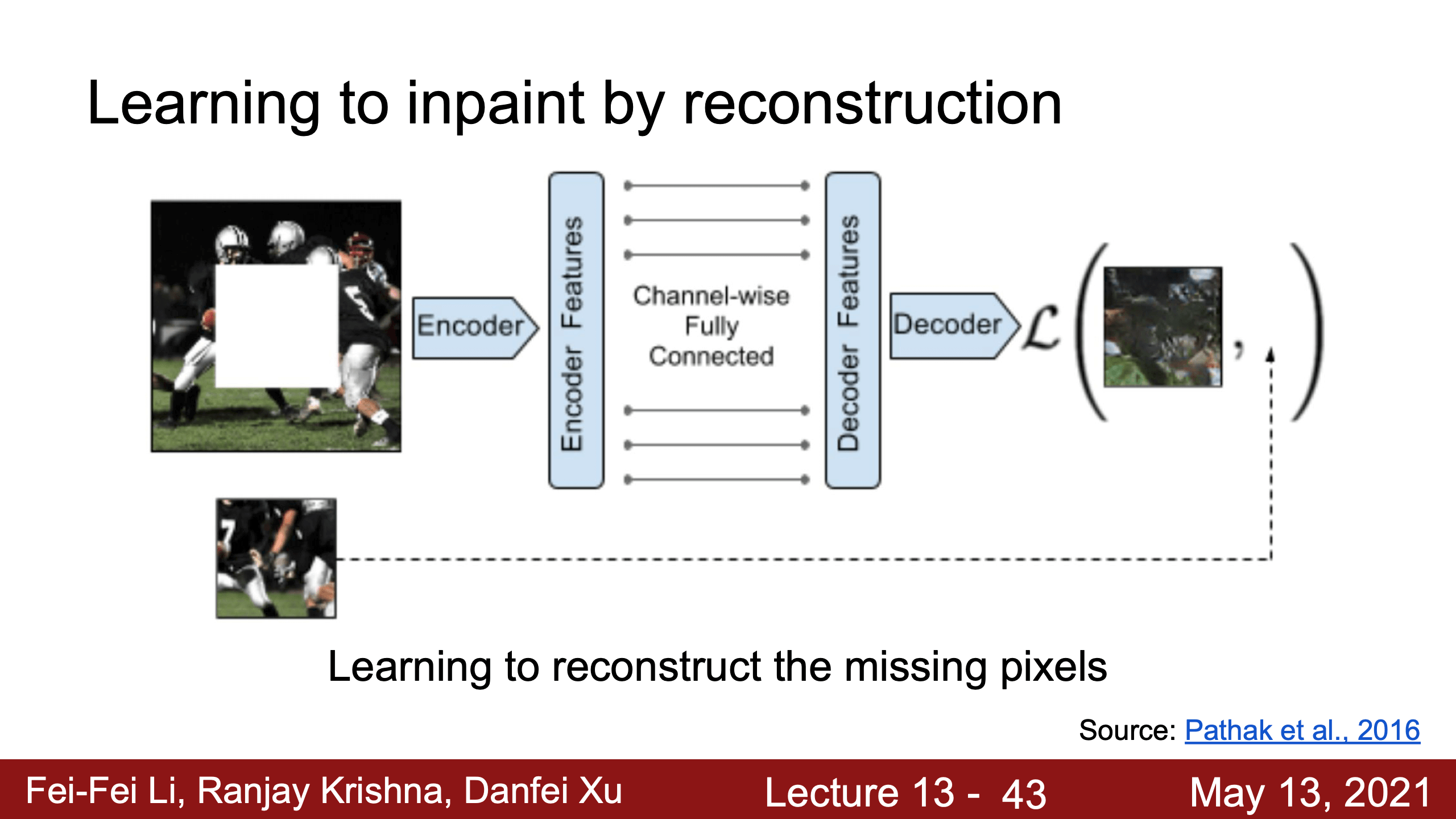
Adversarial loss between “real” images and inpainted images,先用重建損失訓練generator,然後用對抗損失的半部分加強這個loss $L_{\text{adversarial}} = - \log D(\hat{I})$ 。
rearrangement
| 判斷patch的相對位置,predict relative patch locations | jigsaw拼圖,solving jigsaw puzzles |
|---|---|
 |
 |
9個數permutation排列不是一共9!=362,880種嗎?
coloring

通過一個channel預測其他channel的值,最後concatenate到一起。
Contrastive representation learning
上面所有pretext tasks都會導致學習到的特徵綁定在一種任務上,下面這種pretext task可以集合他們所有的perturbation的優勢。(perturb 擾動和 permute 排列別混了)
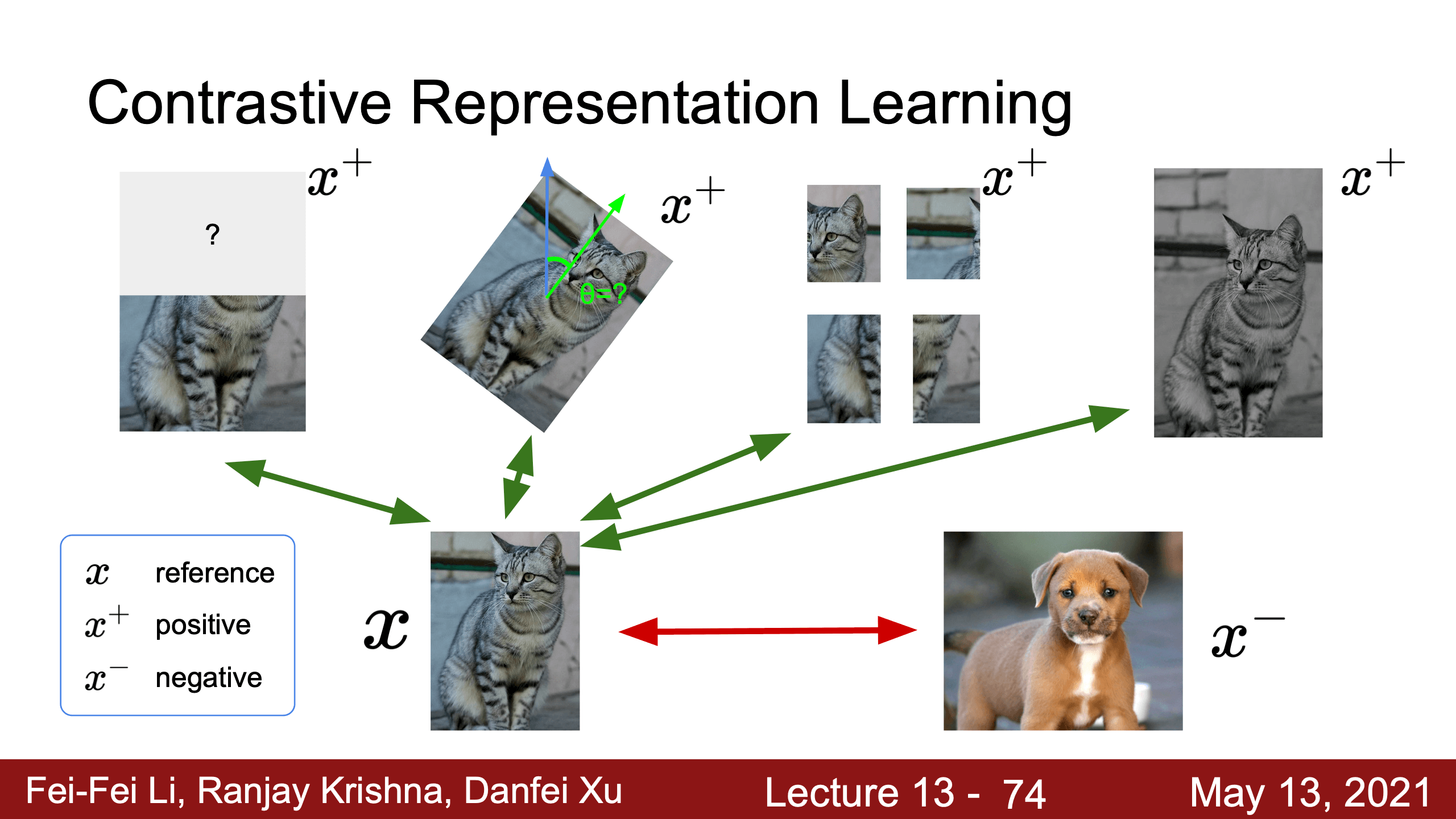
希望所有被擾動的樣本都互相attract,非同一類的樣本都互相排斥repel,可以得到這個pretext task的目標:

綠色的分子和分母代表正例和參照圖的pair,紅色的分母代表其他所有負例和參照圖的pair,這合起來就是一個 Cross entropy loss for a N-way softmax classifier!
代入普通的多分類交叉熵損失,這裡的正負例對應各類別的分數,這個Loss的意思就是試圖從 N 個 samples 裡找到那個正樣本 positive sample。

- 叫信息對比損失InfoNCE Loss是因為基於一個概率模型估計方法Noise Contrastive Estimation (NCE, 2010的paper)。
- 這裡的MI是Mutual Information互信息,即經過訓練後增強的圖片和原圖在特徵空間的距離,我們希望這個值即兩者在表示空間的距離盡可能近。
- 公式的直觀意思是 infoNCE 是 MI - log(負樣本數) 的下界:
- 改成 $\text{MI}[f(x), f(x^+)] \geq \log(N) - L$ 好理解點;
- 增大負樣本 N 數可以讓 增強圖 和 原圖 在特徵空間距離下界更高,即更近、更好。
SimCLR and MOCO
Instance contrastive learning
SimCLR就是設定s為cosine similarity?
| SimCLR, A Simple Framework for Contrastive Learning of Visual Representations, Google | 所有的data augmentation |
|---|---|
 |
 |
我們其實只需要 f 變換之後的特徵 h 用於下游任務,但還是多變換了一次 g,因為這個線性/非線性的 projection head 提升了特徵學習的效果。
- paper的4.2. A nonlinear projection head improves the representation quality of the layer before it和B.4. Understanding The Non-Linear Projection Head講了加這個 投影頭 的好處。
| projection head | projection |
|---|---|
 |
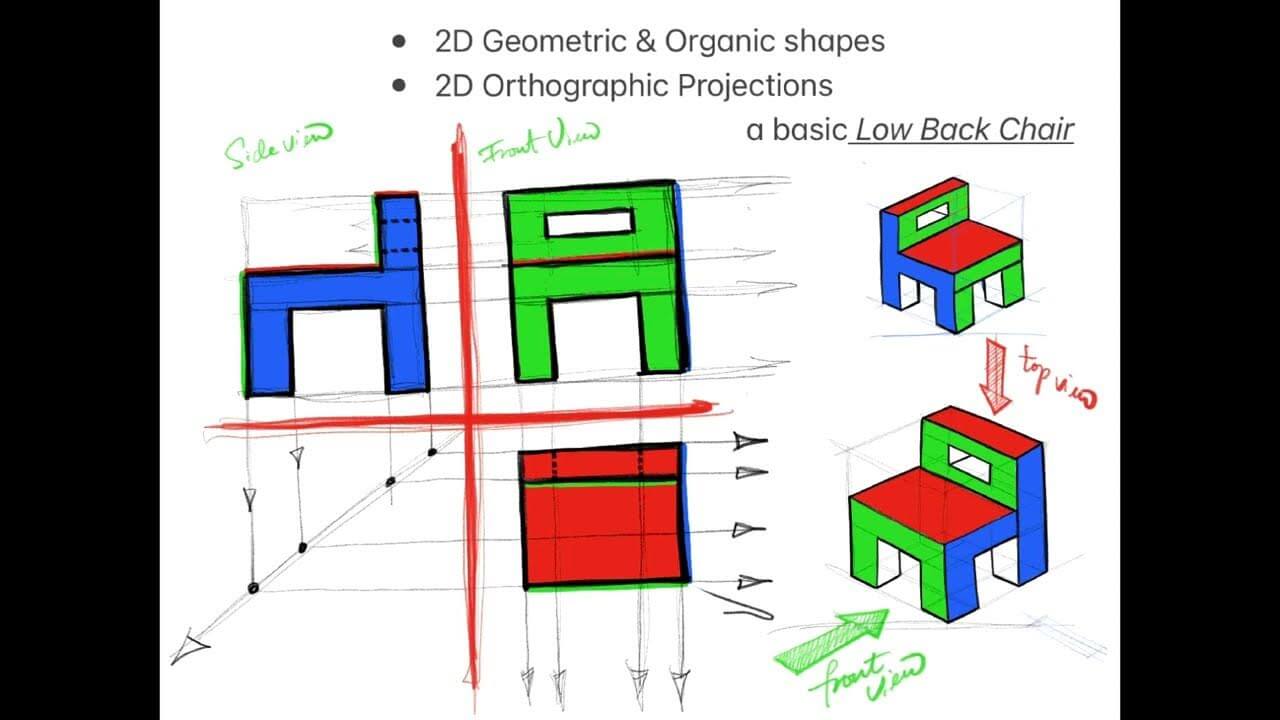 |
- 為什麼叫projection head,我理解就是個降維操作,類似PCA和t-SNE,投影本身就是一種降維,這些都在降維裡復習,而且 f(x) 是個很深的網絡 like resnet,g(h) 只是個簡單的MLP,又因為在其他網絡頂上,所以叫投影頭;
| pseudo code | assignment3最後一個作業實現方式跟 paper 不一樣,這個公式更容易寫代碼 |
|---|---|
 |
 |
寫 ass 的時候能感覺到,sim_matrix = compute_sim_matrix(out) # [2*N, 2*N]
sim_vector = sim_positive_pairs(out_left, out_right) # (N, 1)
這裡有個問題,根據上面的 $\text{MI}[f(x), f(x^+)] \geq \log(N) - L$ 可以知道,負樣本越多特徵學得越好,
simclr 文章中提到,
To keep it simple, we do not train the model with a memory bank (Wu et al., 2018; He et al., 2019). Instead, we vary the training batch size N from 256 to 8192. A batch size of 8192 gives us 16382 negative examples per positive pair from both augmentation views. Training with large batch size may be unstable when using standard SGD/Momentum with linear learning rate scaling (Goyal et al., 2017). To stabilize the training, we use the LARS optimizer (You et al., 2017) for all batch sizes. We train our model with Cloud TPUs, using 32 to 128 cores depending on the batch size.2
As the loss, we use NT-Xent, optimized using LARS with learning rate of 4.8 (= 0.3 ×BatchSize/256) and weight decay of 10−6.
最後選擇的是 We train at batch size 4096 for 100 epochs. ,縮小 batch size 會讓 performance 變差。
一次計算完 batch (e.g. 4096 張) 裡所有元素的 sim_matrix 開銷很大,2 個 augmentation 之後變成 8192 張,每個 minibatch 算 sim_matrix 都需要 8192x8192=67108864 ops。
而 moco 文章中提到,他們在 ImageNet 1K 的 ~1.28M imgs 1000 classes 和 Instagram 的 ~940M imgs ~1500 hashtags 數據集上的選擇是,
Training. We use SGD as our optimizer. The SGD weight decay is 0.0001 and the SGD momentum is 0.9. For IN-1M, we use a mini-batch size of 256 (N in Algorithm 1) in 8 GPUs, and an initial learning rate of 0.03. We train for 200 epochs with the learning rate multiplied by 0.1 at 120 and 160 epochs [61], taking∼53 hours training ResNet-50. For IG-1B, we use a mini-batch size of 1024 in 64 GPUs, and a learning rate of 0.12 which is exponentially decayed by 0.9×after every 62.5k iterations (64M images). We train for 1.25M iterations (∼1.4 epochs of IG-1B), taking∼6 days for ResNet-50.
對 IG-1B 選用 batch size 1024,假如跟 simclr 一樣負樣本 size 也是 4096 (queue size K),那麼根據下面 pseudocode,
- 首先這裡不是計算 4096x2=8192 個負樣本,query 也是 1024 而不是 2048;
那麼 sim_matrix 總操作就是 query(batch size)*queue(K)=1024x4096=4194304,每個batch小了一個數量級;
跟 simclr 一樣,比如 batch size 256,ref img 是 🐱,就算剩下 255 imgs 裡有 🐱 也會被當作負樣本,這個似乎是 self-supervised 無法解決的問題?
但是如果 batch size 都選用 4096,K 選用遠大於 batch size 的 65536,那麼其實一個 batch / iteration / epoch 的計算量 moco 是大於 simclr 的,我認為 moco 的主要優勢在於,
- 這其實是 memory bank 的優勢,每個 batch 接觸到的負樣本比正樣本多很多,從比例上看更多操作量分配到 repel 負樣本上了,更少 attract 正樣本,從結果上看效果更好;
- 一個 batch 的正樣本和負樣本都來自 momentum 更新的 f_k,ref img 本身是生成自 f_q,前期更新速度慢,訓練穩定,負樣本特徵空間的噪聲小:$\theta_{\text{momentum}} \leftarrow m \cdot \theta_{\text{momentum}} + (1 - m) \cdot \theta_{\text{model}}$, theta 設置如下有消融實驗。

 |
 |
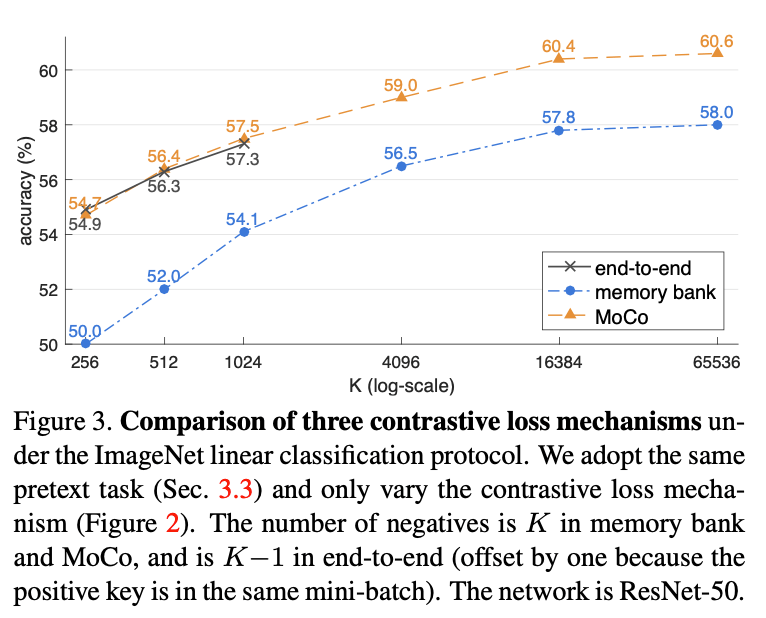
moco 對比 memory bank:
- 對比學習負例越多久越難(正例越多也越難吧),兩者思路都是增加負例,都是解耦 decouple 了 batchsize 和 number of negatives;
- memory bank 是把 f_k 計算過的負樣本 feature 全都存起來作為負例,
- f_k 不變會導致跟 f_q 特徵空間差別太大學到的東西很差,本來希望 🐱 repel 🐶 這種負例,如果特徵空間不一樣 🐶 可能變成了外星 🐱 即 paper 裡講的 consistency ;
- 用 queue 解決內存和計算限制的問題,盡可能多但不是用全部負樣本;用動量更新 f_k 解決了希望負樣本多的情況下兩側 encoder alignment 的問題。
The memory bank mechanism can support a larger dictionary size. But it is 2.6% worse than MoCo. This is inline with our hypothesis: the keys in the memory bank are from very different encoders all over the past epoch and they are not consistent.
| MoCo, Momentum Contrastive Learning (v1居然還是何愷明做的) | pseudo code |
|---|---|
 |
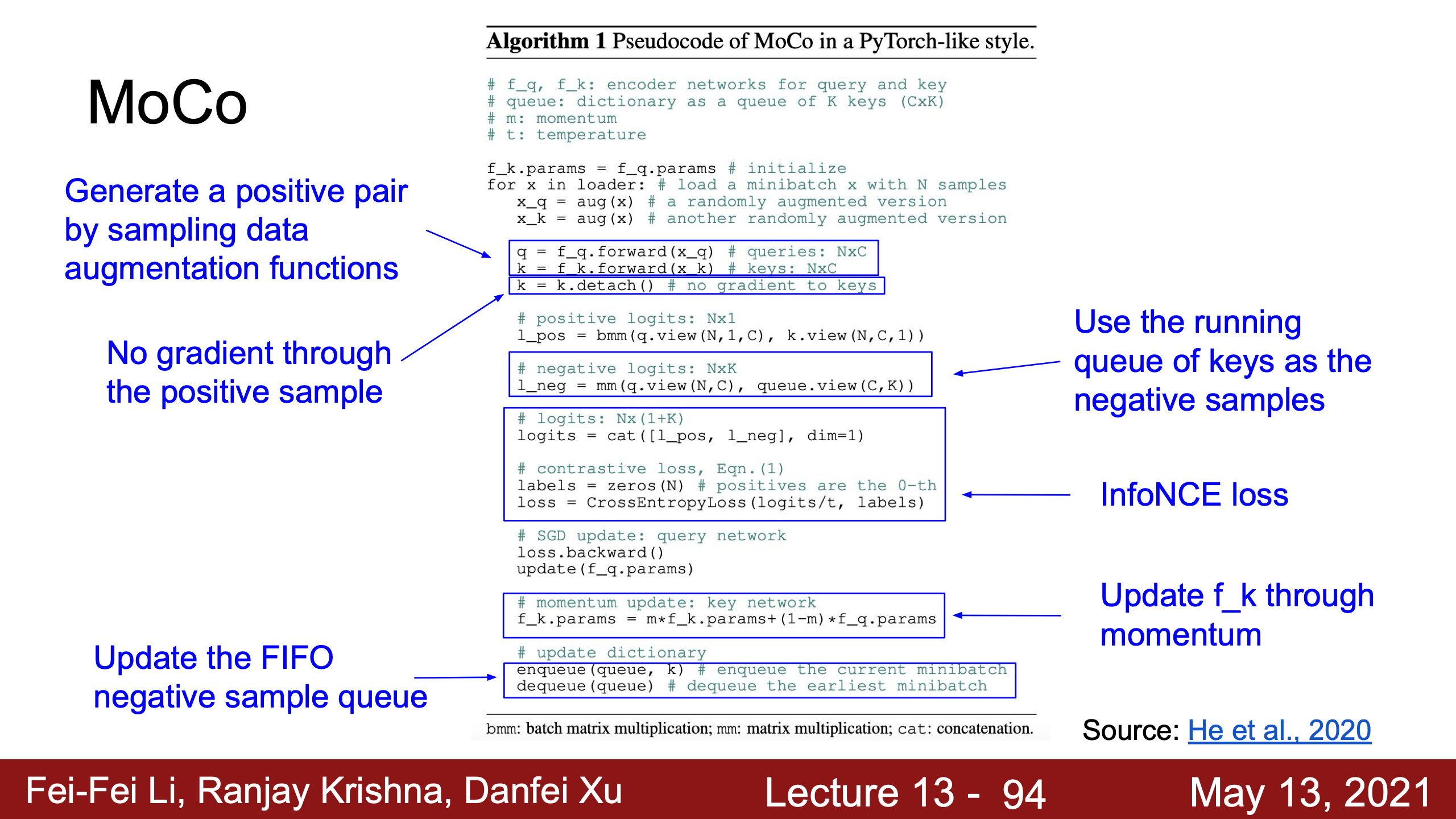 |
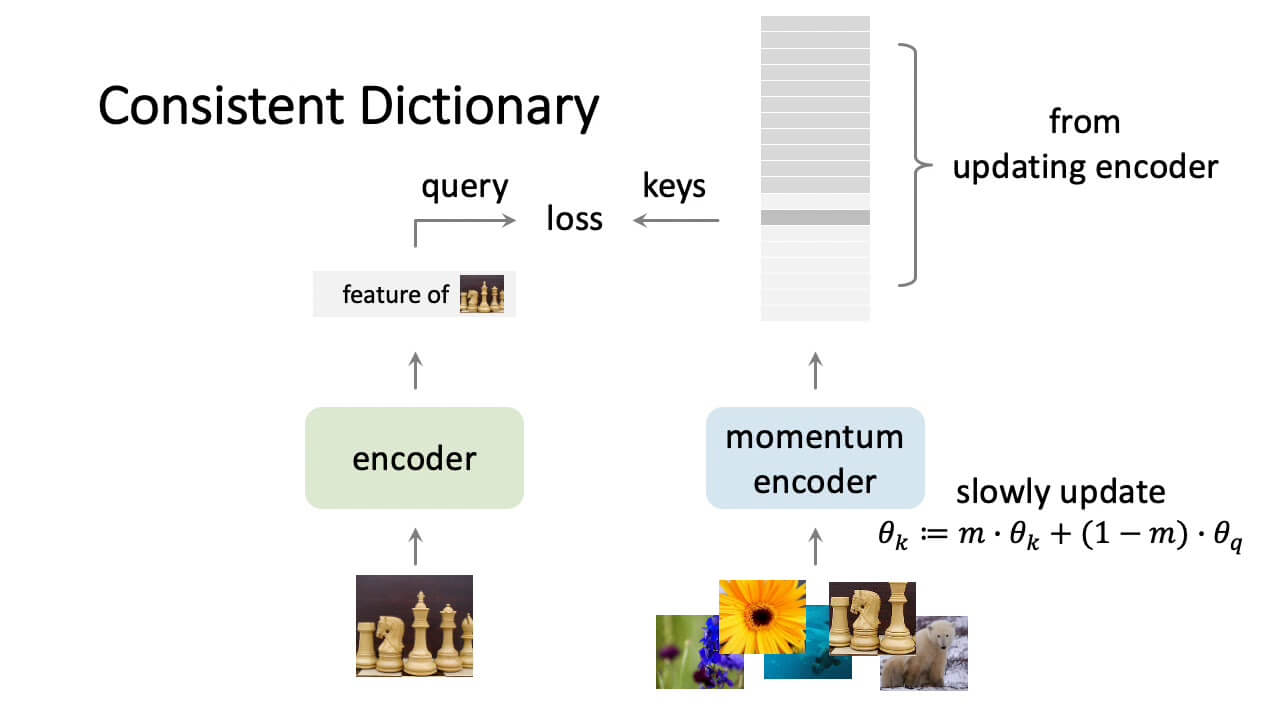
實驗量很大,主要貢獻感覺是工程上的。
想理解模型還是看代碼最快,code 缺實現細節再從論文裡摳。
CLIP
| text vs. img | numpy like pseudocode |
|---|---|
 |
 |
把爬下來圖文配對數據處理一下,每一段文本對應一個圖片,整段文本編碼成 1 個向量表示,是整個句子的 semantic embedding,跟圖片做對比損失。
CPC
Sequence contrastive learning
Bert/GPT/T5
雖然都基於transformer,但pretext task和工程實現差別很大。
1. BERT (Bidirectional Encoder Representations from Transformers)
Pretext Task: Masked Language Modeling (MLM) 和 Next Sentence Prediction (NSP)。
Masked Language Modeling (MLM): BERT 的核心任务是随机遮蔽输入文本中的一些词(即使用
[MASK]标记代替某些词),然后让模型根据上下文预测被遮蔽的词。这个任务使得 BERT 学习到输入序列中每个词的上下文信息。由于它是双向的,BERT 会同时利用左侧和右侧的上下文来做出预测。Next Sentence Prediction (NSP): 这个任务用于帮助 BERT 学习句子间的关系。给定一对句子,模型需要预测第二个句子是否是第一个句子的后续句子。这个任务有助于捕捉句子间的语义关系,尤其对于问答和自然语言推理任务(如SQuAD)很有帮助。
2. GPT (Generative Pre-trained Transformer)
Pretext Task: Causal Language Modeling (Autoregressive Language Modeling)。
GPT 的预训练任务是 因果语言建模,也叫 自回归语言建模。在这种设置中,GPT 的目标是预测序列中每个词的下一个词。具体来说,给定输入文本的前面一部分,模型学习如何生成文本的下一部分。GPT 模型是单向的(从左到右),只利用前面的上下文来预测下一个词。这种任务让 GPT 能够学习文本生成和语言建模的能力。
3. T5 (Text-to-Text Transfer Transformer)
Pretext Task: Text-to-Text Transformation (denoising autoencoding)。
T5 的预训练任务可以看作是 去噪自编码(Denoising Autoencoding)。具体来说,T5 将所有任务统一为文本到文本的格式。例如,在预训练时,T5 会将输入文本进行部分遮蔽,然后要求模型生成被遮蔽的部分(类似于 BERT 的 MLM,但 T5 是整体作为文本输入,输入和输出都是文本)。通过这种方式,T5 学习到文本的生成与理解,并能够处理多种任务(例如翻译、摘要、问答等)。
T5 的一个关键特点是,它采用了统一的输入和输出形式——所有任务都被视为“文本到文本”的问题。因此,T5 的预训练任务包括了多种形式的任务,如填空、翻译、摘要等。
总结:
- BERT:使用 Masked Language Modeling (MLM) 和 Next Sentence Prediction (NSP)。
- GPT:使用 Causal Language Modeling (自回归语言建模)。
- T5:使用 Text-to-Text Transformation (去噪自编码),通过将输入文本进行变换来训练模型。
| 模型 | 使用的 Transformer 部分 | 双向/单向 | Pretext Task | 主要特点 | 據chatgpt說的擅長任務 |
|---|---|---|---|---|---|
| BERT | 编码器(Encoder) | 双向(Bidirectional) — I love playing soccer on the weekend. 用 I love playing 和 on the weekend 預測 soccer |
Masked Language Modeling (MLM),Next Sentence Prediction (NSP) | 只使用编码器,双向理解上下文,适用于理解任务。 | 理解任务:文本分类、命名实体识别、情感分析、自然语言推理等 |
| GPT | 解码器(Decoder) | 单向(Unidirectional) — I love playing → soccer → on → the → weekend |
Causal Language Modeling | 只使用解码器,自回归模型,生成文本。 | 生成任务:文本生成、对话生成、文章续写等 |
| T5 | 编码器 + 解码器(Encoder-Decoder) | 双向/单向(Bidirectional/Unidirectional) — 依任务而定? | Text-to-Text (Denoising Autoencoding) | 结合编码器和解码器,统一文本到文本任务,适用于多任务。 | 多任务:翻译、摘要、问答、文本分类等 |
降維
dimensionality reduction
Autoencoder 和 conv / pooling 都算降維,conv 不光能用大 stride 減小 H, W 維度,還能用 1x1 減少 channel 數。
PCA, t-SNE
跟投影的區別?目标:投影通常是为了将数据映射到一个子空间,并且不一定考虑减少信息损失,除非该投影是最佳的(例如,主成分分析(PCA)中的投影)。
| 特性 | PCA | t-SNE |
|---|---|---|
| 降维类型 | 线性降维 | 非线性降维 |
| 保留的信息 | 保留全局结构(数据的方差) | 保留局部结构(相似数据点的关系) |
| 适用情况 | 适用于线性可分的数据集 | 适用于非线性、复杂的数据集 |
| 可解释性 | 可以通过主成分解释数据的方差 | 不容易解释低维嵌入的含义 |
| 可视化效果 | 更适合全局结构的可视化 | 更适合展示局部结构和聚类效果 |
| 计算复杂度 | 相对较快,适用于大规模数据集 | 计算时间较长,尤其对于大数据集 |
| PyTorch 使用方法 | torch.pca_lowrank() 或通过自定义实现特征值分解 |
from tsnecuda import TSNE TSNE(n_components=2, perplexity=15, learning_rate=10).fit_transform(X), TSNE創建對象fit_transform實現降維 |
| Numpy 使用方法 | np.linalg.svd() 或 np.linalg.eig() |
使用 sklearn.manifold.TSNE(),Numpy 主要用于数据操作 |
| 关键步骤 | 1. 标准化数据(均值为0,方差为1)。 2. 计算协方差矩阵。 3. 计算协方差矩阵的特征值和特征向量。 4. 选择最重要的主成分并将数据投影到这些主成分上。 |
1. 计算高维空间中每对点之间的相似性(通常使用高斯分布)。 2. 在低维空间中随机初始化点的位置。 3. 通过优化算法调整低维点的位置,使得相似点在低维空间中靠得更近。 4. 使用 t-分布(Student’s t-distribution)来计算低维空间中的相似性,并减少拥挤现象。 |
Lecture 19 3D Vision
Assignments
https://cs231n.stanford.edu/assignments.html
assignment 1 和 2 都是做了 2024 版的,3 在這之外會額外做 2017 版的 Visualization 等。
大部分內容(代碼/理論)上面和四年前的博客都已經寫過了,這裡是殘羹剩飯。
CIFAR-10 open-ended challenge
Assignment 2 PyTorch.ipynb 2024 version Part V
Idea 0
- Convolutional layer (with bias) with 32 5x5 filters, with zero-padding of 2 (N x 32 x 32 x 32)
- ReLU
- Convolutional layer (with bias) with 16 3x3 filters, with zero-padding of 1 (N x 16 x 32 x 32)
- ReLU
- Fully-connected layer (with bias) to compute scores for 10 classes
已經 1 個 epoch 就達到了接近 60% 的 accuracy,第一個目標是作業要求的 10 epochs 70%。
Idea 1
簡單地增加模型深度,從 3 layer 變成 4 layer,用 batchnorm 輔助擬合加速收斂。學 AlexNet 先變深後變淺,還是保證維度一樣。
- Convolutional layer (with bias) with 64 5x5 filters, with zero-padding of 2, stride=1 (32x32)
- Batchnorm
- ReLU
- Convolutional layer (with bias) with 32 5x5 filters, with zero-padding of 2, stride=1 (32x32)
- Batchnorm
- ReLU
- Convolutional layer (with bias) with 16 3x3 filters, with zero-padding of 1, stride=1 (32x32)
- Batchnorm
- ReLU
Fully-connected layer (with bias) to compute scores for 10 classes
沒加 batchnorm 只加一層 64 x 3 x 5 x 5 conv 的時候,10 個 epochs 後 acc 無法超過 10%,也許是模型變深導致優化難度變大,如果只是因為其他超參沒跟著一起變,不至於差到這個程度;
- 有的時候不能擬合,有時可以
- 沒加一層 conv,只加 batchnorm 也導致 acc 變成 10%,可能是因為 BN 潛在引入噪聲導致的正則能力讓小模型沒有能力學習了。
- 比上面只加深不 batchnorm 的情況收斂機率稍微高一些,但就算收斂了也比原先 3 層沒有 batchnorm 時效果差。
- 結論是在 3 layer 基礎上加深網絡,且用 batchnorm 輔助收斂,即同時加一層 64 x 3 x 5 x 5 conv 和 batchnorm 的 acc 提高 5% 左右,從不到 60% 變到了 65%。
這裡發現沒圖真不好判斷過擬合等情況,用 pytorch 跟以前一樣存一下 acc_train/val_list 然後畫個曲線:
用了更深層,3-layer to 4-layer,用了更多參數,32 channels to 64 channels,確實有提升,
| 原始的 3 層,只加 batchnorm | 用 4 層,第一層 conv 32 channels | 第一層 64 效果好點有限 |
|---|---|---|
 |
 |
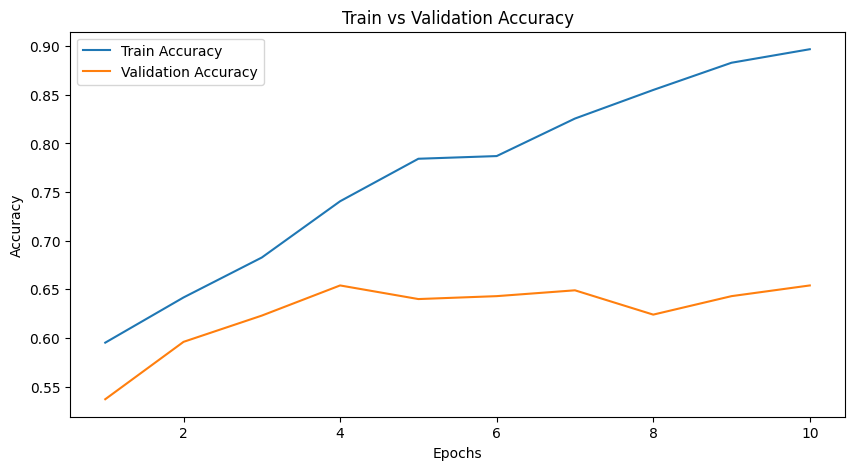 |
Idea 2
發現 train_acc 相比 val_acc 高太多,過擬合嚴重,所以加dropout,如果達不到 70% 的小目標就繼續改架構,如果接近就換 Adam 和 parametric ReLU。
Block0:
Batchnorm - ReLU - Dropout (p=0.2) p 是丟棄概率
- Convolutional layer (with bias) with 64 5x5 filters, with zero-padding of 2, stride=1 (32x32)
- Block0
- Convolutional layer (with bias) with 32 5x5 filters, with zero-padding of 2, stride=1 (32x32)
- Block0
- Convolutional layer (with bias) with 16 3x3 filters, with zero-padding of 1, stride=1 (32x32)
- Block0
- Fully-connected layer (with bias) to compute scores for 10 classes
0.2時還真到70%了,沃草,成就感拉滿,設置到 0.5 試試,0.5 雖然過擬合減輕了,但實際 acc 變差。
| 加 dropout 正則就達到目標了 | 調大正則調多參數效果不太好 |
|---|---|
 |
 |
按計劃,換 prelu 和 adam 1 個 epoch 裡 learning rate 1e-3 比 1e-2 好很多,所以就用 1e-3 懶得調參了。
| dropout 0.2, prelu, adam 1e-3 | dropout 調大 0.5 效果不好,所以一直用 0.2 |
|---|---|
 |
 |
跑完 10 個 epochs 確實又好了一點兒,跟之前自己 from scratch 寫時的經驗情況差不多,換這些技術都有效果提升,至少穩定在 70 以上了,但還是過擬合嚴重,dropout 再次設置到 0.5 還是效果不好,改回 0.2 dropout,發現沒加 L2 正則,用優化器內置的 weight_decay 加 L2 正則:
| 1e-3 L2正則 | 1e-4 L2正則 |
|---|---|
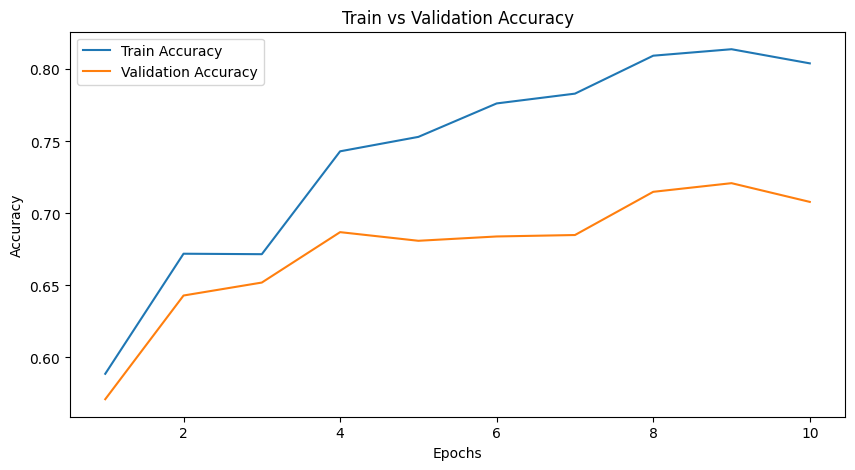 |
 |
先upsampling然後maxpool?圖太小效果未必好,最終結果 acc 是 69.99%…懶得弄了。
Checking accuracy on test set
Got 6999 / 10000 correct (69.99)
0.6999
直接轉實現 resnet、densenet、googlenet、squeeze net 和 visualization。算了暫時不在CIFAR-10上訓了,還是得ImageNet。
COCO
train_captions <class 'numpy.ndarray'> (400135, 17) int32 |
2014 版一共 82783 個 training images 和 40504 個 validation images,原數據共 20 GB,是由 Amazon Mechanical Turk 這個众包平台的全世界工人 Turkers 標注的。
400135 是總的 captions 數,82783 一般每個圖 5 個 captions,有的圖不到 5 個所以小於 82783 x 5 = 431915。
每個 caption 會用 NULL 填充到最長的 17 words,即每個 caption 文本長度是 17。chatgpt 的 max length 是 2048 個 token。idx_to_word 是 '<NULL>', '<START>', '<END>', '<UNK>', 'a' 索引對應 word 的 list,UNK 是 vocabulary 裡沒有的詞的代替 token UNKNOWN。word_to_idx 就是反過來對應索引的 dict。<U63是 Unicode 字符串,且最多包含 63 个字符。比如 train_urls[0] 是 http://farm4.staticflickr.com/3153/2970773875_164f0c0b83_z.jpg 這個圖片。
Colab
# **This mounts your Google Drive to the Colab VM.** |
2022在商汤时跟着卢博用熟了jupyter发现非常方便,只是有的操作会很卡。虽然一年半过去,如今试图回忆往昔只剩脑袋空空,不过再打开colab操作起来还是很舒适自然的。本科时觉得colab跟我全权掌控的小云服务器相比有各种不便,读研实习尝试过vivo网易各个公司的infra后发现各家都是大同小异,就像去哪都要适应新的开发环境一样,colab只是把适应对象从公司的gpu clusters换成google cloud而已。
再看当时跑的cogview和OFA,其实都只是无脑地跑inference。我一直说深度学习是经验科学无迹可寻,只是因为2020、2021年这些assignments里的代码基础我没玩熟练。普通的computer science对我来说其实就像machine learning一样,计算机的底层系统是怎样运行的我也不甚清楚,一句print(“Hello, World”)背后怎么变成字节码?字节码怎么由cpython的c语言逐条执行/解释/转换成汇编指令?汇编指令又怎么变成机器码?机器码又怎么被cpu处理?
这其实跟理解反向传播的计算图一样,没必要每写一个def function():都想清楚cpython在干嘛,没必要每写一个net都想透梯度怎么七十二变,但做哪个任务比如image classification那他的pipeline一定得玩熟,网络的每一个模块是什么作用一定得玩熟。当然可以借助工具,今天我记不起“assert”、“yield”的作用了,记不起Softmax、Batch Normalization的作用了,当然可以查资料,但这都建立在能很快搭一个积木,供尝试Softmax、Batch Normalization的基础上,如果一个最简单任务的pipeline我都没法熟练随手搭建,何谈尝试陌生模块?就好像今天记不起yield的作用,我就必须会写def function():、知道怎么写type()、for-loop才能测试。
Colab Pro
【一个对话框下,不同gpu每小时消耗计算单元的数量】(具体以系统自动计算为准):
T4(大约2个每小时)
A100(大约11.7个每小时)
L4(大约4.8个每小时)
V100(大约6个每小时)
TPU(大约2个每小时)
CPU 0.07h
You are not subscribed.
Available: 99.99 compute units
Usage rate: approximately 0 per hour
You have 0 active sessions.
淘宝用泰铢 47.9 块买了 9.9$ 加 tax 快 80 人民币的 100 个计算资源(比 Colab Pro 稍微划算一些),不知道为什么这么便宜。总之还是比网费便宜多了,而且能督促自己一次写完代码。
能用 V100 和 A100 已经跟在商汤时的资源类似了,在那边我也只是有两张卡和 cluster 能用而已。可能因為充的錢不夠後來發現只能用 A100 不能用 V100。
跑GAN的最後一個效果最好但很深的網絡DCGAN(Deeply Convolutional GANs)時,用2到4核(最多超線程8核)的CPU跑時,等了好幾分鐘跑不出250個iteration,一換上最便宜的2560核T4,相同的時間直接整個把Jupyter都跑完了。也是Pytorch底層優化寫得好吧。
上面跑 assignment 找 better cnn architecture 時兩年來頭一次用上了在商湯時跟大家學到的東西,調架構調參——畫圖——分析實驗結果,感慨。
Regular Expression
写博客写代码时经常会用regex正则批量修改文本,所以在这里记录一些常用的以免重复造轮子。
加粗标题
以此为例,第一行为被替换原文本,第二行为替换后文本。^(#+) ((?!\*)(.*))$1 **$2**
- 先用(pattern)匹配markdown标题井号;
- 然后是个negative lookhead
(?!)匹配井号后没有星号的文本,这里用转义符escape character反斜杠。
图片缩放
markdown图片语法不方便改大小位置,改成html语法的img比较方便操作,写markdown的时候每个都手敲img又太费劲不如![]()。!\[(.*)\]\((.*)\)<img src="$2" loading="lazy" alt="$1" width="50%" height="50%">
or<div align=center><img src="$2" loading="lazy" alt="$1" width="50%" height="50%"></div>
wiki圖片改assets路徑
!\[(.*)\]\(((?!/assets/).*)\)
大小写转换
小写全部换大写:[a-z]\U$0
小知识
- et al(and others in Latin)跟at all读音就是一样滴。
- “Vanilla”常被视为“基本”或“经典”的代表,因为它是最初的冰淇淋和甜品口味之一,且易于与其他味道搭配。这种简单而纯粹的特性使它成为许多食品的基准,从而赋予其“最初”或“标准”的象征意义。
- 他们用的也是google slide(macos)。
- hexo deploy 報錯,解決方案,在blog/node_modules/hexo-deployer-ali-oss/index.js裡修改timeout時間。
[Deployer error] 部署异常[ 文件路径 : /Users/v2beach/code/blog/public/pics/cs231n/Screenshot 2024-11-14 at 01.48.31.png,对象键 : pics/cs231n/Screenshot 2024-11-14 at 01.48.31.png]
Error [ResponseTimeoutError]: Response timeout for 60000ms, please increase the timeout or use multipartDownload.
at Client.requestError (/Users/v2beach/code/blog/node_modules/ali-oss/lib/client.js:311:11)
at Client.request (/Users/v2beach/code/blog/node_modules/ali-oss/lib/client.js:207:22)
at runMicrotasks (<anonymous>)
at processTicksAndRejections (internal/process/task_queues.js:97:5)let result = await client.put(objectKey, localPath, {timeout: 120000});
- hexo d -g通過Node.js上傳到ali OSS會越傳越慢,最後超過默認60s timeout,嘗試multipartUpload還是超時,沒有嘗試流式上傳,只能修改timout到2分鐘。
hexo在config.yml裡註冊新配置:图太多不能再塞了,打开这篇文章得加载个大几分钟。hexo.extend.deployer.register('ali-oss', function(args){
- chatgpt公式prompt:
里面的\[\]和\(\)都换成dollar符号。 - x~p(x) 讀作 x follows the distribution p of x,或者 x follows p of x。
常遇見bug一覽
1. 求梯度dW寫成dw或者反之,非常難查出來。
2. np.max和np.maximum不一樣。
| 功能 | np.max |
np.maximum |
|---|---|---|
| 作用 | 计算数组的全局最大值或按指定轴计算最大值 | 逐元素比较两个输入,返回对应元素的最大值 |
| 输入 | 单个数组,可选 axis 参数 |
两个数组或一个数组和一个标量 |
| 输出 | 标量(全局最大值)或数组(按轴最大值) | 与输入形状相同的数组 |
| 广播支持 | 不支持广播 | 支持广播 |
3. 總算知道數據穩定啥意思了,比如/zero和exp溢出,所以BN和數值穩定版softmax或者其他穩定技巧才重要。
(Iteration 1 / 125) loss: 7.856643 |
梯度爆炸。為什麼這裡loss不顯示Inf而顯示nan?因為exp產生的infinity在後續任何計算——比如inf-inf或0*inf,都是無效操作結果為nan。print(np.inf-np.inf, 0*np.inf, 1*np.inf)
nan nan inf
| 特性 | NaN | Inf |
|---|---|---|
| 含義 | 無效或未定義值 | 超出數值範圍的值 |
| 來源 | $0/0$, $\sqrt{-1}$ | $1/0$, $10^{309}$ |
| 比較行為 | 與任何數值比較均為 $False$ | 可以比較大小 |
| 檢測方法 | np.isnan() |
np.isinf() |
直接将 $ \log\left(\frac{\text{up}}{\text{down}}\right) $ 改写为 $ \log(\text{up}) - \log(\text{down}) $ 不会缓解数值问题,反而可能引入新的风险。
从数值稳定性的角度,$ \log\left(\frac{\text{up}}{\text{down}}\right) $ 中的分数计算可以通过硬件或软件优化,避免极端情况下的下溢问题。
而将其分开为 $ \log(\text{up}) - \log(\text{down}) $ 时:
- $ \log(\text{up}) $ 和 $ \log(\text{down}) $ 会单独计算,可能分别触发下溢或溢出。
两个独立的结果再相减,可能引入额外的浮点数误差。
加 epsilon
- 在求对数前,为分子和分母添加一个小值 $ \epsilon $,避免 0 的出现:
- 通常,$ \epsilon $ 的值为 $ 10^{-12} $ 或 $ 10^{-8} $。
- 最常用數值穩定版本的 softmax:在dropout用500個數據過擬合500層的實驗裡,上面的梯度爆炸問題靠+1e-8沒能解決,因為不是divided by 0,是exp大數,就算沒溢出也會梯度爆炸導致w起飛,必須用數值穩定的softmax減掉xmax。
weight scale?和ass2的其他問題
N, C, H, W = 2, 3, 4, 5 |
4. 參數順序
首先,有默認值的參數 (default argument) 必須在沒有默認值的參數 (non-default argument) 之後。def train(model, optimizer, epochs=1, train_acc, val_acc):
SyntaxError: non-default argument follows default argument
其次,關鍵字參數 (positional argument) 必須出現在位置參數 (keyword argument) 之後。best_model = train(model, optimizer, epochs=10, train_acc, val_acc)
SyntaxError: positional argument follows keyword argument
5. 路徑最好不要有%
圖片路徑加百分號會跟 %20(空格)之類的衝突,報錯URIError: URI malformed。
6. RuntimeError: a leaf Variable that requires grad is being used in an in-place operation.
copy_
= +
+=?
7. markdown 裡 <div></div> 前後要空行,否則會渲染錯誤。
8. Masked self-attention,mask要加在alignment scores變成-inf,只把attention weights置0不行,而且要看明白mask=0代表遮掩還是mask=True代表遮掩。
這次完成得這麼順利:
- 放棄本地配環境,用 colab 或者公司 infra 就是爽,實習得到的經驗;
- chatgpt 查語法比查 document 方便多了;
- 不再追求逐行看懂,全寫完才回頭搞懂一部分內容。
三年前要不是買了 m1,繼續用原來的 windows 可能早就完成了,奈何當時環境兼容性差到幾乎任何一個庫都不能順利安裝。
沒過多久就遇到直到現在都難以承受的變故,又碰到個極品老闆,組裡三個博士全部鬧掰換導師。
當時靠自己實在無法重拾信心,這一年多虧朋友、女友。時也,命也。
一旦国家机器被用来维护特定阶级的利益,它就会成为腐败的工具,即便这个阶级声称是无产阶级。
