2025-3-19
写 SSL 协议这篇博客时写到了 C++ 的 unordered_map 用的是 FNV 哈希,算是除了当年分析排序算法之外第一次试图理解 STL 的底层实现,让我回忆起 2022 年的 3 月 (25号~9月18号),在残酷刷题群里麻木刷题时不懂底层道理只会调用 STL 的难受。在等待训练 chemprop 作为 molgen 奖励函数的时候,重新调通三年没碰的 macOS vscode cpp 工作流,试着借助 chatgpt 搞懂 STL 容器。
vector
vector 底层实现:动态数组(dynamic array,连续内存快)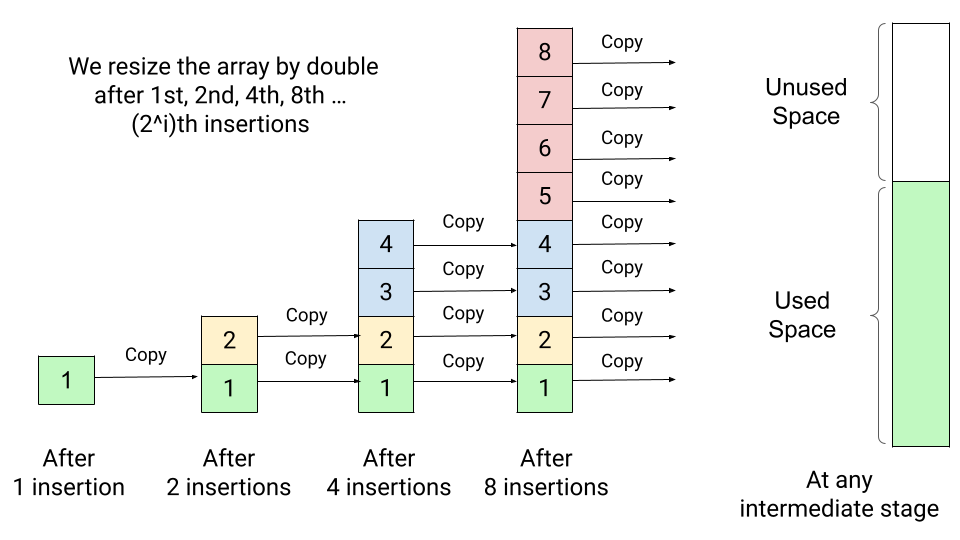
C++ 的 std::vector、Java 的 ArrayList、Python 的 list 都是动态数组的实现,数组的元素在内存中是连续存储的。
时间复杂度:
- 读写:O(1),内存中连续存储所以支持快速随机访问。
- 增删:如图所示,在元素占满数组时会开两倍内存,并把内容复制过去。O(n)。若不满:
- 尾部插入删除:O(1)。
- 中间或前部插入删除:O(n),保持内存连续。
list
list 底层实现:双向链表(doubly linked list)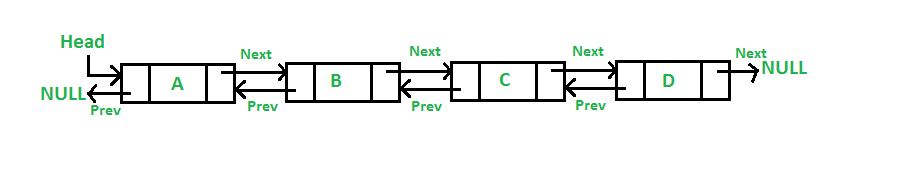
C++ 的 std::list、Java 的 java.util.LinkedList、Python 的 collections.deque(下文讲) 都是双向链表的实现。如图每个结点比单向链表多维护一个 prev 指针,因此在 O(1) 的时间内可以获取前驱结点,进而加速了插入和删除操作。
| 操作 | 时间复杂度 | 说明 |
|---|---|---|
| 读写 | 由于链表不支持随机访问,必须从头或尾部遍历到目标位置 | |
| 头部插入删除(Insert or Delete at Head) | 直接修改 head 指针,不需要遍历 |
|
| 尾部插入删除(Insert or Delete at Tail) | 直接修改 tail 指针,不需要遍历 |
|
| 中间插入删除(Insert or Delete at Index k) | 需要遍历到索引 ,然后插入或删除 |
deque
deque, double-ended queue, 双端队列。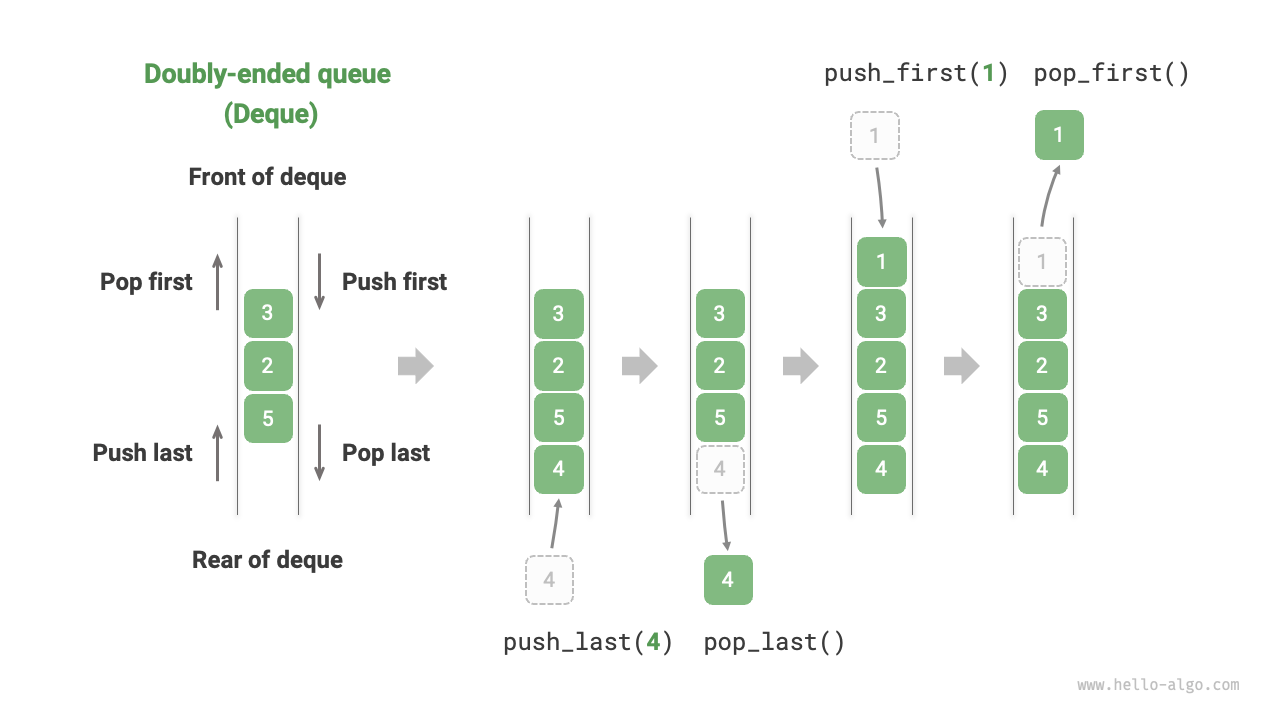
C++:std::deque(动态数组实现,写到这才发现有官方文档:https://cplusplus.com/reference/deque/ ),Java:ArrayDeque(动态数组实现)、LinkedList(实现了 Deque 接口,双向链表实现),Python:collections.deque(双向链表实现)。
着重讲一下 deque,因为 C++ 和 python 的 stack 和 queue 都是用 deque 实现的。在 C++ 里管 stack 和 queue 叫 Adaptors(适配器),指的是不直接存储数据,用已有容器(underlying container)提供新的接口,使其行为满足特定需求的特殊容器;在 python 里管 deques 叫做 stacks 和 queues 们的泛化(generalization)。
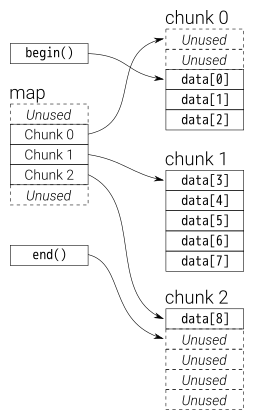
C++ 的 deque:分块(chunks)存储,每个内存块chunk都是定长的vector,用一个指针队列(map,如图所示)管理这些内存块,保持物理不连续但逻辑连续,map本身也是一个vector。deque跟vector有些像,内部结构稍微复杂一些,在存非常长的序列时deque会更高效地扩展,因为vector此时重新分配内存(reallocation, O(n))会开销很大。
这篇文章gif失效了。
在 Python 里 deque 是用双向链表串连起内存块。3.8.1的源码在这。与之类似的 list(是C语言优化的指针数组)在增删头部(pop(0) 或 insert(0, v))时有 O(n) 的内存移动成本,但对固定长度的快速操作做了优化。
stack
LIFO (last-in first-out)
C++有std::stack(deque的adaptor)Java有Stack<E>(Java的栈顶叫peek,C++和Python都叫top),Python里可以用list、deque模拟。
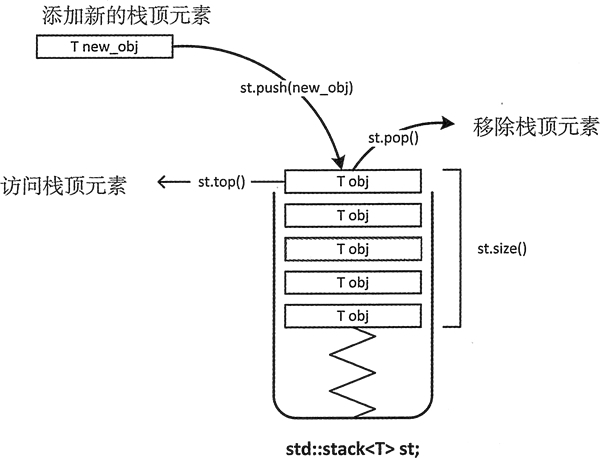
| 操作 | 时间复杂度 |
|---|---|
入栈 (push) |
|
出栈 (pop) |
|
访问栈顶 (top/peek) |
|
查找 (search) |
queue
FIFO (first-in first-out)
C++有std::queue(deque的adaptor),Java有Queue<E>,Python里提供了线程安全的队列实现。
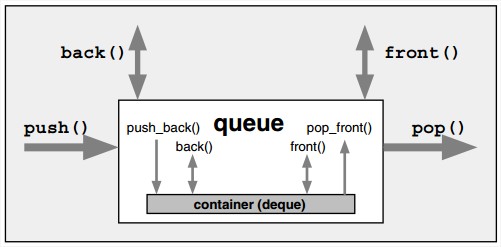
| 操作 | 时间复杂度 |
|---|---|
入队 (enqueue) |
|
出队 (dequeue) |
|
访问队首 (front) |
|
查找 (search) |
priority_queue
priority_queue是大根堆,即每个结点的值都小于等于其父结点,堆是一棵树。
大根堆主要支持的操作有:插入一个数、查询最大值、删除最大值、合并两个堆、减小一个元素的值。
可并堆支持高效合并。
可持久化,是对任意历史版本进行查询或者操作,产生新的版本。
priority_queue往往是二叉堆,提到堆也往往指二叉堆。
下表来自oi-wiki,oi-wiki 对下面三个数据结构解释得都不错,建议直接看oi-wiki,这里只作为笔记。
操作 \ 数据结构 |
二叉堆 | 配对堆 | 左偏树 | 二项堆 | 斐波那契堆 |
|---|---|---|---|---|---|
| 插入(insert) | $O(\log n)$ | $O(1)$ | $O(\log n)$ | $O(\log n)$ | $O(1)$ |
| 查询最大值(find-max) | $O(1)$ | $O(1)$ | $O(1)$ | $O(1)$ | $O(1)$ |
| 删除最大值(delete-max) | $O(\log n)$ | $O(\log n)$ | $O(\log n)$ | $O(\log n)$ | $O(\log n)$ |
| 合并 (merge) | $O(n)$ | $O(1)$ | $O(\log n)$ | $O(\log n)$ | $O(1)$ |
| 减小一个元素的值 (decrease-key) | $O(\log n)$ | $o(\log n)$(下界 $\Omega(\log \log n)$,上界 $O(2^{2\sqrt{\log \log n}})$) | $O(\log n)$ | $O(\log n)$ | $O(1)$ |
| 是否支持可持久化 | $\checkmark$ | $\times$ | $\checkmark$ | $\checkmark$ | $\times$ |
increase key呢?
详细复习一下七年前学的二叉堆和二叉搜索树:
Why is Binary Heap is better than BST for Priority Queue?
What is the underlying data structure of a STL set in C++?
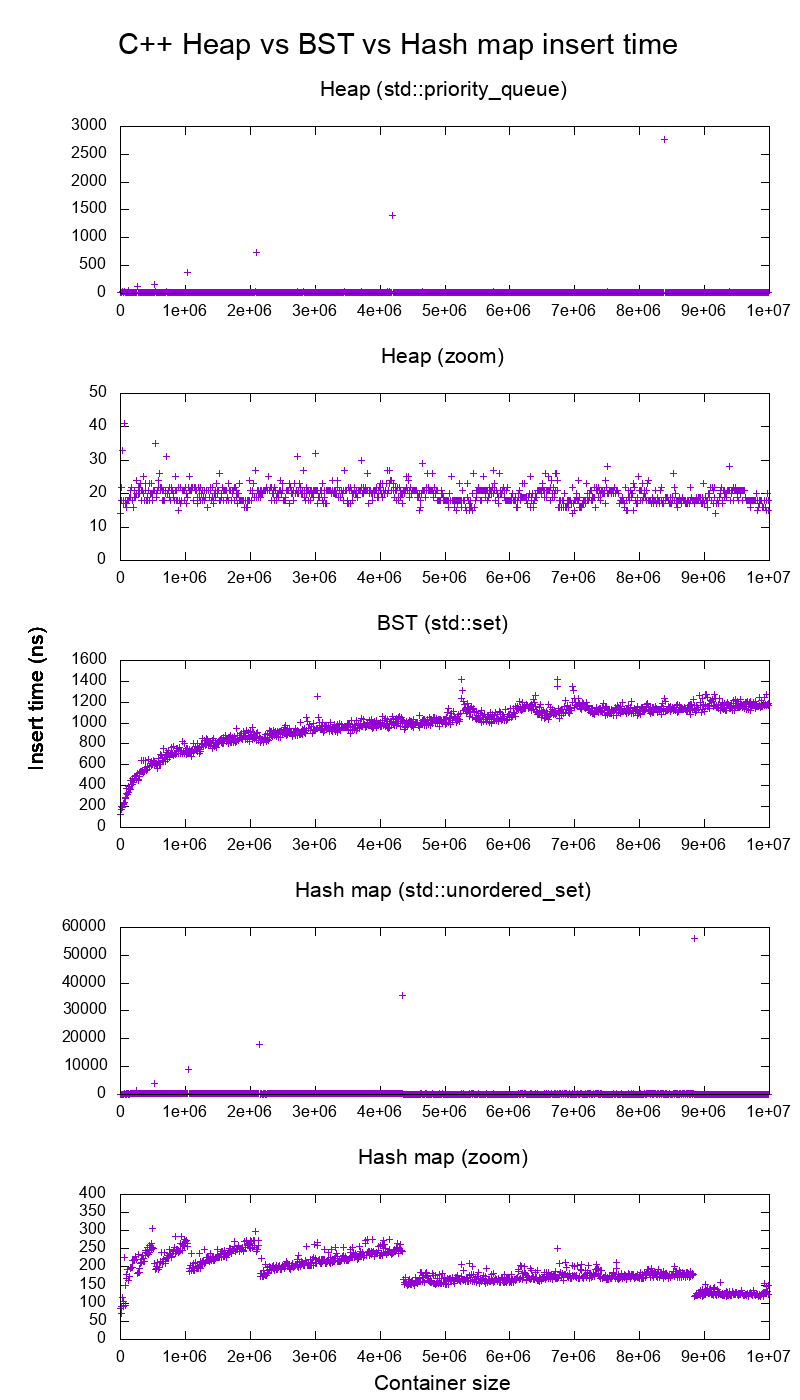
玩熟练这下面这仨复杂高效的 STL 容器的数据结构(二叉堆、二叉搜索树(→二叉平衡树→红黑树)、哈希桶)基本就对算法题的数据结构得心应手了吧。
二叉堆Binary Heap
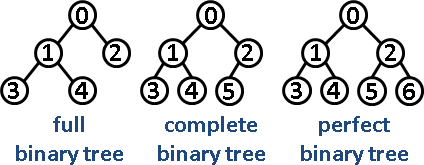
二叉搜索树Binary Search Tree
map
红黑树
unordered_map
哈希表
set
红黑树
unordered_set
哈希表
附图
肄业倒计时
今天交完房租,结束了在这个出租屋的第 25 个月。感谢邻居早 8 点准时响起的电钻,把我赶来北街咖啡,赶来大食堂。无论是以前还是现在,在家里一个人呆着只会让我腐烂发臭,turn into the Rotten of Black Gulch。
肄业(yì yè, Dropping Out),肆业(sì yè, 勤于所业)。根据汉典,肄的意思有:「肄,習也。」「肄,嫩條也。」「肄,勞也。」算是个“退学”的仁慈版本。
By all means marry. If you get a good wife, you’ll be happy. If you get a bad one, you’ll become a philosopher. (Socrates,苏格拉底有个好老婆还是坏老婆呢)
